随机波浪中张力腿平台耦合运动及系泊系统特性研究
谷家扬,吕海宁,杨建民
(1.上海交通大学海洋工程国家重点试验室,上海 200240;2.江苏科技大学船舶与海洋工程学院,江苏镇江 212003)
随机波浪中张力腿平台耦合运动及系泊系统特性研究
谷家扬1,2,吕海宁1,杨建民1
(1.上海交通大学海洋工程国家重点试验室,上海 200240;2.江苏科技大学船舶与海洋工程学院,江苏镇江 212003)
张力腿平台(TLP)是一种垂直系泊的半顺应半刚度式平台,预报平台的运动响应及锚泊系统的张力是张力腿平台结构设计的重要基础。应用挪威船级社SESAM软件在频域和时域内研究了张力腿平台在随机波浪中的非线性运动响应及系泊系统特性,并在试验室中通过缩尺比为1∶40的模型进行了试验验证。在试验验证的基础上,将仅考虑浪与考虑浪、流联合作用下的张力腿的张力平均值、幅值及标准差作了对比。结果表明,在较低海况时,考虑浪和流时的张力腿与不考虑流的情况变化不大;在较大海况时,流的影响不可忽略,考虑流的张力腿变化幅度要略大于不考虑流的情况。
张力腿平台;动力响应;随机波;系泊特性
随着世界深水油气田的不断发展和开发,传统的导管架平台已经不能满足深水海域,取而代之的是各种新型浮式平台,如顺应塔平台、张力腿平台、SPAR平台、半潜平台、FPSO、PDPSO等。张力腿平台(TLP)是一种垂直系泊的半顺应半刚度式平台,平台包括四大部分:平台、锚泊系统(张力腿)、平台基础、海底立管。起重平台部分由船体和上部甲板组成,船体部分又由立柱和浮箱组成。张力腿系统是由多组绷紧的钢质缆索组成,其组数亦与平台上体的形状有关,每组缆索又由若干根钢索或钢筋束构成,下端直接固定在锚固基础上,其内产生的张力与平台的剩余浮力相平衡。系泊方式主要为顺斜系泊和垂直系泊两种。张力腿系统不仅控制着平台与井口相对位置,还对其安全性起着决定性作用。
对张力腿平台的运动响应大部分研究都是基于时域分析。S Ahmad[1]研究了TLP在随机波海浪谱下的耦合响应。考虑了水动拖曳力,可变张力,可变浸水、长期偏移和波动风载荷耦合效果引起的各种非线性效应。S Chandrasekaran等[2]研究了随机波载荷下三角形TLP的动态响应。对六个自由度响应进行了谱分析得出响应规律,同时考虑耦合、可变浸水以及流的影响。Tabeshpour等[3]在时域和频域中对TLP进行了非线性动态分析,随机波的时间历程基于PM谱,随机波以任意浪向角作用在结构上。A K Jain[4]采用确定性的一阶波浪力来分析TLP的动态响应,考虑6自由度的耦合、非线性的张力变化及水动力的影响。S Chandrasekaran[5]采用了相同的计算理论,数值计算比较了三角形和四边形TLP的耦合响应以及不同参数对TLP运动响应的影响。曾晓辉等[6]论证了张力腿平台在波浪作用下发生有限振幅运动时,所受惯性力、粘性力、浮力等荷载以及张力不仅与波浪有关,还与瞬时响应有关,是响应的非线性函数。上述研究有一个共性,波浪荷载均采用改进的Mrison公式进行研究,而TLP立柱和浮箱都属于大直径结构,这样的简化处理必然会引起张力腿平台外部波浪荷载的计算误差。此外中科院力学所刘玉标[7]等利用WAMIT软件,计算了某多柱式张力腿平台的艏摇幅值及水平方向响应的极大值。“典型深水平台概念设计研究”课题组[8]以1 000 m水深TLP平台为例,详细叙述了TLP平台水动力分析的过程和方法,包括有限元模型的建立,水动力特征的计算,水动力载荷响应的计算以及运动响应分析。
以一座500 m水深的TLP为研究对象,对不同海况下的动力响应进行了数值计算,并将数值模拟的结果与试验室风浪流水池中的试验结果进行对比分析,探索了不同海况下运动响应及系泊特性的规律。
1 计算理论
1.1 浮式结构物的运动方程
对于浮式海洋结构物来说,耦合分析是考虑结构物主体和系泊系统的相互影响,建立整个系统的运动方程和动力方程进行求解的过程,是一类复杂的非线性问题,考虑系泊系统的回复力、阻尼力和惯性力对结构物主题的平均位置以及动力响应所产生的影响。
考虑各种载荷下,张力腿平台的谐振运动方程可以表示为

式中:M为与频率有关的质量矩阵,包含结构物质量矩阵m和与频率有关的附加质量矩阵A;C为与频率有关的势流阻尼矩阵;D1,D2为线性阻尼和二次阻尼矩阵;f为速度矢量函数,可表示为fi=˙xi|˙xi|;K为与位置有关的静水刚度矩阵;x为位移矢量;q为激励力矢量。
右边项的激励力可以表示为
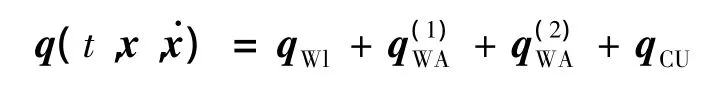
式中:qWI为风载荷为表示一阶和二阶波浪激励力;qCU为流载荷。
1.2 运动方程的分解
在通过时延函数求解时历微分方程式时,通常将运动分解为由一阶波浪力(高频部分)和二阶波浪力(低频部分)引起的两部分。有两种近似计算二阶波浪力(低频部分)的方法:一是Hsu和Blenkan基于窄带假设的波浪谱;另一种就是通过Newman基于一些假设得到的二阶传递函数来计算。这里主要用到第二种方法。
高频部分可以在频域内求解,通常要求运动为波浪的线性响应,这就意味着二阶阻尼D2为零,同时刚度K恒定。
激励力也分为一个高频的部分q(1)和低频的部分q(2)。

位移矢量可以分解为

频域内求解的高频运动可以表示为

式中:H1(ω)为波面升高同激励力的一阶传递函数。
低频运动可以通过时域内的动态平衡方程求解

2 TLP参数及工况
研究四边形张力腿平台。此平台由四个方形浮筒和四个方形浮箱组成,主尺度如表1。
图1为张力腿平台的俯视图,图中列出了平台的具体尺寸,张力腿及立管的具体编号,张力腿的编号为Tendon1~Tendon8,立管的编号为Riser1~Riser4。
仅考虑波浪时的数值模拟和模型试验主要选择8种典型工况,考虑了不同波高、浪向及周期的影响,具体的环境参数如表2所示。
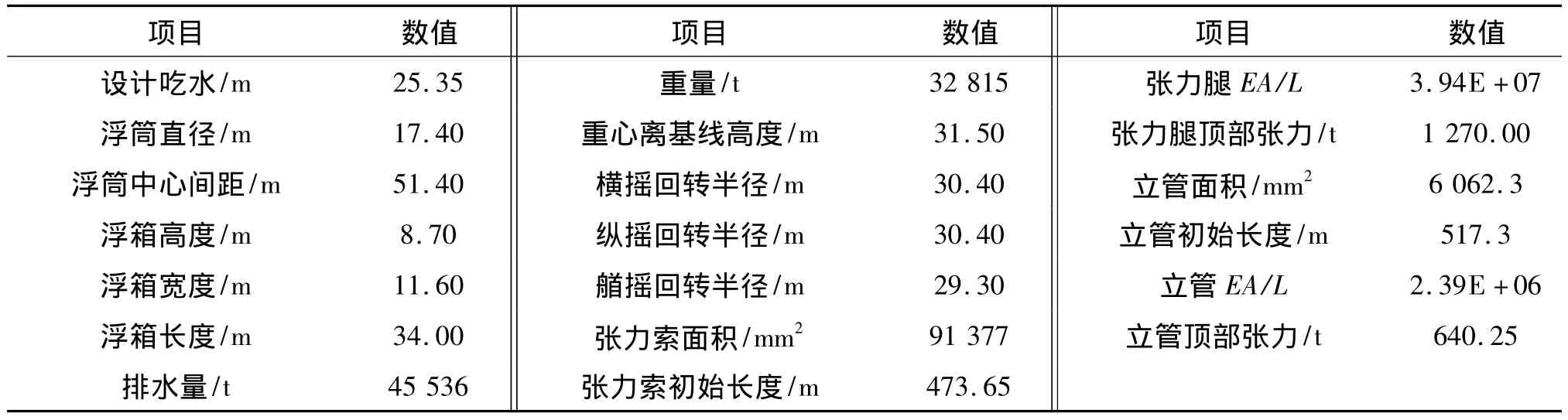
表1 四边形张力腿平台尺寸Tab.1 Main parameters of quadrilateral tension leg platform

表2 工况选择Tab.2 Load case
3 模型试验
为了对数值模拟的结果进行验证,在上海交通大学海洋工程国家重点试验室的风浪流水池中进行模型试验。水池尺寸为50 m×40 m×10 m(长×宽×深),深井40 m。模型试验中采用的浪高与实际的比例为1∶40。采用挂砝码的方式模拟流速,用绳子的拉力代替风力。模型试验的内容包括静水中自由衰减试验,用于计算各方向的无因次阻尼系数和固有周期,随机波浪试验,用以获取典型工况下各自由度的响应谱和相关统计值。
根据静水衰减试验结果,TLP平台在作业吃水时的纵荡、横荡和垂荡固有周期分别为102.4 s、104.5 s、2.76 s;横摇、纵摇和艏摇固有周期分别为 2.37 s、2.32 s、75.4 s。相应的固有频率分别为0.061、0.060、2.276、2.651、2.708 及 0.083 rad/s。

图1 张力腿平台尺寸以及张力腿和立管坐标Fig.1 Dimensions of TLP and the coordinates of tendons and risers
4 数值计算与模型试验对比
4.1 运动响应RAO
将在Patranpre中建成的数值模型导入三维绕射/辐射软件SESAM/HydroD中,在频域中计算得出一系列的水动力系数,包括附加质量系数、势流阻尼系数,以及一阶波浪力、二阶波浪力和运动的频率响应函数。数值模拟了270°浪向下横荡、垂荡及横摇自由度的幅值响应算子,并与模型试验结果进行对比,如图2所示,两者吻合良好。

图2 270°浪向下平台RAO数值计算与试验结果对比Fig.2 TLP RAO comparison between experiment and numerical calculation
4.2 仅考虑浪时的时间历程曲线及统计值
采用SESAM/DEEPC软件分析计算TLP在随机波浪中的耦合运动,软件包括计算浮体响应程序SIMO和计算细长单元程序RIFLEX。SESAM/DEEPC软件在时域计算过程中将TLP本体和张力腿系统耦合起来进行分析,用于实现各时间步下本体和张力腿系泊系统的动平衡。
在数值模拟中,其波浪谱采用现场实际测量得出的波谱,波浪谱为JONSWAP谱。如图3所示。其频率间隔Δω=0.15 rad/s,运动方程计算的时间步长Δt=1 s,共计算 10 800 s。
图4为浪向角315°,波高5 m,周期10.7 s下数模模拟和模型试验的时间历程曲线的对比。从图中可以看出,数值模拟和试验的时间历程基本吻合。表3为该工况下各自由度响应的统计结果。从图中可以看出纵荡、横荡响应远远大于垂荡响应,纵荡响应最小值为-2 m左右,最大值为7 m左右,垂荡运动的无论是数值模拟还是模型试验都不到0.08 m。横摇和纵摇响应在平衡位置附近振荡,幅值在0.1°左右,而艏摇的模型试验室略大,约为0.6°。

图3 计算中所采用波谱Fig.3 Spectrum used in the computation

图4 平台时间历程数值模拟和试验结果对比Fig.4 Time history of TLP between experiment and numerical calculation
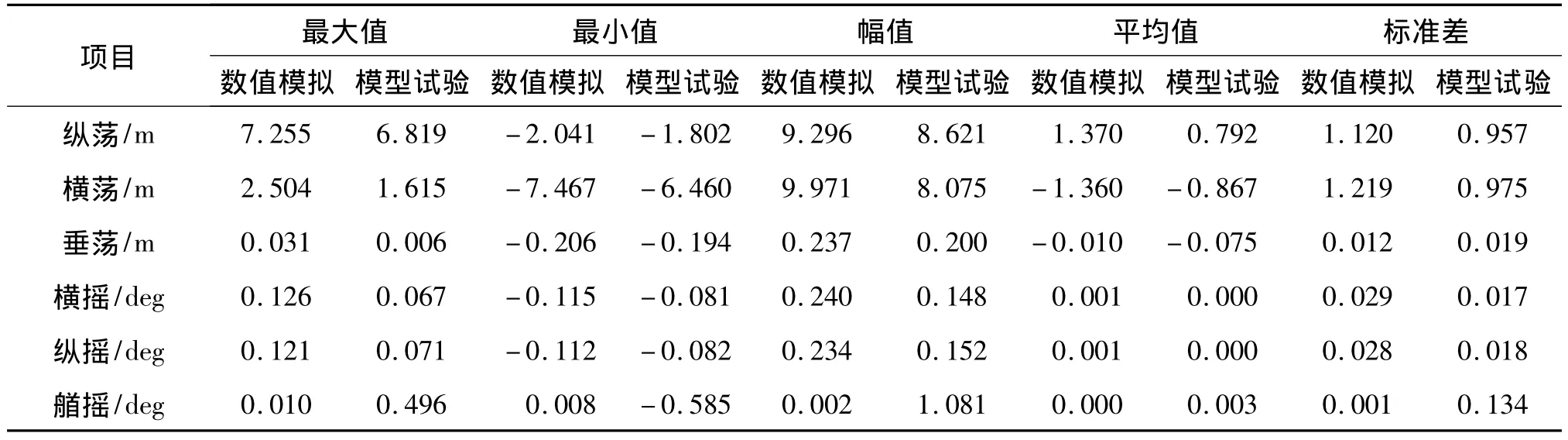
表3 平台动力响应统计(H5)Tab.3 Dynamical statistics of TLP of H5
4.3 张力腿系泊系统特性
限于篇幅,仅列出了315°浪向下H5工况Tendon5~Tendon8张力腿的受力统计,见表4,数值模拟和模型试验的结果基本吻合。图5为Tendon6张力腿的张力历程曲线,试验的平均值在1 250 kN附近,而数值模拟的平均值在1 200 kN左右,两者预报的结果非常接近,误差仅为4%。将该工况的时间历程响应能量谱的计算结果与试验结果进行比较,如图6所示,无论张力腿张力谱的峰值出现的位置和峰值大小,都基本相同,差异不是很大。

图5 张力腿张力历程曲线Fig.5 Time history of the tension for NO.6 tendon

图6 张力腿张力谱Fig.6 Comparison of tension spectrum for NO.6 tendon

表4 张力腿受力统计值(315°,H5工况)Tab.4 Tension statistics of TLP of H5 for 315 degree wave approach
模型试验和数值模拟的对比结果表明,数值模拟的结果有一定的准确性,基本可满足工程计算分析的需要,为进一步研究不同工况及浪向对张力腿平台系泊特性的影响,考虑到本平台的对称性,因此分为0°、22.5°、45°三个浪向,H3~H9七个不同的波高共计21种工况,对#6张力腿的受力特性进行了数值模拟及对比(见图7,表5)。对比结果表明,在相同浪向角下,随着波高的增大张力腿受力的最大值不断增大,而最小值在不断减小,最大值递增幅度为10%不到(最小值递减10%不到)。在相同的波高下,张力腿的张力最大值随浪向角增大而增大,最小值趋势相反。图8为不同浪向及波高下张力腿张力平均值趋势图。
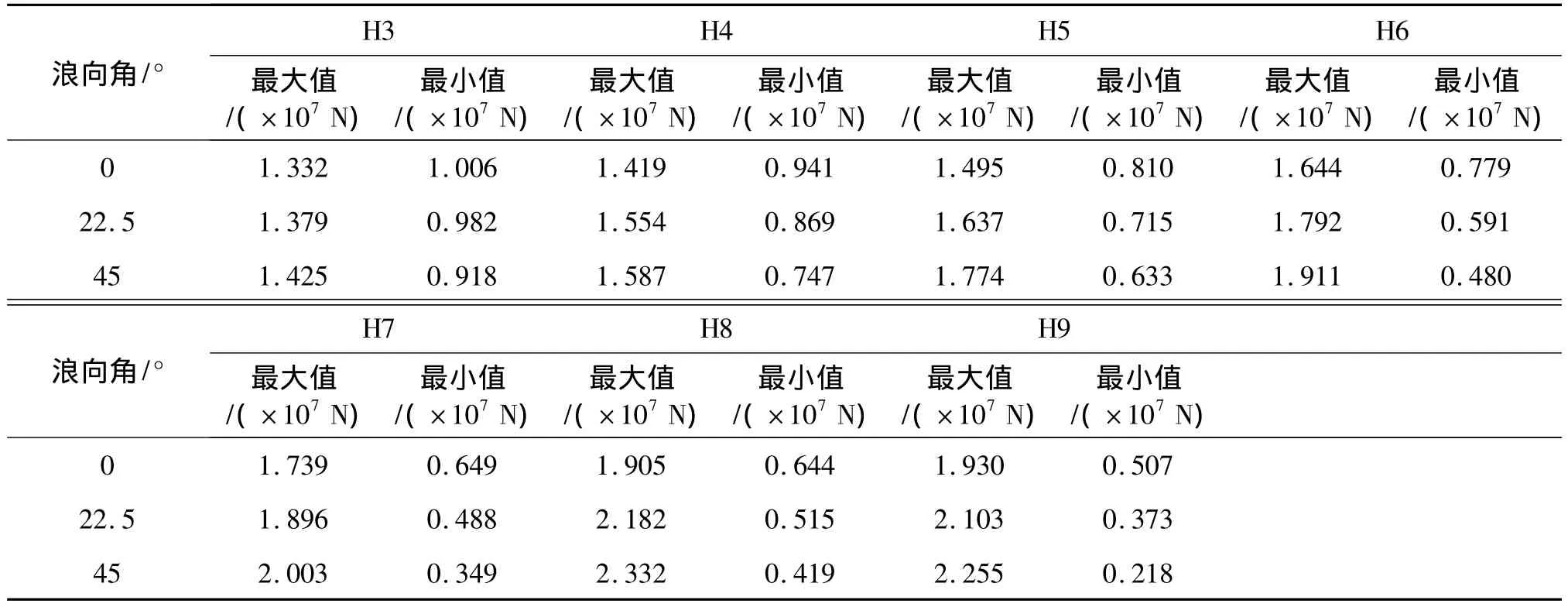
表5 不同波高和浪向下张力腿受力统计值(Tendon6张力腿)Tab.5 Tension statistics of TLP of different wave heights and wave approaches

图7 22.5°四种不同波高条件下平台的张力PSDFig.7 Tension spectrum of different wave heights

图8 不同波高、不同浪向下张力腿平均受力曲线Fig.14 Mean tension of tendon for different wave heights and wave approaches
4.4 考虑浪和浪、流联合作用下TLP张力的影响
为了研究流对张力腿张力的影响,仅考虑浪以及同时考虑浪、流的张力腿张力统计值以及张力能量谱。比较了两种海况,一种为作业海况5,浪向角为22.5°,特征波高5.0 m,谱峰周期10.7 s;另一种为极限海况9,浪向角为 22.5°,特征波高 8.8 m,谱峰周期 14.2 s。流剖面的参数如表 6。

表6 流速分布Tab.6 Vertical current velocity profiles
通过海况5的比较可以发现,流对张力腿张力的影响不大,张力腿的变化幅度略有增大,但当海况增大到9级时,流的影响不可忽略(见图9、10)。

图9 海况5考虑流与不考虑流各个张力腿比较Fig.9 Standard deviation comparison of tendon tension in sea state 5(22.5°)

图10 海况9考虑流与不考虑流各个张力腿比较Fig.10 Standard deviation comparison of tendon tension in sea state 9(22.5°)
5 结语
采用时域与频域分析方法,对一座张力腿平台及其系泊系统的动力响应及系泊特性进行了数值模拟,通过与1∶40的模型试验对比,表明采用的数值模拟方法是合理可靠的,得出如下结论:
1)在仅考虑浪时,浪向和波高对张力腿张力平均值的影响不是很明显,在H3~H9工况中平均值的变化从11.7~11.8 MN变化,但最大值随波高和浪向角的增大而增大,最小值随之减小。
2)随着波浪谱峰周期的变化,张力腿张力谱的峰值频率也发生了变化,在H3、H5、H7、H9随着海况的增大,张力谱的频率从0.35 Hz变化到0.75 Hz,张力谱的谱峰值不断减小,张力谱逐渐远离波浪频率。
3)在较低海况时,考虑浪和流时的张力腿变化情况与不考虑流的影响变化不大;在较大海况时,流的影响不可忽略,考虑流的张力腿变化幅度要略大于不考虑流的情况。
[1]Ahmad S,Islam N,Ali A.Wind-induced response of a tension leg platform[J].Journal of Wind Engineering and Industrial Aerodynamics,1997,72:225-240.
[2]Chandrasekaran S,Jain A K.Triangular configuration tension leg platform behavior under random sea wave loads[J].Ocean Engineeing,2002,29:1895-1928.
[3]Tabeshpour M R,Golafshani A A,Seif M S.Comprehensive study on the result of tension leg platform response in random sea[J].Journal of Zhejiang University:SCIENCE A,2006,7(8):1305-1317.
[4]Jain A K.Nonlinear coupled reponse of offshore tension leg platforms to regular wave forces[J].Ocean Engineering,1997,24(7):557-592.
[5]Chandrasekaran S,Jain A K,Anupam Gupta.Influence of wave approach angle on TLP’s response[J].Ocean Engineering,2007,34:1322-1327.
[6]曾晓辉,沈晓鹏,刘 洋,等.考虑多种非线性因素的张力腿平台动力响应[J].海洋工程,2006,24(2):82-88.
[7]刘玉标,袁文全,申仲翰.迎浪角及波浪周期对张力腿平台响应的影响分析[J].中国海洋平台,2008,23(6):22-25.
[8]“典型深水平台概念设计研究”课题组.张力腿平台水动力响应分析[J].中国造船,2005,46(增刊):477-489.
Studies on coupling dynamic response and characteristics of mooring system of TLP in stochastic waves
GU Jia-yang1,2,LV Hai-ning1,YANG Jian-min1
(1.State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;2.School of Naval Architecture and Marine Engineering,Jiangsu University of Science and Technology,Zhenjiang 212003,China)
Tension Leg Platform(TLP)is a vertically moored semi compliant and semi stiff offshore structure.Predicting the dynamical response and characteristics of mooring system is the important base of the design of tension leg platform.The nonlinear dynamic response and characteristics of mooring system of TLP are studied in frequency domain and time domain under stochastic waves using the software of SESAM developed by the DNV classification society.The TLP model scale of the target structure in the State Key Laboratory of Ocean Engineering of Shanghai Jiao Tong University is selected as 1/40.The results of experiment are compared with the numerical simulations.The amplitude value,average value and standard deviation considering the influence of the current are compared with those not considering the current based on the verification of the experiment.
tension leg platform;dynamic response;stochastic waves;characteristics of mooring system
P751;U661.1
A
1005-9865(2012)04-0042-07
2011-12-02
国家自然科学研究基金(40906049);中海油-上海交大深水工程技术研究中心课题资助项目
谷家扬(1979-),男,江苏扬州人,博士生,主要从事海洋结构物动力响应预报及水动力性能研究。
吕海宁。E-mail:haining@sjtu.edu.cn

