破碎波群间隔统计分布

田文婧，类淑河，管长龙，马海燕，薛 川

(1.中国海洋大学数学系，山东青岛 266100;2.中国海洋大学物理海洋实验室，山东青岛 266100)

破碎波群间隔统计分布

田文婧1，类淑河1，管长龙2，马海燕1，薛 川1

(1.中国海洋大学数学系，山东青岛 266100;2.中国海洋大学物理海洋实验室，山东青岛 266100)

基于一系列实验室风浪破碎实验，讨论破碎波群间隔的统计分布。实验时风速分别设定在6～9 m/s间几个不同的风速水平，破碎波群间隔定义为两个相继发生破碎的波群中破碎首发时刻之间的时间间隔，破碎依据波面信号和实验者同步记录的破碎标记信号判别，分布拟合检验采用Kolmogorov-Smirnov检验。数据分析结果表明:1)所有实验信号的破碎波群间隔都服从Gamma分布;2)低风速情形的破碎波群间隔大多服从指数分布——Gamma分布的一种特殊情形;3)相同实验条件下的破碎波群间隔具有相同的分布。这意味着破碎波群的发生可以视为一种更新过程。

风浪破碎;波群;破碎波群间隔;Gamma分布;更新过程

风浪的群发性是风浪场的重要特性。波群的形成以及它的特征与许多海洋问题有关，特别是与海岸和海洋工程有着密切的关系，波群的出现有时会对海上船只、建筑物、海岸防护堤以及近岸建筑等造成严重的损害［1-4］。

关注波群的另一个重要原因是它与破碎波的发生也密切相关。Donelan［5］等人最早讨论海上白冠破碎的群发性;Holthuijsen and Herbers［6］指出破碎明显受波群影响，他们的观测中有1/3的波群中包含破碎波，70%的破碎发生在波群中。

破碎波群的发生率是衡量波群破碎状况的一个基本指标，它定义为单位时间内发生的破碎波群的个数。目前关于这一指标的研究很少，破碎发生的频繁程度更多地基于单个波定义，比如常用的破碎频率、破碎概率［7-9］。Babanin［10］指出破碎应该视为波群的行为，一个波群内相继发生的破碎可以看作是一次破碎事件，给出了波群破碎概率的定义。类淑河［11］提出以随机点过程的理论模型刻画风浪破碎的间歇性和随机性，在这一理论框架下，破碎波群发生率正对应点过程的平均强度，概率意义更清晰。

无论是破碎波群发生率还是波群破碎概率，都只是平均意义下的统计量，要完整刻画破碎发生的间歇性，破碎波群间隔及其统计分布才是更合适的研究对象。根据更新过程的理论，只要观测时间足够长，平均破碎间隔的倒数渐近于破碎波群发生率。从而它也可以通过破碎波群间隔估计。

这里主要目标是讨论破碎波群间隔的统计分布。目前还没有见到关于破碎波群间隔的深入研究。而关于波群间隔的研究，则可以追溯到Rice在半个世纪以前的工作。Rice［12-13］讨论作为Gaussian过程的噪声中跨零点之间和噪声流最大值之间的间隔分布;Longuet-Higgins［14-15］分别研究了窄谱的Gaussian过程和平稳随机函数的任意跨任意水平点之间的间隔分布。后来，Ochi and Sahinoglou［2-3］分别讨论了随机海浪的波群持续时间与波群间隔的概率分布，得出的分布更接近于Gamma分布，而不是一般认为的指数分布，提到用更新过程理论计算波群发生概率;Dawson，Kriebel and Wallendorf［4］在实验室设计了一系列海浪实验，验证关于波群特征量的理论结果与实验结果的一致性。

基于一系列风浪破碎实验，研究破碎波群间隔的统计分布。介绍实验和破碎波群间隔的定义;给出了实际破碎波群间隔序列的直方图及其分布拟合，并利用Kolmogorov-Smirnov检验对间隔序列进行了分布拟合检验，讨论了破碎波群发生率与平均破碎波群间隔的关系。

1 实验及破碎波群间隔的定义

1.1 实验

实验在大型风浪流水槽中进行。实验水槽尺寸65.0 m×1.2 m×1.5 m(长×宽×高)，实验时水深0.70 m。波面位移采用实验室自主研发的OUC-2型通道钽丝测波仪测量，采样频率为25 Hz。实验风区选择离出风口 30.0 m 和 34.2 m 两个位置，在每一位置，设计 6.35 m/s、7.0 m/s、7.5 m/s、8.0 m/s和 9.0 m/s等不同风速，共进行了30次风浪破碎实验。实验时实验者借助连接于测波仪的电容器标记通过观测点的破碎事件，破碎标记信号与波面信号同步。现场有一台Sony录像机对着观测点波面连续录像，以备事后校核破碎标记。

1.2 破碎波群间隔的定义

根据Ochi and Sahinoglo［2-3］中提到的波群定义方法，对波峰点利用三次样条插值获得包络，超过某一阈值水平的包络中所包含的一组相邻的波称为一个波群，如图1所示，其中PQ两点之间包含的4个波，可视为波群;而MN两点间只包含一个波峰，因此不能称为波群。在此之前先利用RWR(riding wave removal method)方法滤掉了原始波面信号中的畸行波。包含现场破碎标记信号的波群称为破碎波群，这种方法的判定结果与采用其它破碎判据方法判定的破碎波群有很好的一致性。破碎波群间隔定义为两个相邻破碎波群中第一个破碎标记之间的时间间隔。

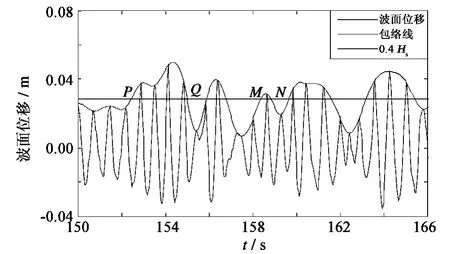
图1 波群的定义Fig.1 Definition of intervals between breaking wave groups

关于波群的阈值水平，Dawson，Kriebel and Wallendorf［4］曾使用过0.2～0.6倍的有效波高。通过分析发现，如果阈值水平过低，波群内包含非接连破碎波的波群数目就增多;反之，如果阈值水平过高，包含破碎波的波群数目就过少。经反复比较，选定波群阈值水平为0.4倍的有效波高。

2 结果与分析

2.1 破碎波群间隔的分布拟合检验

为便于比较不同海浪状态下破碎波群间隔的统计分布，先将破碎波群间隔无因次化，即将每个破碎波群间隔(TBG)除以相应波面信号的谱峰频率对应的周期(Tp)。图2显示了四个实验信号无因次破碎波群间隔序列的直方图及拟合曲线，实线和虚线分别代表拟合的指数分布和Gamma分布的密度函数曲线。指数分布在大部分情形下能较好的拟合实际分布，但有些情形则偏离较大;而Gamma分布似乎能拟合所有情形的实际分布。众所周知，指数分布是Gamma分布的一种特殊情形，Gamma分布可视为指数分布的一种推广。

图2 无因次破碎波群间隔的实际分布与拟合分布Fig.2 Densities of dimensionless intervals between breaking wave groups and their fitted distributions

更严格的结论需要借助分布拟合检验给出。Kolmogorov-Smirnov检验(以下简称K-S检验)是一种有效的分布拟合检验方法。借助Matlab提供的kstest函数，对每个实验信号的破碎波群间隔序列分别进行了指数分布和Gamma分布的K-S检验。图3(a)、(b)分别给出了30个实验信号破碎间隔序列的指数分布拟合检验和Gamma分布拟合检验的结果。每个星号代表一个检验的P-value值，如果P-value值小于给定的显著性水平α，则拒绝原假设，否则不拒绝，图中水平线都表示α=0.05显著性水平。不同信号的检验结果按照风速大小自左向右排列，相同风速的纵向排列。图3(a)中除了3个信号的P-value值小于0.05外，其余27个信号都大于0.05，意味着只有3个信号拒绝了破碎波群间隔服从指数分布的原假设。图3(b)中所有P-value值均在0.05显著性水平之上，即对所有信号都不能拒绝破碎波群间隔服从Gamma分布的假设。

2.2 平均破碎波群间隔与破碎波群率的关系

如前所述，波群破碎率(bgb)为单位时间内破碎波群发生的个数，即bgb=ngroup/T，其中ngroup为一段长度为T的时间段上发生破碎的波群数。从图4中可以看出:破碎波群发生率与平均破碎波群间隔Tmean近乎呈倒数关系。

2.3 相同实验条件下破碎间隔的同分布检验

K-S检验不仅可以检验单样本是否服从某种指定分布，还可以检验两样本是否来自同一分布。由此猜测，相同实验条件下不同信号的破碎波群间隔序列应该是同分布的。为此，对它们进行了两两的K-S同分布检验，同风区、同风速下的实验信号共61对，其中只有3对K-S检验的P-value值小于0.05，其余58对都大于0.05。这意味着，在大多数情形下，不能拒绝相同实验条件下的破碎波群间隔同分布的假设。图5显示的即为在相同实验条件下两两信号对应的破碎波群间隔序列的同分布检验的P-value值。

图3 指数分布和Gamma分布K-S检验的P-value值Fig.3 The P-values of the K-S tests on exponential distribution and Gamma distribution

图4 波群破碎率与平均破碎波群间隔关系Fig.4 The correlation of group breaking rate and average time intervals between breaking groups

图5 同风区同风速下的同分布检验的P-value值Fig.5 The P-values of the K-S tests on the same distribution

3 结语

基于一系列实验室风浪破碎实验，讨论了破碎波群间隔的统计分布。数据分析结果表明所有实验信号的破碎波群间隔都服从Gamma分布，相同实验条件下的破碎波群间隔服从相同的分布。这意味着破碎波群的发生过程极可能是一种更新过程。而低风速情形的大部分破碎波群间隔服从指数分布，这时的更新过程简化为齐次Possion过程，一段时间内发生破碎的波群数服从Poisson分布，从而单位时间内破碎波群发生的个数，即波群破碎率，与平均破碎波群间隔呈倒数关系，实验结果也验证了这一点。

Ochi and Sahinoglo曾提到波群的出现可视为一更新过程，而波群以一定的概率发生破碎，因而破碎波群形成的过程即可以看作是波群过程的一种随机稀疏。从这个角度看，本结果是自然的。

也讨论过波群阈值水平取0.5倍的有效波高的情形，尝试过其它判据判别破碎的结果，所得结论与上述结论类似，不再赘述。

有两方面需要说明一下，一是讨论的间隔，仅是破碎波群的间隔。实际观测中，还经常有不在波群中的破碎，破碎波群的发生又可以看作是破碎过程的一种随机稀疏，将另文讨论实际破碎间隔的分布。二是K-S检验要求所拟合的分布参数已知，这里使用的检验中，指数分布和Gamma分布的参数都是借助样本利用极大似然估计获得，这样结果可能更倾向于接受原假设。

［1］Longuet-Higgins M S.Stochastic properties of wave groups in a random sea state［J］.Philos.Trans.Roy.Sco.，London，1984，312(A):219-250.

［2］Ochi M K，Iorandnis I Sahinoglou.Stochastic characteristics of wave groups in random seas，Part1:Time duration of and number of waves in a wave group［J］.Applied Ocean Research，1989，11(1):39-50.

［3］Ochi M K，Iorandnis I Sahinoglou.Stochastic characteristics of wave groups in random seas，Part2:Frequency of occurrence of wave groups［J］.Applied Ocean Research，1989，11(2):89-99.

［4］Dawson，Kriebel，Wallendorf.Experimental study of wave groups in deep-water random waves［J］.Applied Ocean Research，1991，13(3):116-131.

［5］Donelan M，Longuet-Higgins M S，Turner J S.Periodicity in whitecaps［J］.Nature，1972，239:449-451.

［6］Holthuijsen L H，Herbers T H C.Statistics of breaking waves observed as whitecaps in the open sea［J］.J.Phys.0ceanogr.，1986，16:290-297.

［7］Ochi M K，Tasi Cheng-Han.Prediction of occurrence of breaking waves in deep water［J］.J.Phys.Oceanogr.，1983，13:2008-2019.

［8］Ding Li，Farmer D M.Observations of breaking surface wave statistics［J］.J.Phys.Oceanogr.，1993，24:1368-1387.

［9］Banner M L，Babanin A V，Yong I R.Breaking probability for dominant waves on the sea surface［J］.J.Phys.Oceanogr.，2000，30:3145-3160.

［10］Babanin A V.Breaking of ocean surface waves［J］.Acta Physica Slovaca，2009，59(4):305-535.

［11］类淑河.风浪破碎的随机性、非线性和能量耗散特征研究［D］.青岛:中国海洋大学，2010.

［12］Rice S O.The mathematical analysis of random noise［J］.Bell System Tech.Journal，1945，24:46-156.

［13］Rice S O.Distribution of the duration of random noise［J］.Bell System Tech.Journal，1958，37:581-635.

［14］Longuet-Higgins M S.The statistical analysis of a random moving surface［J］.Philos.Trans.Roy.Sco.，London，Ser A，1957，249:321-387.

［15］Longuet-Higgins M S.The distribution of intervals between a stationary random function［J］.Philos.Trans.Roy.Sco.，London，Ser A，1962，254:389-404.

Statistical distribution for time intervals between breaking wave groups

TIAN Wen-jing1，LEI Shu-he1，GUAN Chang-long2，MA Hai-yan1，XUE Chuan1
(1.Department of Mathematics，Ocean University of China，Qingdao 266100，China;2.Physical Oceanography Laboratory，Ocean University of China，Qingdao 266100，China)

Based on a series of laboratory experiments on wind wave breaking，the distribution of time intervals between successive breaking wave groups is discussed.The wind speeds are different between 6 and 9 m/s.Here，breaking intervals are defined as the time intervals between the moment of the first breaker in the two successive breaking groups.Breaking waves are identified by wave surface displacement and breaking marks record.Kolmogorov-Smirnov test is applied for distribution fitting test.The results from a series of hypothesis tests suggest that:1)it is accepted that the distribution of time intervals between successive breaking wave groups is Gamma distribution，which is true for all the experiments;and 2)under low wind speed，it would be exponential distribution，a special case of Gamma distribution;3)distributions for time intervals between successive breaking wave groups under the same experimental conditions are identical.These results imply that the wind wave breaking observed at a fixed position can be viewed as a renewal process.

wind wave breaking;wave group;time intervals between breaking wave groups;Gamma distribution;renewal process

P731.2

A

1005-9865(2012)04-0149-05

2011-10-19

国家自然科学基金重点资助项目(40830959)

田文婧(1986－)，女，山东莒县人，硕士生，主要从事应用概率统计的研究。E-mail:tian2008fly@163.com