斜坡上封闭式水平板波浪上托力分布试验研究

王端宏，周益人

(1.南京水利科学研究院勘测设计院，江苏南京 210029;2.南京水利科学研究院 河流海岸研究所，江苏南京 210024)

斜坡上封闭式水平板波浪上托力分布试验研究

王端宏1，周益人2

(1.南京水利科学研究院勘测设计院，江苏南京 210029;2.南京水利科学研究院 河流海岸研究所，江苏南京 210024)

通过系列模型试验，对斜坡上尾部封闭式平板结构波浪上托力沿板宽分布进行了详细分析，提出板下最大冲击压强和最大总上托力并不一定同时出现，其分布形态可分为局部冲击型和均匀型。由于封闭空气层和底部斜坡影响，较大总上托力形成机理不尽一致，其均匀分布宽度也不相同，可分为气压型和反射型两类，由此提出分类标准，并分别得到压强分布的计算公式。

斜坡上平板;波浪;上托力分布

在对接岸码头面板结构进行设计时，不仅需要知道波浪产生的最大冲击压强或总上托力，还需要了解对应的压强沿板宽分布。各国学者为此做了相当多的理论和试验研究，并提出各自波浪上托力和相应的压强分布经验公式。由于影响波浪上托力的因素非常复杂，而试验条件和数据通常又存在着一定的局限性和离散性，由此得到的各种上托力经验关系本身就存在较大的差别，因此，在确定其相应的压强分布关系时，通常根据自己的试验资料将其假定为某种分布，而缺乏必要的论证和说明。

对于波浪作用下板上发生最大冲击压强或最大上托力时的压强分布，以往的研究成果相对比较简单，概括起来大致分成两种观点:一种认为板上的压强按波面形状分布［1］，见图1，板上各点压强p可由下式得到:

式中:p为波浪上托力压强(kN/m2);β为压力反应系数，当上部结构的宽度约在10 m以下时，可取β=1.5，当上部结构的宽度较大时，可取β=2.0;Δh为超高(m);η为波峰面在静水面上的高度(m)，由二阶Stocks波理论算得:

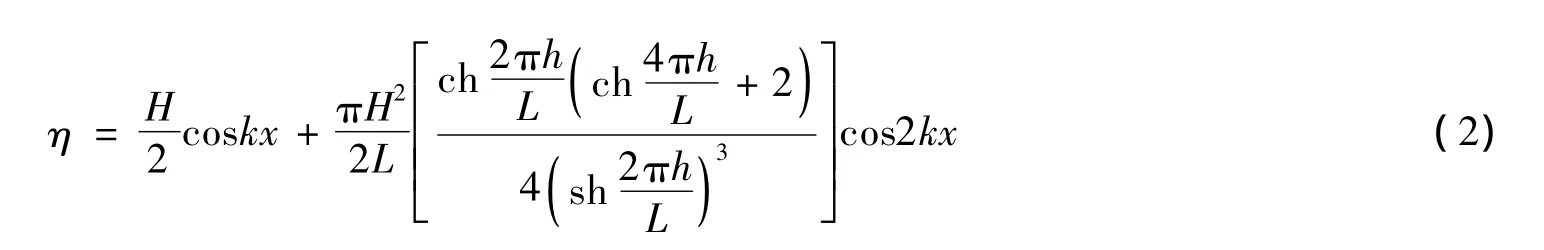
另一种认为平板发生最大冲击压强或上托力时，板上压强在一定宽度内均匀分布(合田良实［2］，过达［3］等)，见图2。但不同的研究者所取的分布宽度l也不尽相同，合田良实［2］取压强的计算宽度l=L/4，而过达等［3］认为l应取为L/8～ L/9，其中L为波长。

由此可见，由于各研究者所依据的试验结果可能具有一定的局限性，给出的压强分布结果之间的差别还是相当大的，应对各种波况及边界条件下，发生最大冲击压强和总上托力时的压强分布进行详细的分析。通过系列模型试验，对斜坡上尾部封闭水平板波浪上托力压强分布进行研究，并在此基础上给出一个比较合理的压强分布计算公式。

图1 波面型上托力分布Fig.1 Waveform pattern of distribution of uplift pressure

图2 均匀型上托力分布Fig.2 Uniform pattern of distribution of uplift pressure

1 上托力试验概况

1.1 试验设备和方法

本次试验在波浪水槽内进行，水槽尺寸为180 cm×180 cm×6 200 cm(宽×高×长)。水槽工作段在纵向预先被分隔成两个部分，其宽度分别为60 cm和120 cm，试验段设在60 cm宽部分，另一部分用以扩散造波板二次反射波能。水槽两端均铺设消浪缓坡，以减少波浪的反射。波浪水槽一端安装有从丹麦引进的推板式造波机，由计算机系统控制，可产生试验所需的波浪。

试验段的中部预先用水泥做好斜坡，坡度分别为1∶2和1∶3两种。在斜坡上方放置一块聚氯乙烯试验平板，尾部封闭，平板宽度与水槽试验段宽度相等，为60 cm，厚1 cm，长度分别为100 cm和50 cm两种。试验平板底部安装有传感器探头，在平板两侧布置成两排，每排沿平板纵向等间距排列，间距为5 cm，对上述两种不同长度的试验板，每排传感器个数分别为20只和10只。由于波浪发生冲击时的上托力很大，试验平板由专门设计的支架水平固定在水槽的不同位置，其高程可按试验要求随意调节，见图3。

采用规则波进行上托力系列试验。考虑到平板、斜坡和波浪的影响，平板的宽度B分别取50 cm和100 cm，坡比m分别为2和3，坡脚水深70 cm，入射波高为5～30 cm，周期1.0～3.0 s，平板底面与静水面之间的距离为-2～8 cm，每组试验变化幅度为2 cm。对上述条件进行组合，试验组次约150组。

图3 波浪水槽布置示意Fig.3 Layout of wave flume

试验采用间歇式生波方式，以消除波浪的多次反射，生波时间约为30～45 s，待水面平静后再继续造波试验。每一组次试验重复进行3次，以确定试验数据的可靠性。

1.2 试验数据采集

以往的研究表明，波浪在对平板作用时，平板下的压强主要由两部分组成:一个是瞬时快速上升的冲击压强，另一个是缓慢变化压强。其中，冲击压强通常远大于缓变压强，变化也更为复杂，为研究平板上托力的重点。由于冲击压强作用的时间非常短，不同的采样频率所得结果差别较大，这就要求上托力测量有较小的采样间隔，以准确反映冲击压力的瞬时量值。在平板波浪上托力预备试验中，当采样时间间隔小于1/125 s时，压强值的变化不大，因此，本次试验选用的采样时间间隔为1/125 s。

2 试验结果和分析

2.1 平板底部波浪压强特征

影响码头面板上托力压强分布的因素很多，其变化也非常复杂。与透空式平板波浪上托力变化过程一样［4］，即使对于同样的波浪要素和边界条件，斜坡上封闭式水平板每一周期内不同时刻面板底部上托力分布也随时间而变化。由于上托力较小时对面板的破坏影响较小，这里将重点讨论上托力较大时的压强分布。图4为不同波浪和边界条件下压强随时间的变化过程。

图4 平板下压强随时间变化过程Fig.4 Pressure characteristics on horizontal plate observed in wave flume experiment

与以往的试验结果类似，上托力压强随时间周期性变化，主要表现为一个瞬时冲击部分和一个缓慢变化部分，前者称之为冲击压强，后者与波面上升高度和超高Δh有关。试验结果表明，斜坡上封闭式平板的冲击压强大致可分为两种类型:一种是在缓变压强变化过程中，有一个迅速上升的瞬时冲击压强，称为单峰型，但这种单峰型远比透空式情况复杂，当波浪周期较小时，类似于透空式平板，瞬时冲击压强后紧随着一个缓变压强，而当波浪周期较大时，这个冲击压却出现在一个周期的中后部，见图4(a);另一种开始时是一个瞬时冲击压强，但在紧随着的缓变压强变化过程中，又出现一个或多个迅速上升的冲击压强，也就是说在一个周期内出现两次或多次冲击，称为双峰型或多峰型，这种冲击类型大多出现在平板的尾部，在板宽较小时，也会出现在板前，见图4(b)。试验结果表明，波浪冲击压强类型不仅与波浪条件和平板上的位置有关，而且即使在同样位置和波浪条件下，有时也会随时间的变化而变化。

图5为同一种波浪条件下，平板不同位置测点的压强随时间变化。由图可见，冲击压强的大小在各测点并不相同，也没有明显的变化规律，其发生冲击的时间也不相同，也就是说，同一时刻板上各点并不同时发生最大冲击压强。但与透空式平板不同的是，其发生冲击的时间似乎并不随x(距板前缘的距离)的增大而后移，这表明:波浪接触斜坡上平板后，由于板后波浪的出路已经堵死，最大冲击压只是随时间改变，而不能继续向前推进。而当板宽较长时，在板后会出现一个新的冲击点(图5(b))，在板后最大，甚至超过波浪开始接触平板时的第一次冲击压强(图5(d))，从其发生的时间来看，这个第二冲击压强应该是由平板后部向前传播的。

2.2 平板底部波浪压强分布

图6为不同时刻平板下出现较大冲击压强时波浪压强分布;图7为不同超高条件下一个周期内不同时刻平板下出现较大总上托力时波浪压强分布的变化，图中压强分布编号间隔为1/125 s。

图5 同时刻板下各测点压强变化Fig.5 Pressure histories in different locations under horizontal plate

由图可见，与透空式平板类似［5］，当平板底部局部发生最大冲击压强时，平板最大总上托力并不一定同步出现，它们所对应的压强分布形式分别为局部冲击型和均匀型。但对应较大总上托力时的均匀型压强分布由于受到板下封闭空气层和斜坡的影响，远较透空平板复杂。当波陡(H/L)较大而相对超高(Δh/H)较小时，发生最大上托力时的压强分布通常均匀分布在整个板宽范围(图7(a))，即使在相对板宽(B/L)很大(B/L=0.65)时，上托力仍然沿整个板宽均匀分布，此时，分布宽度l一般等于平板宽度B，入射波波长(或波浪作用平板的宽度x)与分布宽度的关系看上去远不如透空式情况密切;而当波陡(H/L)较小且相对超高(Δh/H)较大时，上托力的分布变得相当复杂，出现最大总上托力的分布有时沿整个平板的均匀分布，有时表现为很小范围的均布，分布宽度l的变化幅度非常大，并且随着分布宽度l的增大，均布压强值也逐渐减小，由图7(b)可见，这种变化是从板后向板前推进的。

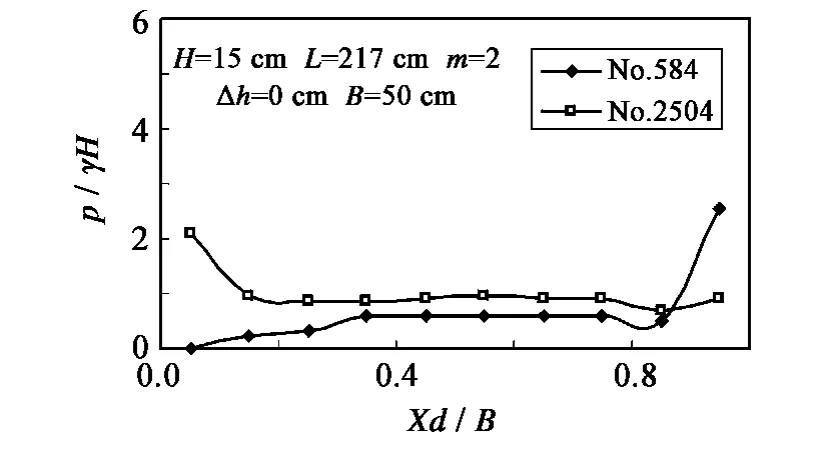
图6 不同时刻板下发生较大冲击压强时波浪压强分布Fig.6 Pressure distributions along horizontal plate corresponding to the maximum impact pressure in different time

图7 一个周期内不同时刻板下发生较大总上托力时压强分布变化Fig.7 Distribution of pressure intensity along the plate width corresponding to the maximum total uplift forces in a period

上述现象虽然非常复杂，但却并非无章可循。由试验资料分析可知，斜坡封闭式平板一个波周期内所受的最大总上托力通常由两种原因产生:一种是在波浪开始冲击平板前部的瞬间产生的，此时由于平板尾部封闭，板下封存的空气无法从板后排出，只能通过板前波面与平板间的缝隙逸出，因此，在板下形成一片遍布整块平板的有压空气层，对平板产生上托力，这种状况下的上托力主要由板下封入的空气引起的，与透空式情况下由波浪传播产生的均布型［5］总上托力形成机理不同，在波浪作用平板的瞬时就可能在平板下不同点产生很大的压强，其分布也更趋均匀，可称为气压型分布;另一种是在波浪冲击平板前部后，传播到岸壁并反射回来，再对平板冲击而产生的，此时，由于斜坡的影响，传播至平板尾部的波浪波高将增大很多，对平板尾部产生很大的冲击压，并沿离岸方向由板后向板前传播，这种上托力分布的变化规律与透空式情况类似，只是传播的方向相反，可称为反射型分布。这两种分布类型可能同时存在于同一种波浪和边界条件，但对应于不同的波浪形态和边界条件，起主导作用的分布类型是不同的。当波陡较大而相对超高较小时，由于波浪很难传播到板后，最大总上托力一般呈现气压型分布;当波陡较小而相对超高较大时，板下封存空气易于从板前逃逸，此时封闭空气层引起的气压型上托力将逐渐减小，但同时，由于相对超高的增大，平板对波浪的影响减小，波浪也更易于传播至平板尾部，受到岸壁的反射作用而形成较大的冲击压力，此时最大总上托力一般对应反射型分布;当波陡和相对超高值处于上两种情况之间时，也可能会发生两种分布的总上托力处于同一量级的现象，即此时发生的最大总上托力可能呈气压型分布，也可能呈反射型分布。

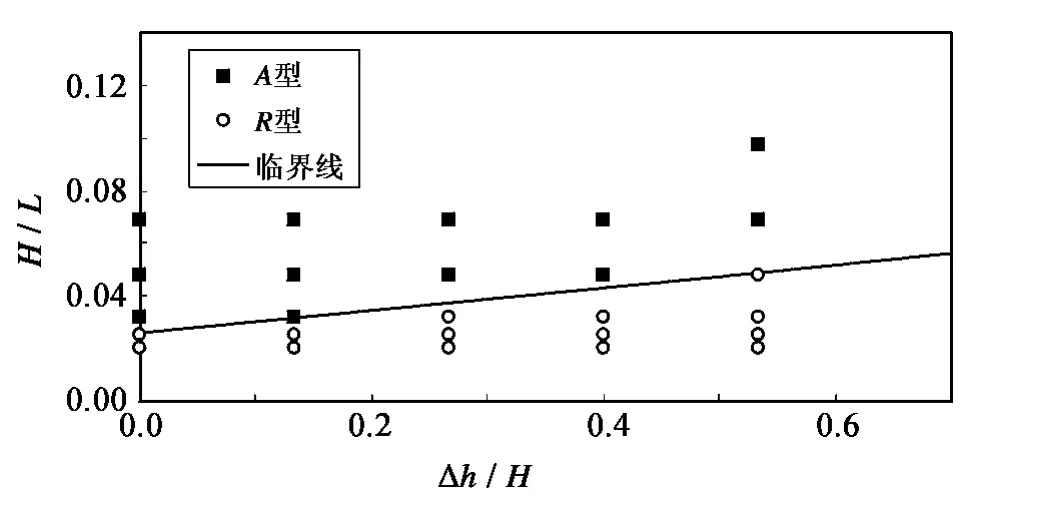
图8 两种分布类型区分标准Fig.8 Classification criterion of distribution patterns

不同波浪和边界条件下的最大总上托力存在不同的分布类型，因此，在对斜坡上封闭水平板波浪上托力分布规律进行研究时，首先必须确定分类标准。由试验数据可知，上托力分布类型与入射波波陡和平板的相对超高有关，并且波陡因子似乎影响更大，由此以波陡为纵坐标，相对超高为横坐标，将不同分布类型的试验资料绘于图8，图中的“A型”表示气压型分布，“R型”表示反射型分布。

由图8可见，两种分布类型可以由一条直线很好地区分开来，直线的上部为气压型，下部为反射型。由此，可得到两种分布类型的分布标准，即

2.3 压强分布计算

由上述压强分布分析结果可知，对于局部冲击型分布，可采用透空式平板［5］结果，分布宽度l0与入射波波长L成正比，即

对于均匀型分布，可分为气压型和反射型。气压型分布比较简单，发生最大总上托力时的压强通常为沿整个板宽的均匀分布，分布宽度l1就等于板宽B，即:

反射型分布的情况要复杂得多。上托力压强虽然仍可按均布荷载处理，但分布宽度l2的变化范围相当大，并且在各种分布宽度下，都可能具有很大的总上托力，因此，在解决该类型的分布规律问题时，首先必须确定分布宽度l2的范围。由试验资料可见，发生该类型冲击时，最大冲击首先从板后开始，并逐渐向板前传播，在一定的传播范围内通常具有较大的冲击压强，并且随着传播距离的延长，冲击压强逐渐减小，而总上托力却随着传播长度的增加，呈现开始不断增大然后再逐渐减小的过程，见图7(b)。在这段范围内，最大总上托力可能出现在不同的传播长度上，虽然其前锋与入射波迭加可能产生较大的局部冲击压强，但总体上看，上托力压强分布在一定范围内还是比较均匀的。因此，出现最大总上托力的最小分布宽度l2min可以由文献［6］给出的最大总上托力和最大冲击压强计算公式确定，即

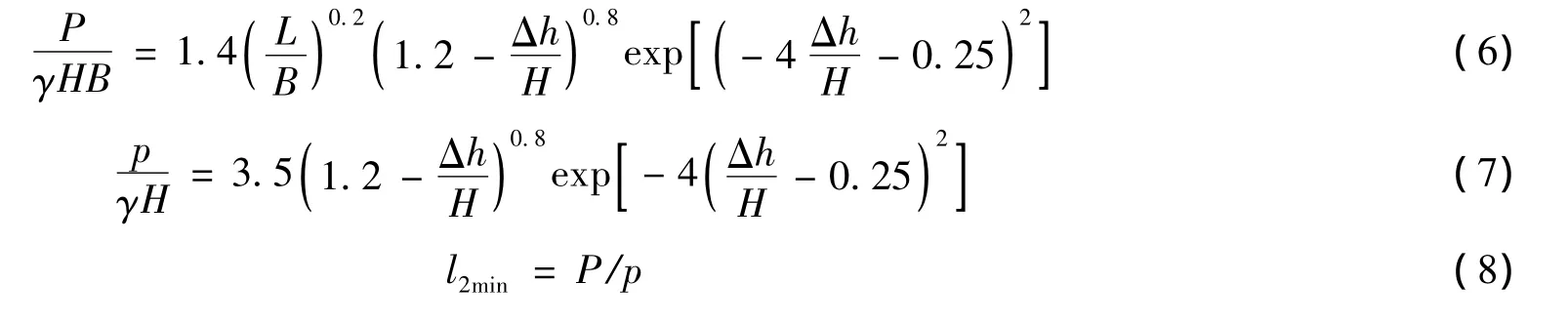
式中:P为单宽最大总上托力计算值，p为板上最大冲击压强计算值。按式(3)给出的分类标准，将斜坡上封闭式平板相应最大总上托力和最大冲击压强计算公式代入，得:

尽管本次试验中大多数情况下反射型最大分布宽度就等于板宽，但由于反射型分布经常出现在相对超高较大时，而波浪作用平板的宽度可能会变得很小，以至于影响到分布宽度的上限，因此，本次研究根据实测资料得到最大分布宽度l2max为:

当l2max的计算值大于板宽B时，取l2max=B。

在对反射型分布荷载进行计算时，分布宽度可以从平板尾部算起，在l2min和l2max范围内取任意值，然后将总上托力的计算值除以所取的l2，即可得到反射型分布的平均压强，可供各种设计要求选择。

按上述计算步骤，可分别得到斜坡封闭式平板气压型和反射型分布。图9和图10分别为两种类型计算与试验实测分布的比较，计算结果基本反映了实际情况。

图9 气压型分布计算值与实测值比较Fig.9 Comparison of calculated distribution with experimental data in A-type

图10 反射型分布计算值与实测值比较Fig.10 Comparison of calculated distribution with experimental data in R-type

3 结语

通过系列试验研究，对斜坡上封闭式平板下波浪上托力压强分布进行了分析，结果表明:板下较大冲击压强和较大波浪总上托力通常不同步出现，其压强分布主要有两种类型，一种为局部冲击型，另一种为均匀型。局部冲击型可按透空式平板处理，而对应于最大总上托力的均匀型分布因受到板下封闭空气层和斜坡的影响，变化非常复杂。当波陡较大而相对超高较小时，压强分布通常均匀分布在整个板宽范围，称为气压型;而当波陡较小且相对超高较大时，上托力的分布有时沿整个平板均布，有时表现为很小范围的均布，分布宽度l的变化幅度非常大，称为反射型。由于在码头面板设计中不仅需要考虑波浪对整个码头面板的最大总上托力，还要考虑单块面板局部冲击压强，因此，应按不同要求，同时进行各种类型的上托力分布计算。为此，这里提出了各种分布类型的计算公式，基本满足了设计要求。

需要提出的是，由于本次试验传感器布置间距为5 cm，而发生最大冲击压的分布宽度又很小，因此，这里提出的平板底部的波浪上托力局部冲击型分布宽度公式只是借助于间接资料的论证，应在今后的工作中进行进一步的研究。

［1］交通部第一航务工程勘测设计院.海港工程设计手册(中)［M］.北京:人民交通出版社，1994:52.

［2］合田良实.構造物に働く波力［R］.1967年度水工学に関する夏期研修会講義集，B.海岸港湾コース，1967.

［3］过 达，蔡保华.透空式建筑物面板波浪上托力计算［J］.华东水利学院学报，1980，(1):14-33.

［4］ZHOU Y R，CHEN G P.Uplift pressure of wave on a horizontal plate［J］.China Ocean Engineering，2003，17(3):355-368.

［5］周益人，陈国平，黄海龙，等.透空式水平板波浪上托力分布［J］.海洋工程，2003，21(4):41-47.

［6］周益人，陈国平.高桩码头面板波浪上托力计算［R］.南京:南京水利科学研究院，2001.

Distribution of uplift pressure of waves along a horizontal plate of wharf on a slope

WANG Duan-hong1，ZHOU Yi-ren2
(1.Design and Consulting Corp.of Nanjing Hydraulic Research Institute，Nanjing 210029，China;2.River and Harbor Dept.of Nanjing Hydraulic Research Institute，Nanjing 210024，China)

This paper presents the result of an experimental study on the distribution of uplift pressure along a horizontal plate of a wharf on a slope exposed to a regular progressive wave.The results show that the distributing patterns corresponding to the maximum uplift pressure and the maximum uplift force respectively are different.Owing to the effects of air cushion closed under the plate and slope under the plate，there are two basic types of distributing patterns of uplift pressure corresponding to the maximum uplift force.A criterion，which may distinguish these two types of distributing patterns，is proposed.Finally，some empirical relationships are obtained for prediction of the two distributing patterns.

horizontal plate on slope;wave;uplift pressure distribution

TV139.2

A

1005-9865(2012)03-0045-06

2011-07-05

王端宏(1965-)，男，江苏南京人，高级工程师，主要从事海岸工程设计和研究工作。E-mail:dhwang@nhri.cn