深孔爆破装药结构优选数值分析方法及其应用

刘优平 ，龚 敏黄刚海

（1. 北京科技大学 土木与环境工程学院，北京 100083；2. 南昌工程学院 土木与建筑工程学院，南昌 330099；

3. 中国科学院武汉岩土力学研究所，武汉 430071）

1 引 言

在地下采矿工程中，当进行深孔爆破侧向崩矿作业时，常由于爆破后冲作用严重、爆破块度不均等现实问题而影响采矿的后续作业。为此，研究合理的装药结构使岩石得以充分破碎、提高爆破效率、降低成本、并有效地控制爆破危害效应，已成为爆破领域的重要研究课题。

目前，指导现场爆破装药结构设计的方式主要有现场爆破试验及室内模型试验，然而这两种方法成本高、时间长且受场地的严格限制。近年来，随着计算机技术的发展，数值方法成为预测爆破效果的重要方法之一，其低成本、高效率且不受场地限制等优点使其得到广泛应用。在国内，LS-DYNA是分析爆炸应力场最常用的工具：郑祥滨等[1]用其对单螺旋空孔直眼拉槽成腔过程进行数值模拟研究，姜鹏飞等[2]用该工具分析了不耦合装药爆破对硬岩应力场的影响，王鹏等[3]采用该软件对多孔同段爆破漏斗形成机制进行数值模拟研究。这些研究成果及其有效应用展示了LS-DYNA 对爆破过程进行模拟的可行性和有效性。

南方某铅锌矿为实现年产18×104吨铅锌金属量达产，决定采用深孔爆破崩矿高效采矿方法。为使该法尽早应用于生产，矿山选一采场作为试验采场，以确定符合矿山岩石性质的最优爆破参数。鉴于此，本文尝试采用ANSYS/LS-DYNA 分析几种炮孔装药结构的爆炸应力场，提取有用信息，结合爆破破岩机制，预测爆破效果，优选炮孔装药方式，以指导现场爆破作业。

2 爆破数值模拟及分析方法

爆破过程涉及的介质主要有炸药、岩石及炮孔内的空气垫层等，在数值模拟中分别建立其本构模型。模拟采用ANSYS/LS-DYNA，该软件为美国ANSYS 公司和LSTC 公司合作开发的显式非线性动力分析通用有限元程序，可以求解各种二维和三维非弹性结构的高速碰撞、爆炸和模压等大变形动力响应[4－5]。采用该软件进行爆炸分析时，一般有Lagrange 和ALE 两种算法，本文采用ALE 算法。

2.1 材料本构模型及其状态方程

2.1.1 炸药燃烧模型

炸药采用MAT_HIGH_EXPLOSIVE_BURN 模型模拟，爆炸过程中其压力和比容关系采用如下JWL 方程来描述：

式中：P 为压力；V 为相对体积；E0为初始比内能；参数A、B、R1、R2、ω 为试验确定的常数。本文所用炸药的参数如表1 所示。

表1 炸药参数 Table 1 Parameters of explosives

2.1.2 岩石材料弹塑性模型

炸药爆炸时近区岩体发生屈服以致破碎，应变很大，应变率效应明显，采用包含应变率的塑性随动模型(MAT_PLASTIC_KINEMATIC)经证明是比较合适的[6]。该模型应变率用Cowper-Symonds 模型来考虑，用与应变率有关的因数表示屈服应力：

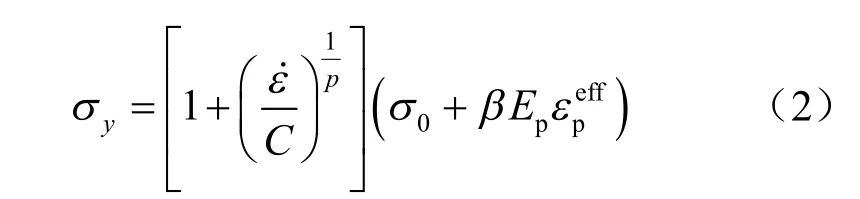
式中：σ0为初始屈服应力；为应变率；C 和p 为Cowper Symonds应变率参数；为有效塑性应变；Ep为塑性硬化模量，由下式给出：

式中：tanE 为切线模量；E 为弹性模量，本文涉及的岩石主要为灰岩和砂页岩，关于两个应变参数C和p 的取值，参考Yang 等[7]所做的在不同应变率下岩体的应力-时程曲线和应力-应变关系的成果，并根据文献[6]研究的结果，两个应变参数取值分别为2.5 s-1和4.0，表2 给出了岩石材料参数。岩石动抗拉强度的取值，由于缺乏度验数据，难以确定其精确值，参考文献[8－9]所取的值（文献[8]取40 MPa，文献[9]取100 MPa），并与本文岩石的大致强度关系对比，本文取岩石动态抗拉强度为90 MPa。

表2 岩石参数 Table 2 Parameters of rock

2.1.3 空气垫层材料模型

本文爆破模拟中炮孔采用不耦合装药结构，用空模型(MAT_NULL)来模拟炮孔内的空气垫层。选用如下线性多项式状态方程：

式中： C0～ C6为常数；μ 为比体积； E0为内能与初始体积之比。计算参数如下表3 所示。

表3 空气垫层参数 Table 3 Parameters of air-dech

2.2 爆破破岩机制

有自由面的爆破过程，炸药爆炸后，首先在炮孔周边形成一定范围的压碎圈；之后冲击波衰减为应力波，其强度不能压碎岩石，但由其产生的径向压缩和径向位移可使岩石出现一定的裂隙区；应力波到达自由面发生反射，以拉伸波的形式往岩石内部传播，当拉伸波强度超过岩石的动态抗拉强度时，岩石发生拉伸破坏。拉伸破坏最先表现为自由面附近岩块的“片落”，并逐渐往爆心传播。

2.3 爆破效果评估方法

爆炸载荷作用下岩石的应力状态非常复杂，在数值计算中寻求一种合理的模型来描述其本构关系尤为重要。在用LS-DYNA 进行爆破仿真过程中，许多研究者[6，9－10]用Von Mises 有效应力来表征岩石的应力特征，分析结果得到了人们的认同和广泛应用。鉴于此，本文采用Von Mises 屈服准则来分析爆破过程中应力场的分布规律及爆破破碎特性。

Von Mises 屈服理论[10]即形状改变比能理论，称第四强度理论。它假设当物体内某点的应力状态对应的畸变能达到某极限数值k 时，该点屈服，即：

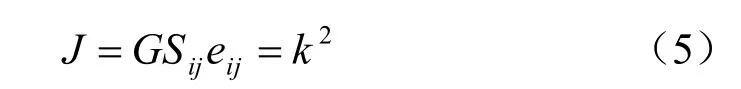
式中： Sij=σij-σmδij； eij= Sij/2G；σij为应力张量；σm为平均应力； δij为Kronecker 符号；G 为材料剪切模量；k 表示材料屈服特征的参数。

在塑性力学中，为了方便使用，将下式定义为有效应力(effective stress)：

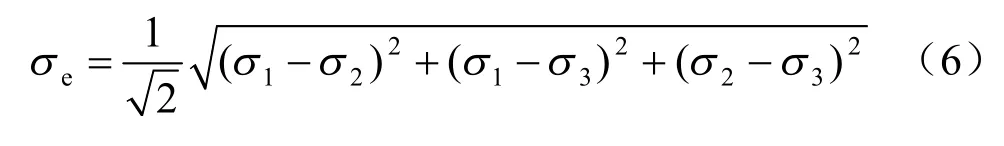
于是，Mises 屈服条件也可以用更为方便的有效应力形式表示，即：

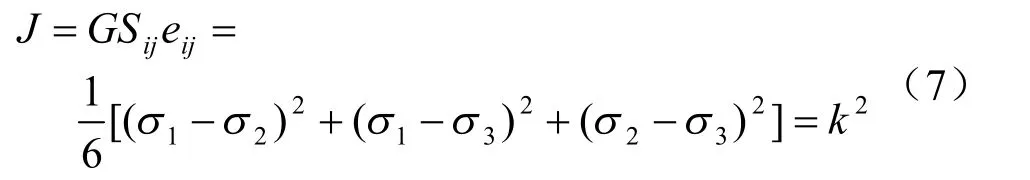
所以，σe==。当k = σt/（以简单拉伸为依据）时，有：

式中：tσ 为抗拉强度。所以，Mises 屈服条件也可表述为，当有效应力达到简单拉伸的屈服极限时，材料进入塑性状态。因此，采用Mises 屈服准则来分析爆破的破碎特性时，可对比处于简单拉伸状态的位置的有效应力与岩石动态抗拉强度来判断该位置是否发生屈服。

从前述爆破破岩机制可以看出：自由面附近发生“片落”是由于岩石所受拉伸应力超过其动抗拉强度引起的。自由面上的单元可认为一直处于接近简单拉伸的状态，因此，用自由面上的单元的Von Mises 有效应力峰值与岩石动抗拉强度进行对比判断该处是否发生屈服是合理的。本文采用以下步骤分析爆炸载荷作用下岩石的破碎特性：

（1）通过数值计算分析，得出炸药爆炸后岩石中一定时间内Mises 有效应力的动态分布。

（2）提取自由面上的关键单元，获取其有效应力时程曲线，读取其峰值并与岩石动抗拉强度进行比较；若峰值大于岩石动态抗拉强度，说明该单元在爆炸载荷作用下发生屈服，可认为该处将发生“片落”现象，否则未发生岩块“片落”。

3 工程应用

3.1 工程概况

图1 显示了南方某地下矿深孔爆破崩矿采矿方法的采矿工艺。采用该采矿方法时，在凿岩硐室打竖直钻孔穿过整个矿体（孔径φ=110 mm，每个采场布置4 排炮孔，排间距为1.867 m，列间距2.2 m）；用掏槽爆破在采场端部形成自由面和补偿空间，根据碎胀系数，余下矿石采用2～4 次侧向爆破进行崩落，采用铲运机（视安全情况偶尔采用遥控铲运机）在出矿硐室进行出矿作业。

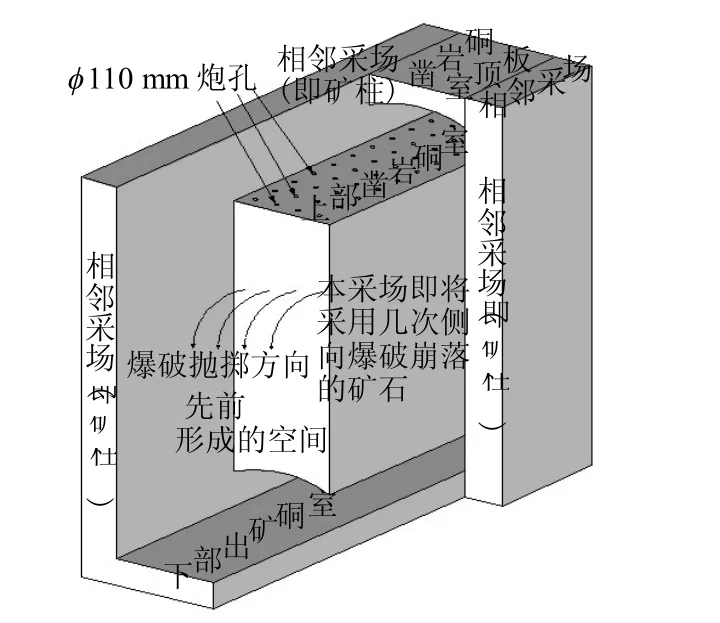
图1 采矿工艺示意图 Fig.1 Mining process schematic diagram

上述采矿工艺具有安全高效、机械化程度高、采切比小等优点。然而，该方法在侧向爆破过程中极易出现问题，如图2 所示。由于前一次爆破最后一列炮孔装药不合理，增强了爆破后冲作用，使前、后两次爆破作业交界处（下称该处为爆破切口）的岩体裂隙扩展甚至贯通，导致临爆区滑下大块矿石，该矿石未经爆破破碎便混入矿堆之中，成为“超级大块”，对出矿作业产生极大影响；同时可造成下次爆破第一列炮孔堵塞、坍塌甚至报废，增大爆破最小抵抗线，很难控制爆破效果。

图2 侧向爆破现场问题说明图 Fig.2 Illustration of problem during lateral blasting

上述问题的出现，使每次爆破最后一列炮孔的装药结构倍受重视，如何优化该列炮孔的装药结构，使爆破获得合适破碎效果的同时确保爆破切口的平整，是爆破设计及现场施工必需解决的问题。

3.2 炮孔装药结构设计

结合矿山实际情况，对炮孔设计了可能采用的6 种装药结构，如图3 所示。这里选用轴向空气间隔装药结构，意在利用空气垫层缓冲爆炸作用力。

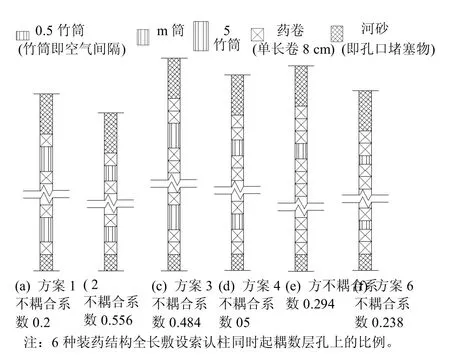
图3 六种炮孔装药结构方案图 Fig.3 Drawing of six kinds of hole’s charging structure

3.3 爆破数值模拟及其结果分析

3.3.1 建模

用ANSYS/LS-DYNA分别对设计的6种装药结构进行爆破模拟，考虑模型的对称性，对计算模型进行简化，对人工边界设置无反射边界条件。最终确定的计算模型宽为4 m，高为10 m；由于模型前、后对称，可取“薄板”型计算模型，模型前、后边界均设置无反射边界条件，避免人为边界对计算产生影响。图4 为数值计算模型，共包含42 640 个单元。

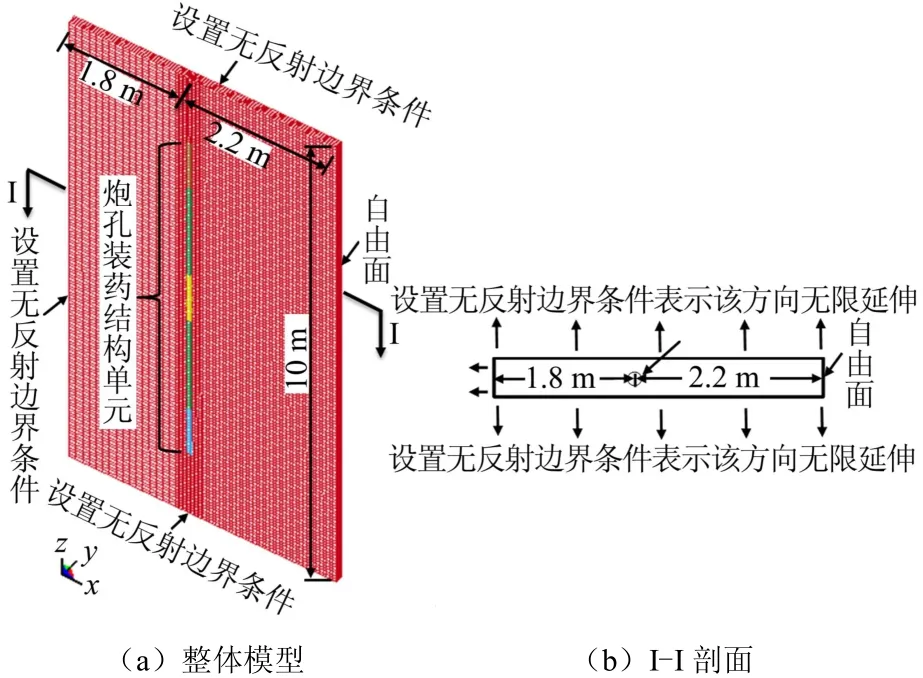
图4 数值计算模型 Fig.4 Model of numerical computation

3.3.2 有效应力场分析

图5 显示了方案1 爆破过程不同时刻的有效应力云图（其他方案应力场限于篇幅不一一列出）。

从图5 可看出，各段药柱同时起爆，t =0.36 ms时，各药柱的应力波开始叠加，t =0.8 ms 时，应力波到达自由面并发生反射（见图中椭圆圈出的部分）；t =3.22 ms 后应力波强度较弱。可见所定爆破模拟时长包含了爆破的整个过程，不会造成数据缺失。

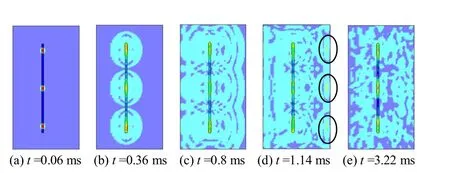
图5 方案1 爆破过程有效应力云图 Fig.5 Effective stress nephogram of scheme 1’s blasting

3.3.3 自由面上单元有效应力分析

提取各7 方案爆破过程中自由面上一系列单元的有效应力时程曲线，并读取其峰值。为使结果具有可比性，每种方案均提取12 个具有代表性的单元（从下至上将单元编号为1#～12#），相邻单元之间的距离均为0.5 m，方案不同、而编号相同的单元在模型中的位置一致。为便于分析，将所获取的数据用曲线形式表示，如图6 所示。

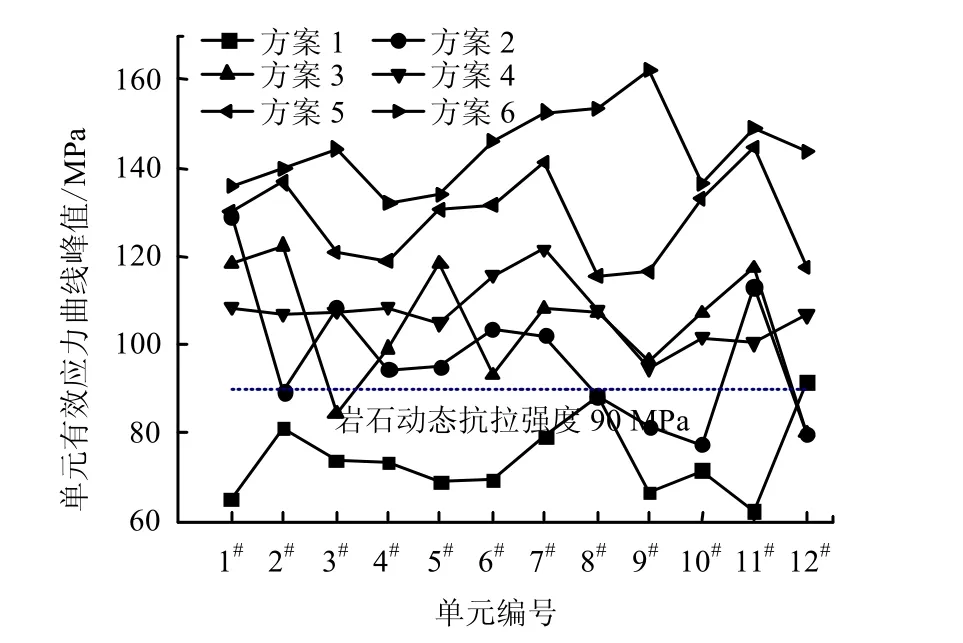
图6 6 种方案的有效应力峰值曲线 Fig.6 Peak value curves of effective stress of six schemes

分析图6 可得：

（1）6 条曲线总体上逐条升高，说明6 种装药方案的爆炸威力逐渐增大，这是由于6 种装药结构的装药量逐渐增大所致。3、4 两种方案的曲线较为接近，说明这两种方案爆炸威力差别不太明显，这是因为这两种方案的装药结构差别较小所致。

（2）从曲线的波动情况上看，2、3 方案波动最大，1、4 方案的曲线相对平缓，其中方案4 的曲线平缓程度最好。曲线的平缓程度反映了爆炸能量分布的均匀程度，故可认为方案4 装药结构的爆炸能量分布得最为均匀，最有利于爆炸能量的充分利用。

（3）单元有效应力峰值低于岩石动抗拉强度则说明该单元未发生屈服，该处未发生“片落”现象。由于所选单元之间相距均为0.5 m，若有一个单元 未发生屈服，则可认为该爆破过程产生大于1.0 m的大块的可能性很大，根据矿山出矿设备参数，应改进爆破方案。观察图6 的6 条曲线，方案1 几乎所有单元均未发生屈服，方案2、3 分别有5 个和2个单元的有效应力峰值未达到90 MPa，余下3 个方案所有单元均发生屈服。由此可认为方案1、2、3装药量不足，不能采用；方案5、6 所有单元的有效应力峰值均远高于岩石动抗拉强度，有可能造成爆炸能量过剩。

据分析，临爆区大块岩体滑落、炮孔坍塌的主要原因是前一次爆破最后一列炮孔装药量过大，过剩的能量大大增加了爆破的后冲作用。因此，应尽量控制炮孔装药量，确定一种恰可爆破劈裂岩石并可得到合适破碎块度的装药方式是解决问题的关键。根据以上3 个分析认识，可确定方案4 是最佳的炮孔装药结构。

3.4 工程应用效果

将本文研究结果应用于矿山试验采场的爆破作业取得了较好效果。图7 为爆破效果照片。

图7 爆破效果照片 Fig.7 Photos of blasting result

从图可以看出，采用设计的第4 种炮孔装药结构获得了平整的爆破切口，未造成下次爆破炮孔的坍塌，爆破切口处可看到残留的炮孔壁，说明所用的炮孔装药结构较好地缓冲了炸药爆炸对炮孔壁的冲击力。从块度照片中可以看出，爆破块度较适中，现场出矿作业过程也未发现大块。由此说明，本文研究结果的工程应用效果较好，基本上解决了矿山深孔侧向爆破存在的问题。

4 结 论

（1）利用深孔爆破仿真过程中的Von Mises 有效应力信息，结合爆破破岩机制及Mises 屈服理论，提出了爆破过程中自由面附近岩石是否发生“片落”的判定方法。

（2）采用ANSYS/LS-DYNA 有限元分析软件，对设计的6 种炮孔装药结构进行了数值模拟，得出了各种装药结构爆破后关键单元的有效应力峰值曲线，应用上述提出的数值分析方法确定了理论的最优方案。

（3）将确定的最优方案应用于实际工程爆破，得到较好爆破效果，基本解决了矿山深孔侧向爆破过程存在的问题，表明所探讨的方法能有效指导爆破设计，可为类似条件下的爆破参数优化及现场问题的解决提供理论依据和技术支持。

[1] 郑祥滨， 璩世杰， 范利华， 等. 单螺旋空孔直眼掏槽成腔过程数值模拟研究[J]. 岩土力学， 2008， 29(9)： 2589－2594. ZHENG Xiang-bin， QU Shi-jie， FAN Li-hua， et al. Numerical simulation of cavity formation process by single helix parallel hole cut blasting[J]. Rock and Soil Mechanics， 2008， 29(9)： 2589－2594.

[2] 姜鹏飞， 唐德高， 龙源. 不耦合装药爆破对硬岩应力场影响的数值分析[J]. 岩土力学， 2009， 30(1)： 275－279. JIANG Peng-fei， TANG De-gao， LONG Yuan. Numerical analysis of influence of uncouple explosive-charge structure on stress field in hard rock[J]. Rock and Soil Mechanics， 2009， 30(1)： 275－279.

[3] 王鹏， 周传波， 耿雪峰， 等. 多孔同段爆破漏斗形成机理的数值模拟研究[J]. 岩土力学， 2010， 31(3)： 993－997. WANG Peng， ZHOU Chuan-bo， GENG Xue-feng， et al. Numerical simulation of formation mechanism of multi hole and same delay time of blasting crater[J]. Rock and Soil Mechanics， 2010， 31(3)： 993－997.

[4] Ansys. Inc.. ANSYS/LS-DYNA user guide[R]. [S. l.]： [s. n.]， 1999.

[5] 时党勇， 李裕春， 张盛民. 基于ANSYS/LS-DYNA8.1进行显式动力分析[M]. 北京： 清华大学出版社， 2005.

[6] 夏祥. 爆炸荷载作用下岩体损伤特征及安全阀值研 究[D]. 武汉： 中国科学院研究生院， 2006.

[7] YANG R， BAWDEN W F， KATSABANIS P D. A new constitutive model for blast damage[J]. International Journal of Rock Mechanics and Mining Sciences， 1996， (33)： 245－254.

[8] 刘智权. 大间距无底柱分段崩落法回采爆破参数的研究[D]. 武汉： 武汉科技大学， 2005.

[9] 刘美山. 特高陡边坡开挖爆破技术及其对边坡稳定性的影响[D]. 北京： 中国科学技术大学， 2007.

[10] 周传波. 深孔爆破一次成井模拟优化与应用研究[D]. 武汉： 中国地质大学， 2004.