考虑基坑开挖影响的群桩基础竖向 承载性状数值分析

王成华，刘庆晨

（天津大学 建筑工程学院，天津 300072）

1 引 言

随着我国城乡建设的发展，桩基础作为大型建筑物、构筑物中运用最多的一种深基础形式，得到越来越广泛的应用。桩基技术的广泛应用，推动了桩基理论研究的不断深入，而桩筏基础作为桩基础主要应用型式，一直是国内外研究的重点和热点。

高层建筑的基础为了满足建筑功能和稳定性的要求，一般要求具有较大的埋置深度，这意味着必须开挖较深的基坑。基坑开挖卸载引起坑底土体产生向上为主的位移，同时也使基坑挡土墙及其外侧土体在两侧压力差的作用下产生水平向位移和因此而产生的墙外土体的位移。在这一过程中基坑内工程桩主要受到两方面影响[1]：一是竖向作用，基坑开挖后，坑内土体应力释放、回弹，带动桩上移，桩身上部承受向上的正摩阻力作用，承受上拔荷载，桩被抬升；桩身下部阻止桩的上移，对桩产生向下的负摩阻力，导致桩在正、负摩阻力的作用下承受拉伸轴力，尤其在软土地区，严重时发生断桩；二是水平作用，当开挖深度较大时，基坑外侧土体的水平位移，使桩在水平力的作用下弯曲，甚至破坏，尤其是软土地区稍不注意就会发生此类事故。

基坑开挖完成后，上覆土体的移去使得桩周中的土体有效应力减小，桩侧摩阻力减小，导致桩的承载力降低。同时由于回弹的作用，桩周存在的侧摩阻力会影响桩侧摩阻力的发展趋势，影响桩的刚度，从而严重影响上部结构的稳定性和可靠性。上海某基坑开挖深度为13 m，基桩检测资料表明，开挖完成后30%工程桩在钢筋笼底部断裂[2]。广东地区某基坑开挖深度为5 m，高应变检测资料表明，40%的基桩承载力达不到要求[3]。因此，基坑开挖对基桩的影响不容忽视，其定量评价对实际工程具有重要指导意义。

本文利用有限元软件ABAQUS，建立了桩筏基础—地基—基坑开挖三维有限元分析模型，研究基坑开挖对群桩基础竖向承载性状的影响，讨论桩顶反力分布、桩身轴力、桩侧摩阻力以及开挖引起的桩身轴线水平位移及其弯矩的变化规律，并以桩侧摩阻力为例，与不考虑基坑开挖的工况进行对比分析。

2 有限元模型及参数

2.1 计算假定

本文采用有限元软件ABAQUS 进行模拟，在算例中，做了以下假定：

（1）计算区域内土体为均质、连续、各向同性；

（2）承台、地下连续墙、支撑和桩体按照线弹性本构关系计算，土体为弹塑性材料，服从Mohr- Coulomb 屈服准则；

（3）桩-土之间接触面单元的本构关系简化为理想弹塑性模型，并假设接触面发生塑性滑动的临界值为0ω =2 mm；

（4）地下连续墙与周围土体始终紧密接触，即在变形过程中，他们之间不产生相对滑动或脱离；

（5）整个模拟过程中不考虑地下水的影响，按总应力法进行分析。

2.2 计算模型

基坑的几何形状、支护结构和桩筏基础的结构形式、荷载分布等均为对称，故选取1/4 结构作为研究对象进行分析。综合考虑模型尺寸与计算机的计算能力，选取土体尺寸：长为60 m，宽为60 m，高为88 m。

建模分析中土体、桩体、地下连续墙和筏板均用三维8 节点实体单元C3D8R。支撑采用空间桁架单元T3D2。在考虑基坑开挖影响时，为简化分析，假设地下连续墙和周围土体不发生相对滑移，接触面上墙体单元和土体单元共同变形，故采用绑定约束。为了重点研究桩-土相互作用、考虑基桩和土体之间存在的变形不协调和相对滑移，很好地反映桩-土相互作用机制故在桩-土接触面上设置接触单元，采用库仑摩擦模型，摩擦系数取0.35。有限元建模及网络划分如图1、2 所示。图3 给出了承台、桩位与坐标轴相互关系的平面图。

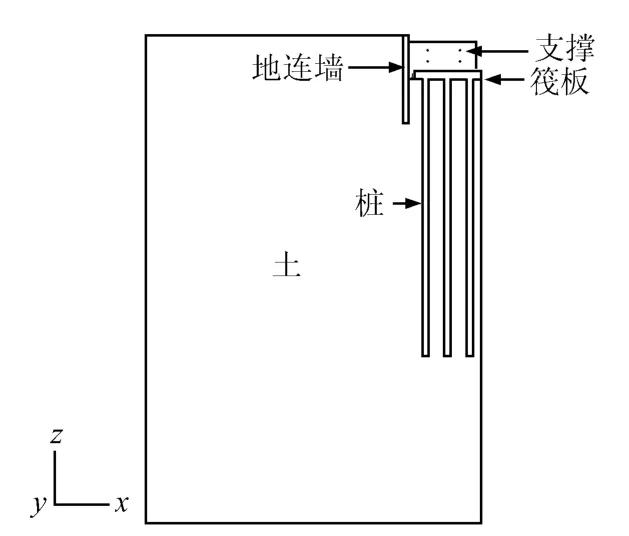
图1 开挖后模型1/4 剖面图 Fig.1 Profile of 1/4 model after excavation

图2 整体模型有限元网格 Fig.2 Finite element meshes of the entire model

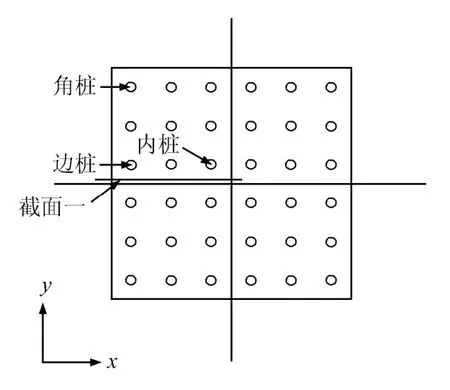
图3 承台、桩位平面图 Fig.3 Layout of piles and pile caps

2.3 计算参数

本文收集了ABAQUS中Mohr-Coulomb 模型参数的部分经验值，这些经验值选自文献[4]算例提供的经验值。本文所采用的计算参数是参考这些经验值并作调整而得到的，如表1 所示。

表1 土的Mohr-Coulomb 模型参数 Table 1 Mohr-Coulomb model parameters of soil

承台、桩身、地下连续墙混凝土的弹性模量Ec= 30 GPa，泊松比μ=0.2。地下连续墙厚度t =1 m，插入比为1：1。基坑深度为8 m。承台厚度为2 m，设9 根圆桩，桩长为50 m，桩径为1 m，桩间距为4 m。

2.4 模拟步骤

根据基坑开挖实际施工过程，对于开挖深度为8 m 的工况，在有限元模拟时分为以下8 个分析步：

（1）施加土体、地下连续墙、桩体的自重，建立初始地应力场，平衡地应力；

（2）开挖第1 层土，深度为-2 m，简称“开挖1”；

（3）激活第1 道支撑，对地下连续墙施加水平支撑力；

（4）开挖第2 层土，深度为-5 m，简称“开挖2”；

（5）激活第2 道支撑，对地下连续墙施加水平支撑力；

（6）开挖第3 层土，深度为-8 m，简称“开挖3”； （7）激活筏板，施加筏板自重；

（8）在筏板上施加均布荷载，对桩基加载。

3 计算结果分析

3.1 桩顶Q-s 曲线

桩筏基础的桩顶反力分布直接影响到筏板的内力大小和筏板厚度的确定，图4 为36 根群桩的各桩Q-s 曲线，由图4 可知：

（1）角桩出现拐点前，各桩桩顶Q-s 曲线由上至下的顺序均为角桩、边桩、内桩。角桩出现拐点后，角桩曲线发生陡降，边桩桩顶反力变成最大，各桩桩顶Q-s 曲线由上至下的顺序均为边桩、角桩、内桩。这是由于拐点的出现标志着桩-土界面发生相对滑移，角桩桩侧摩阻力达到极限状态，桩周土逐渐屈服，角桩刺入沉降增加，荷载向边桩和内桩转移，使边桩桩顶反力超过角桩。

（2）在整个加载过程中，角桩和边桩均达到极限状态，但内桩承载力远远未发挥。这是由于内桩处于群桩的包围中，桩体的夹带作用使桩-土相对位移发展缓慢，界面上的摩擦力无法充分发挥，而角桩和边桩位于群桩外侧，受群桩影响相对较少，角桩桩-土相对位移发展最快，边桩其次，能充分发挥其摩擦力。

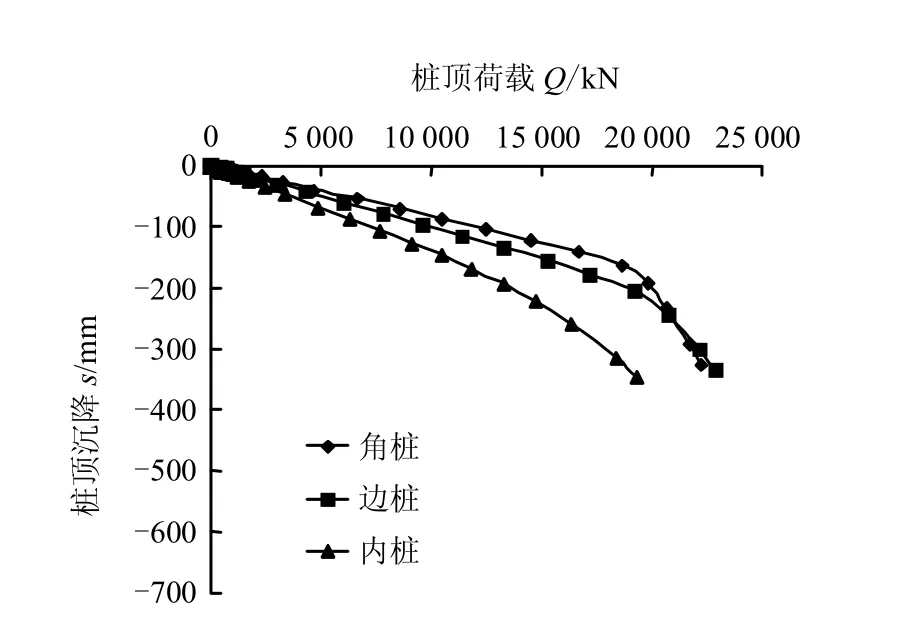
图4 各桩Q-s 曲线 Fig.4 Q-s curves for piles

3.2 桩身轴力分布

桩身轴力分布曲线实质上反映了桩的荷载传递方式。图5、6 分别是角桩在开挖和加载阶段的轴力分布图，从图可知：

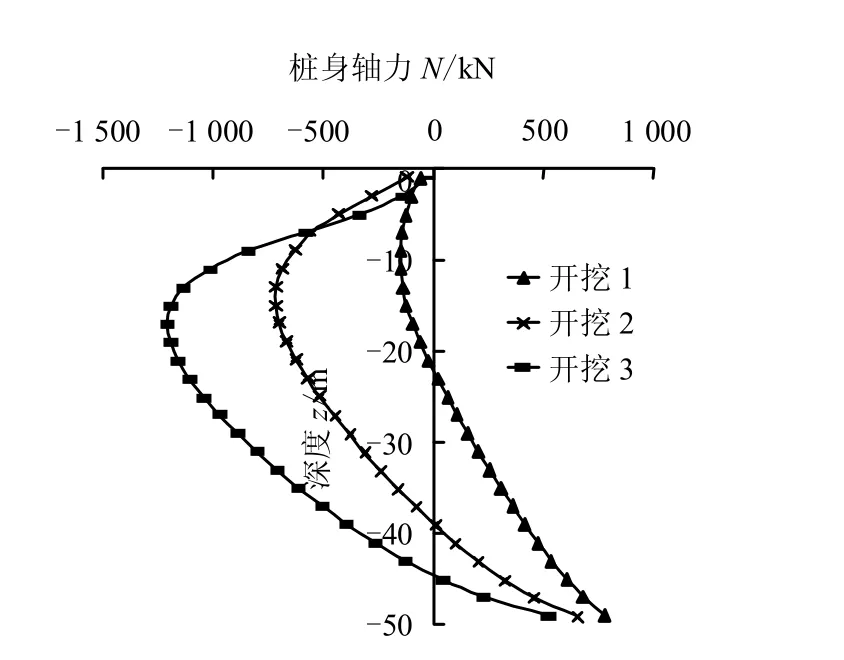
图5 开挖阶段角桩的轴力分布 Fig.5 Distributions of axial force of the corner pile during excavation

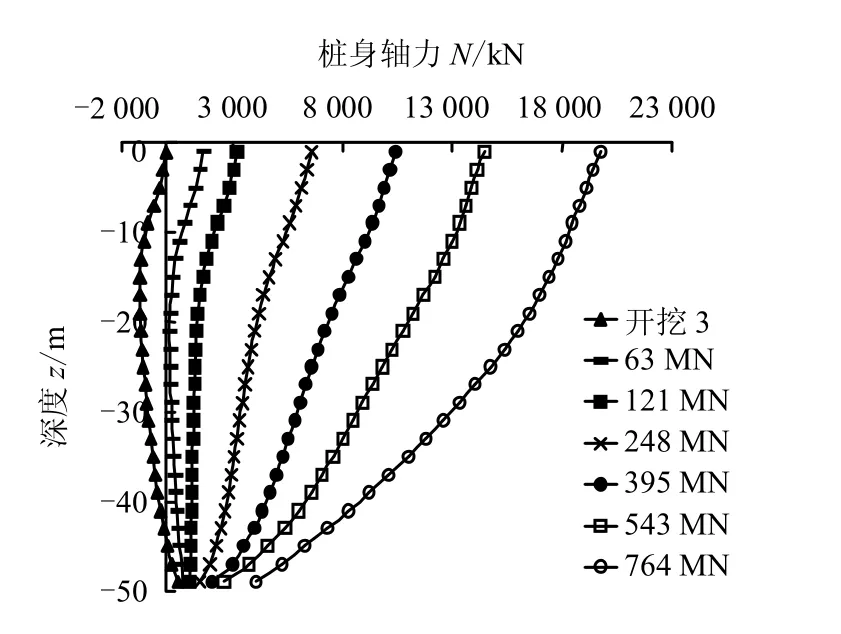
图6 加载阶段角桩的轴力分布 Fig.6 Distributions of axial force of the corner pile during loading

（1）桩身轴力分布曲线的倾斜程度大致反映桩侧摩阻力的大小，轴力曲线倾斜程度越大，侧摩阻力越大。在开挖阶段，各桩轴力分布大体相同，桩身上部受拉，下部受压。随着开挖的进行，桩身受拉区的范围不断扩大，中性点不断下移，桩身压力不断减小，拉力不断增大，各桩轴力分布曲线越来越缓，开挖进行到最后时，仅桩端部分处于受压状态。因此，在灌注桩设计施工时，桩体下部的钢筋不能随意减少，以免发生破坏，影响承载力。

（2）在加载阶段，随着桩基总荷载的增加，各桩桩身轴力不断增加，桩身受拉区迅速向受压状态变化。随着荷载增加桩侧摩阻力不断向下发展，直到发挥到极限。此后，荷载主要由端阻力来承担，端阻力不断大幅增加。总体上，荷载由侧阻和端阻共同承担，侧阻占主要，表现为端承摩擦桩。

3.3 桩侧摩阻力分布

群桩基础各桩桩侧摩阻力的大小决定了整个基础的承载能力。图7、8 分别是角桩在开挖和加载阶段的桩侧摩阻力分布图。从该图可知：

（1）在开挖阶段，桩身上部受正摩阻力，桩身下部受负摩阻力，并且随着开挖的进行都不断增加。在加载阶段，桩侧摩阻力分布由开挖阶段的“P”形向“R”型发展，最后侧摩阻力完全发挥，近似于三角形。由于开挖导致桩体上部侧摩阻力提前发挥并达到极限，所以随着加载的进行，上部达到极限的部分桩体发生整体刺入，尽管桩-土相对位移很大，但侧摩阻力保持极限值不变，桩侧摩阻力由桩身中部和下部开始发挥，桩-土相对位移增加，正摩阻力增加，负摩阻力减小，变成正摩阻力，并不断增大达到极限状态，但这将需要更多的桩-土相对位移。

（2）桩侧摩阻力无论在开挖还是加载阶段，均为异步发挥过程，即上部土层的侧摩阻力先于下部发挥，上部土层侧摩阻力先达到极限，趋于不变，而下部侧摩阻力还未完全发挥作用。随着荷载的增加，筏板对承台下土体的压缩，导致桩-土界面法向应力增大，使上部侧摩阻力的极限值增大，出现上部侧摩阻力二次发挥的现象。

（3）尽管在开挖阶段会使桩体上部的侧摩阻力提前发挥，但由于桩体下部存在与之相对的负摩阻力，在随后加载过程中，需要加载到一定值才能消除负摩阻力区，使桩身整体受压，所以桩体上部的侧摩阻力提前发挥并不会大幅降低桩的承载能力，但会影响桩侧摩阻力的发展趋势，从而影响桩的抗压刚度。

3.4 开挖引起的桩身轴线水平位移及弯矩

由图3 可知，角桩和内桩的位移具有对称性，故主要分析角桩、边桩及内桩在X 方向的位移及其弯矩。

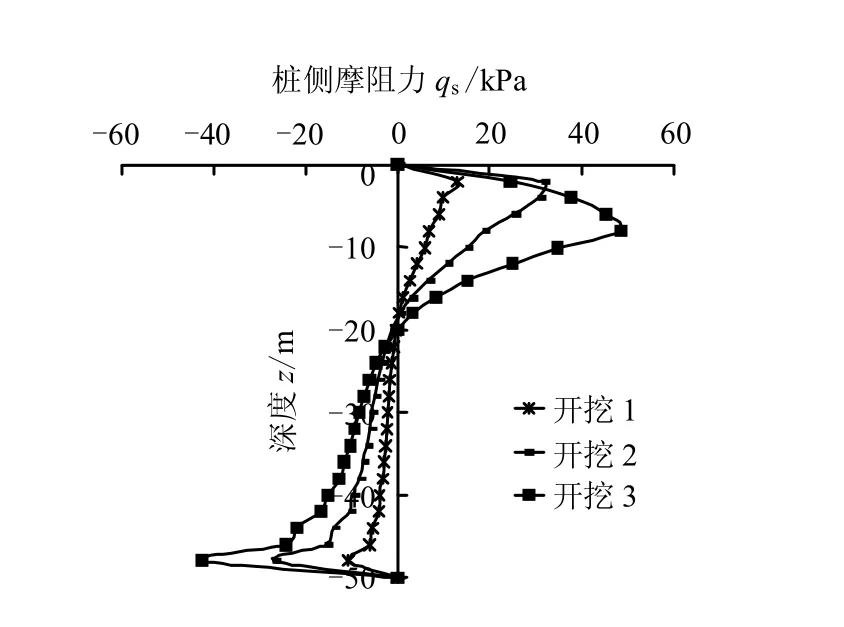
图7 开挖阶段角桩桩侧摩阻力分布 Fig.7 Distributions of side friction of the corner pile during excavation

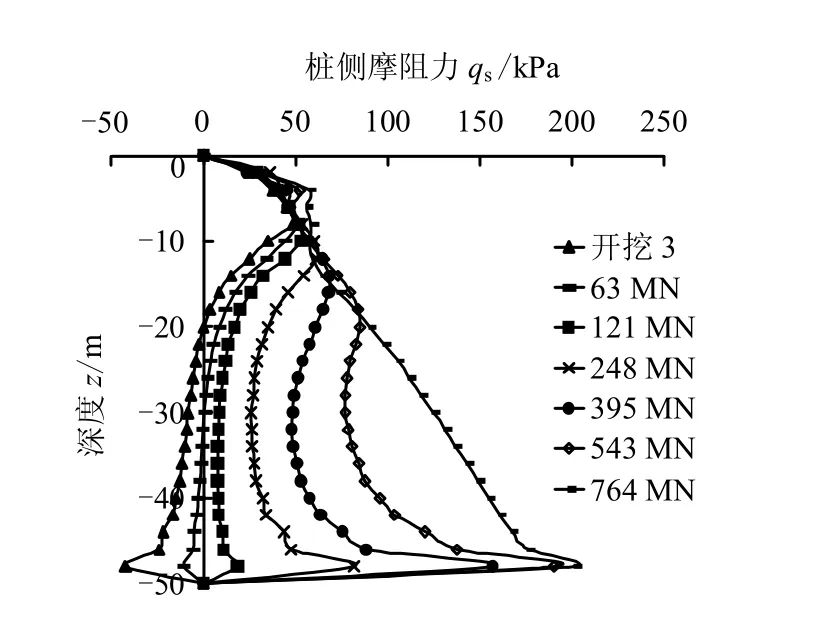
图8 加载阶段角桩桩侧摩阻力分布 Fig.8 Distributions of side friction of the corner pile during loading

图9～13 给出各桩在开挖过程中桩身轴线水平位移分布图及其弯矩图，从图可知：

（1）在开挖过程中，各桩发生向坑内方向的水平位移。总体上看，桩身上部位移最大，下部次之，中部最小，位移主要发生在桩身上部20 m 的范围内。

相对基坑开挖深度来讲，开挖的平面尺寸较大，导致工程桩下部土体也受到影响；加之工程桩较长，相当于柔性长桩，故桩身轴线挠曲呈现出反弯现象，使得桩端水平位移大于桩身中下段水平位移。

（2）在“开挖1”时，桩身轴线呈“C”型；随着开挖进行，各桩桩身位移不断增大，桩顶处出现位移回收的现象，桩身轴线向“S”型发展，桩身最大位移位置不断下移。因为随着开挖的进行，土体最大水平位移的位置沿地下连续墙不断下移，故桩侧土体对桩身侧向挤压最严重的区域也随之下移，而桩顶自由，其下部受挤压作用时向相反方向运动。

（3）由于桩身轴线的弯曲，各桩在开挖过程中产生附加弯矩，弯矩的大小受轴线弯曲程度的直接影响。弯矩主要出现在桩身上部20 m 范围内，最大值出现在-7 m 左右的位置，自由端弯矩为0。

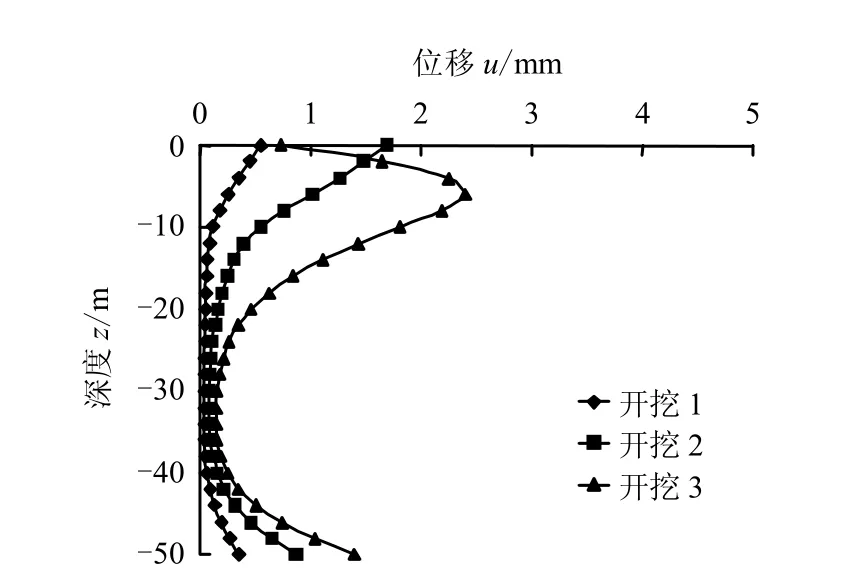
图9 角桩X 方向位移分布 Fig.9 Displacements of the corner pile in X-axis direction

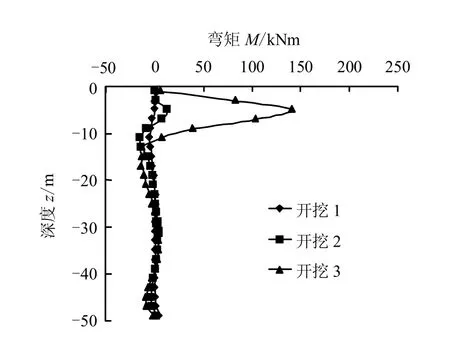
图10 角桩绕Y 轴弯矩分布 Fig.10 Moments of the corner pile around Y-axis

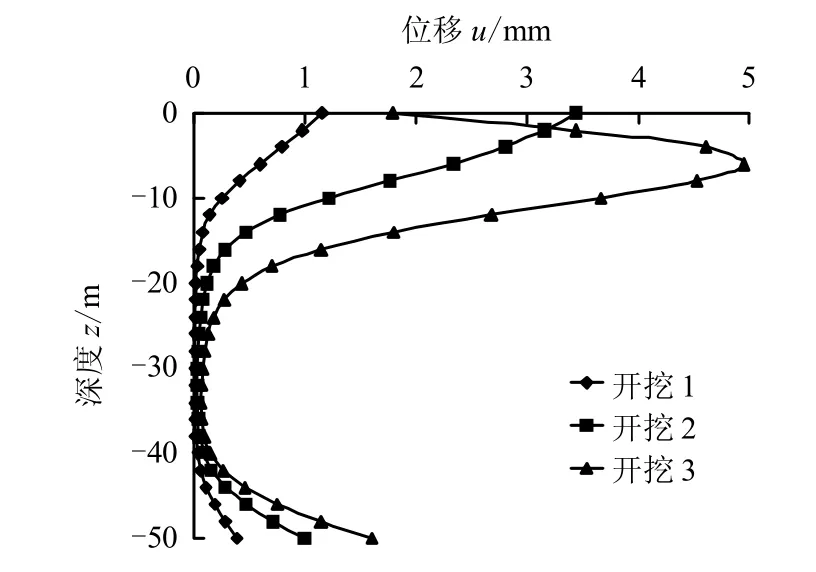
图11 边桩X 方向位移分布 Fig.11 Displacements of the edge pile in X-axis direction

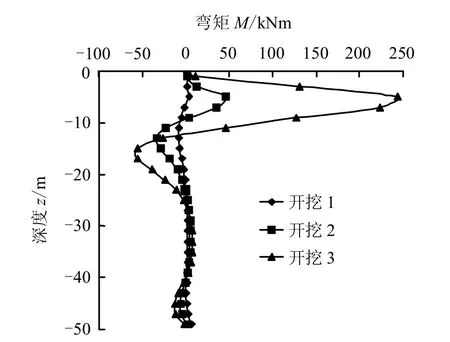
图12 边桩绕Y 轴弯矩分布 Fig.12 Moments of the edge pile around Y-axis

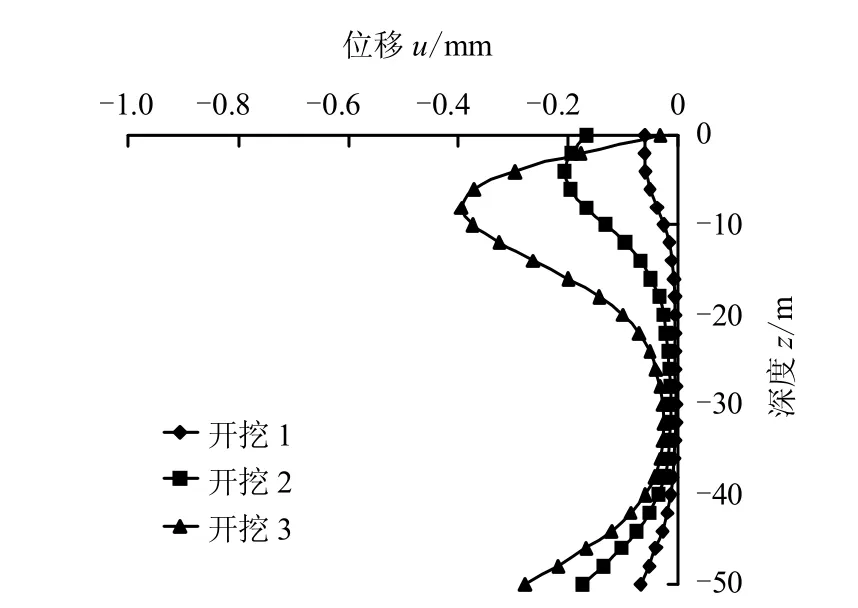
图13 边桩Y 方向位移分布 Fig.13 Displacements of the edge pile in Y-axis direction

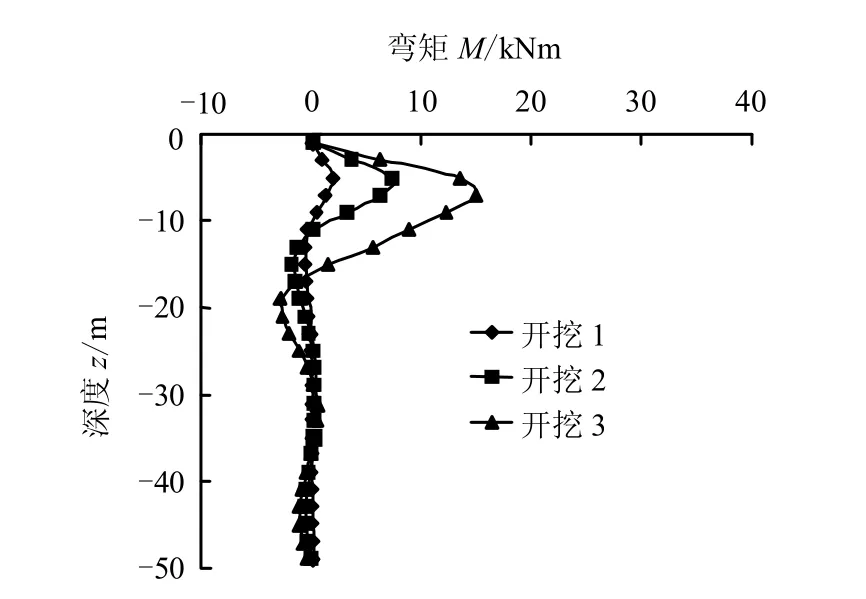
图14 边桩绕X 轴弯矩分布 Fig.14 Moments of the edge pile around X-axis

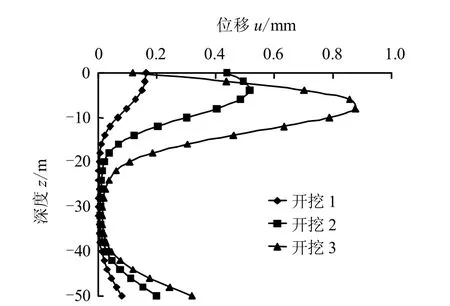
图15 内桩X 方向位移分布 Fig.15 Displacements of the inside pile in X-axis direction

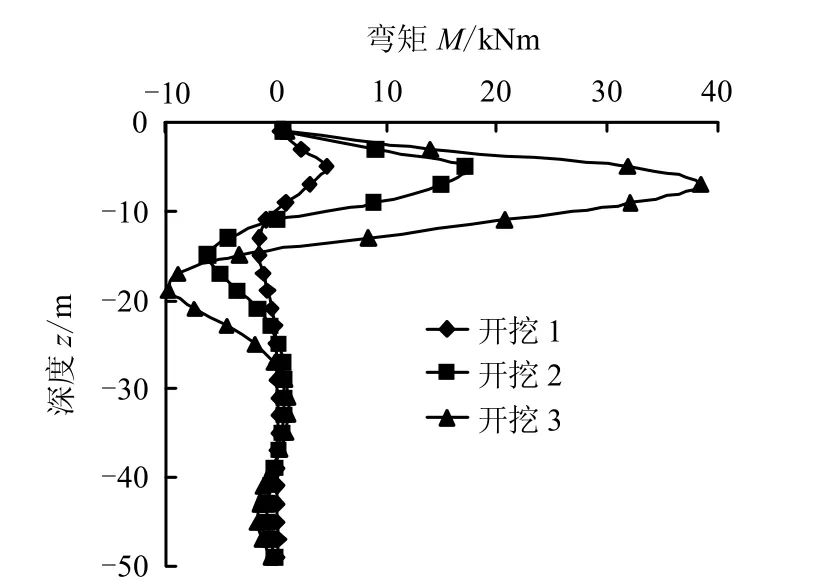
图16 内桩绕Y 轴弯矩分布 Fig.16 Moments of the inside pile around Y-axis

（4）不同位置的桩，由于其桩-土相互作用明显不同，导致桩身内力和位移差别很大。当开挖到相同深度时，桩身轴线位移和弯矩数值依次都是边桩X 方向大于角桩X 方向大于内桩X 方向大于边桩Y方向。说明基坑边沿处水平位移大，基坑中心附近水平位移小，基坑转角附近的水平位移要比同一条直线上的基坑边沿的水平小。

3.5 与不考虑开挖情况的对比

通过上面的分析，发现基坑开挖对群桩桩顶反力分布、桩身轴力、桩侧摩阻力等均有不同程度影响。本节将以前述模型为基础，去掉其中的开挖分析步，建立不考虑开挖过程的模型，仅就桩侧摩阻力进行考虑开挖与不考虑开挖情况的对比分析。

图17（a）、（b）分别是不考虑开挖和考虑开挖情况的角桩在加载过程中的桩侧摩阻力分布图。由图17（a）、（b）的对比可知，随着桩顶荷载的施加，不考虑开挖情况的桩侧摩阻力从桩身上部向桩身下部发挥；考虑开挖工况的桩侧摩阻力从桩身中部开始向桩身下部发挥，这是桩受荷前期开挖导致的初应力效应；基桩的极限摩阻力分布类型差别不明显。

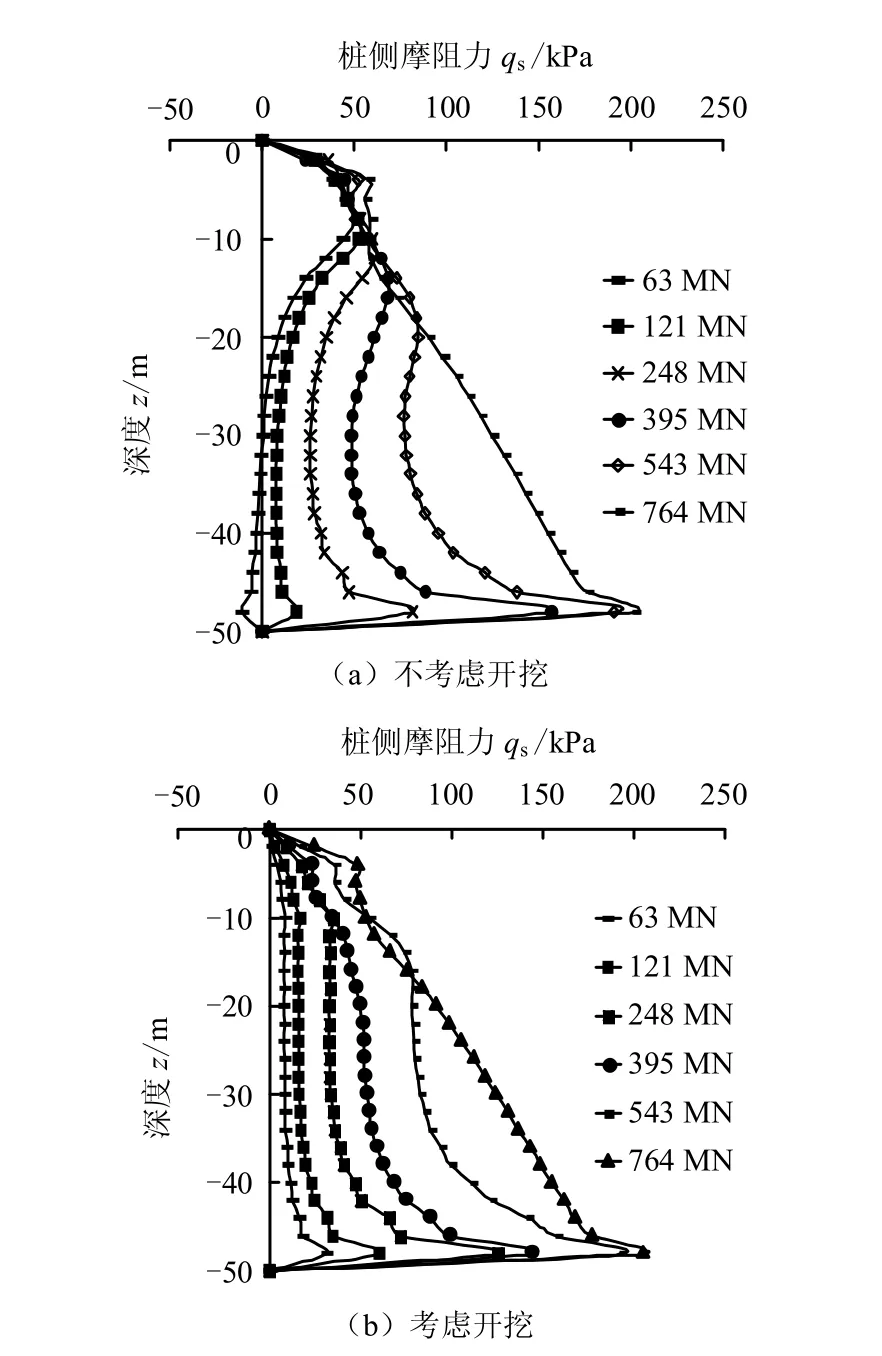
图17 考虑与不考虑开挖时角桩侧摩阻力分布 Fig.17 Distributions of lateral frictions of the corner pile, considering and without considering excavation

4 结 论

（1）基于建立的桩筏基础—地基—基坑开挖三维有限元分析模型，对基坑开挖影响下的群桩基础竖向承载性状进行了分析，得出了桩顶反力分布、桩身轴力、桩侧摩阻力以及开挖引起的桩身水平位移及弯矩的变化规律。在此基础上，对考虑基坑开挖与不考虑基坑开挖的群桩基础竖向承载性状进行了对比分析。

研究结果表明，群桩竖向承载性状受到基坑开挖过程的影响，主要表现在以下几个方面：

①在开挖完成后，各桩桩身大部分处于受拉状态，桩端附近受压。

②在开挖阶段，桩身上部受正摩阻力，桩身下部受负摩阻力，并且随着开挖的进行不断增加；在加载阶段，各桩桩侧摩阻力分布由开挖阶段的“P”形向“R”形发展，最后侧摩阻力完全发挥，近似于三角形。

③在开挖过程中，各桩发生向坑内方向的水平位移，位移和由此产生的弯矩主要发生在桩身上部20 m 范围内。随着开挖的进行，各桩位移和弯矩不断增加，且数值都依次是边桩X 方向大于角桩X 方向、大于内桩X 方向、大于边桩Y 方向。因此，在软土地区进行深基坑开挖时，坑底工程桩要考虑软黏土侧向流动的影响。

④随着加载的进行，不考虑开挖工况的桩侧摩阻力从桩身上部向桩身下部发挥；考虑开挖工况的桩侧摩阻力从桩身中部开始向桩身下部发挥。

（2）虽然限于数值分析条件和计算能力，本文计算的基坑开挖与桩基础的规模与实际工程有差距，但通过本文的研究，初步取得了基坑开挖对高层建筑桩筏基础影响的一些基本认识，这些认识对于改进桩筏基础设计理论有一定的参考意义。

[1] 胡琦， 凌道盛， 陈云敏， 等. 深基坑开挖对坑内基桩受力特性的影响分析[J]. 岩土力学， 2008， 29(7)： 1965－1969. HU Qi， LING Dao-sheng， CHEN Yun-min， et al. Study of loading characters of pile foundation due to unloading of deep foundation pit excavation[J]. Rock and Soil Mechanics， 2008， 29(7)： 1965－1969.

[2] 朱火根， 孙加平. 上海地区深基坑开挖坑底土体回弹对工程桩的影响[J]. 岩土工程界， 2005， 8(3)： 43－46. ZHU Huo-gen， SUN Jia-ping. The impact of bottom plies due to unloading of deep foundation pit excavation in Shanghai[J]. Geotechnical Engineering World， 2005， 8(3)： 43－46.

[3] 徐情根， 徐醒华， 梁朝晖， 等. 深基坑开挖对坑底桩基的影响[J]. 广东土木与建筑， 2006， 1： 33－34. XU Qing-geng， XU Xing-hua， LIANG Zhao-Hui， et al. Study on pile foundation due to unloading of deep foundation pit excavation[J]. Guangdong Architecture and Civil Engineering， 2006， 1： 33－34.

[4] 王金昌. ABAQUS 在土木工程中的应用[M]. 杭州： 浙江大学出版社， 2006. GAO Meng， GAO Guang-yun， YANG Cheng-bin， et al. Analytical solution for settlement of group piles in layered ground based on shear displacement[J]. Rock and Soil Mechanics， 2010， 31(4)： 1072－1077.

[7] POULOS H G， DAVIS E H. The settlement behavior of single axially loaded incompressible piles and piers[J]. Geotechnique， 1968， 18(3)： 351－371.

[8] MATTES N S， POULOS H G. Settlement of single compressible pile[J]. Journal of the Soil Mechanics and Foundations Division(ASCE)， 1969， 95(1)： 189－207.

[9] 吕凡任， 陈云敏， 梅英宝. 一种基于Mindlin 解的直桩沉降弹塑性分析方法[J]. 岩石力学与工程学报， 2004， 23(17)： 2988－2991. LÜ Fan-ren， CHEN Yun-min， MEI Ying-bao. Elasto-plastic analysis method for vertical pile based on Mindlin’s solution[J]. Chinese Journal of Rock Mechanics and Engineering， 2004， 23(17)： 2988－2991.

[10] SEO H， PREZZI M. Analytical solutions for a vertically loaded pile in multilayered soil[J]. Geomechanics and Geoengineering， 2007， 2(1)： 51－60.

[11] SEO H， BASU D. Load-settlement response of rectangular and circular piles in multilayered soil[J]. Journal of Geotechnical and Geoenvironmental Engineering， 2009， 135(3)： 420－430.

[12] GIBSON R E. Some results concerning displacements and stresses in a non-homogeneous elastic half-space[J]. Geotechnique， 1967， 58(17)： 58－67.

[13] POULOS H G. Settlement of single piles in non-homogeneous soil[J]. Journal of Geotechnical Engineering Division, ASCE， 1979， 105(GT5)： 627－641.

[14] GUO W D， RANDOLPH M F. Vertically loaded piles in non-homogeneous media[J]. International Journal for Numerical and Analytical Methods in Geomechanics， 1997， 21(8)： 507－532.

[15] GUO W D. Vertically loaded single piles in Gibson soil[J]. Journal of Geotechnical and Geoenvironmental Engineering， 2000， 126(2)： 189－193.

[16] 王旭东， 刘宇翼， 宰金珉， 等. 广义Gibson 地基中单桩-土-承台共同作用简化分析[J]. 岩土工程学报， 2008， 30(7)： 953－958. WANG Xu-dong， LIU Yu-yi， ZAI Jin-min， et al. Simplified analysis for interaction of single pile-soil-cap in generalized Gibson soil[J]. Chinese Journal of Geotechnical Engineering， 2008， 30(7)： 953－958.

[17] 肖洪天， 岳强， 岳中琦. 轴向荷载作用下非均匀地基中单桩及群桩分析[J]. 工程力学， 2009， 26(2)： 163－167. XIAO Hong-tian， YUE Qiang， YUE Zhong-qi. Aanlysis of axially loaded single pile and pile group in non-homogeneous soil[J]. Engineering Mechanics， 2009， 26(2)： 163－167.

[18] ZHANG Lian-yang. Nonlinear analysis of torsionally loaded piles in a two-layer soil profile[J]. International Journal of Geomechanics， 2010， 10(2)： 65－73.

[19] TIMOSHENKO S P， GOODIER J N. Theory of elasticity (3rdedition)[M]. Beijing： Tsinghua University Press， 2004.

[20] 史佩栋. 实用桩基工程手册[M]. 北京： 中国建筑工业出版社， 1999.