半金属元素掺杂TiN的第一性原理研究

薛凤英，王海媛，李德军

（天津师范大学 物理与电子信息学院，天津 300387）

半金属元素掺杂TiN的第一性原理研究

薛凤英，王海媛，李德军

（天津师范大学 物理与电子信息学院，天津 300387）

基于密度泛函数理论，采用广义梯度近似方法，对半金属元素原子X（X＝B、Si、Ge、As、Sb和Te）掺杂TiN体系的平衡晶格常数和电子结构等进行第一性原理计算，并对掺杂前后的电子态分布变化和形成能进行分析计算.结果表明：掺杂体系中主要的电子贡献仍是N2p态和Ti3d态，随着半金属元素B、Si、Ge、As、Sb和Te的掺入，TiN掺杂体系的导电性能有所提高，但并未超过纯净TiN体系；同时由形成能的计算证明Si掺杂体系最容易达到稳定结构，而Te掺杂是最不稳定的体系.

TiN；半金属元素掺杂；晶格常数；态密度；形成能

氮化钛（TiN）是一种新型陶瓷材料，具有高强度、高硬度、耐高温、耐酸耐碱、耐腐蚀、抗热震、密度低、耐磨损、良好的导电性和导热性能等诸多优良的物理化学性能［1－3］，且因具有诱人的金黄色而被广泛应用于制造坩埚、切削刀具和装饰建材表面所用的仿金材料.目前，国际上对TiN掺杂的研究较多［4－7］，但对于半金属元素掺杂情况的理论研究还未见报道.第一性原理的基本思想是将由多原子构成的体系理解为由电子和原子核组成的多粒子体系，并根据量子力学基本原理最大限度地对问题进行“非经验性”处理.基于密度泛函理论（Density Functional Theory，DFT）［8］的平面波赝势方法从第一性原理出发，通过CASTEP程序软件包［9］计算晶体模型的总能量和总能量之差，并通过体系的总能量和总能量之差获得晶体的物理和化学特性，如在体系能量最低的平衡态，可以获得晶体的晶格常数；通过计算体系总能量的变化，可以得到晶体表面能、表面吸附原子、分子的粘附能、形成能和弹性常数等.

本研究应用CASTEP软件包，采用广义梯度近似［10］对 TiN的半金属元素X（X＝B、Si、Ge、As、Sb和Te）掺杂系列进行晶格常数和形成能的计算研究，以期对过渡金属氮化物掺杂体系相关性质的理论研究进行有益补充.

1 模型和方法

本研究的计算工作由基于密度泛函理论的从头算量子力学程序CASTEP完成，采用超软赝势（Ultrasoft pseudo－potential）［11－12］描述离子实与价电子之间的相互作用，电子间交换关联能泛函选取广义梯度近似（Generalized Gradient Approximation，GGA）表征中的PBE形式［13］，通过收敛测试最终选取截断能为310 eV，布里渊区积分采用6×6×2的k点网格.自洽计算时，原子总能量的收敛值设为2.0×10－5e V.

理想TiN晶体是NaCl结构，空间群为FM－3M，α＝β＝γ＝90°，属于面心立方结构.本研究在TiN原胞的a、b和c基矢方向分别扩展1个单位，得到2×2×2的超晶胞，每个超晶胞共含有35个原子，其中8个为N原子.NaCl结构的对称性决定了原子替代位置的不可重复性.由于4种不同位置和4种不同浓度的计算结果相同，因此，本研究选取1个简单的替代位置进行计算，其中心坐标（0.5，0.5，0.5）处的Ti原子由1个半金属元素原子X（X＝B、Si、Ge、As、Sb和Te）取代，分子式为Ti26X1N8，其中杂质离子浓度为2.86%，而杂质原子的位置和晶格常数允许被改变.参与计算的价态电子为 Ti（3s2 3p6 3d2 4s2）、N（2s2 2p3）、B（2s2 2p1）、Si（3s2 3p2）、Ge（4s2 4p2）、As（4s2 4p3）、Sb（5s2 5p3）和Te（5s2 5p4），晶胞掺杂结构如图1所示.

图1 TiN 2×2×2超晶胞掺X（X＝B，Si，Ge，As，Sb和Te）的结构图Fig.1 Structure of TiN 2×2×2 supercell doped X（X＝B，Si，Ge，As，Sb，Te）

2 结果和分析

2.1 晶格常数

密度泛函理论具有1个一般规律，即由GGA计算得到的能隙和晶格常数比由局域密度近似（Local Density Approximation，LDA）计算得到的结果大，但GGA在计算总能、电离能和电子亲和力等方面较LDA优越［14］.因此，本研究选取GGA对理想TiN单胞进行优化，计算得到晶格常数为0.425 2 nm，与实验值（aTiN＝0.423 7 nm［15］）吻合较好，最大误差率约为0.7%，在允许范围内.对比掺杂半金属元素原子X（X＝B、Si、Ge、As、Sb和Te）的TiN 2×2×2超晶胞结构和未掺杂TiN超晶胞结构，晶格常数变化如表1所示.

表1 掺杂不同元素后TiN超晶胞的晶格常数Tab.1 Lattice constants for TiN supercell and TiN supercell doped different atoms

由表1可知，掺入B、Si、Ge和As后，晶胞参数虽略有减小，但整体呈增长趋势，直至接近纯TiN晶格常数；掺入Sb和Te后，TiN的晶胞参数略大于纯TiN.这是由于晶体晶胞中的原子被离子半径大的原子取代会导致晶胞膨胀和晶胞体积增大，而被半径小的原子取代则会导致晶胞收缩和晶胞体积减小［16］.B、Si、Ge和As的离子半径小于Ti的离子半径（0.060 5 nm），而Sb和Te的离子半径大于Ti的离子半径，用离子半径小的离子取代离子半径大的离子，晶胞体积也会相应减小，反之亦然，所以掺杂后TiN的晶格常数呈现出以Sb元素为分水岭，上小下大的变化趋势.这一点从它们形成的键长可以看出，本研究从固定角度获取N原子与各掺杂原子之间的键长，表1中数据显示掺入的各杂质原子和N原子之间的键长与它们离子半径的变化趋势一致，这不仅证明了上面的分析结果，也进一步验证了本研究计算结果的可靠性.

2.2 电子结构

2.2.1 未掺杂TiN的电子结构

图2为计算所得的TiN的能带和总态密度图.能带图中费米能级和导带相交以及总态密度图中态密度跨过费米能级证明TiN材料呈现一定的金属性.态密度图中，费米能级两侧分别有2个尖峰，并且2个尖峰之间的态密度不为零，与能带图较为符合，这说明化合物中金属原子和N原子之间形成了较强的共价键，从而形成所谓的赝隙，而赝隙的出现有利于结构的稳定.

图2 纯TiN的能带结构和总态密度Fig.2 Band structure and TDOS for pure TiN

图3给出了－20 eV至5 eV范围内纯TiN的总态密度图（Total Density of States，TDOS）和分态密度图（Partical Density of States，PDOS），原点选取在Fermi能级，即图3中竖直虚线的位置.由图3可以看出，理想TiN晶体的电子所处能级可分为3组，即图3中标出的带1、带2和带3.图3a中，费米能级附近的带2是最高峰，其位置坐标为（－5.13，23.80），宽度约为6.85 e V，可以看出它的峰值很尖锐，显示出较强的局域性.图3b的分态密度图表明区域中主要分布着N原子的2p态和Ti原子的3d态，且N原子2p态电子为主要贡献电子态；带3宽度约为6.08 e V，主要分布着Ti原子的3d态，还有少量N原子的2p态；带1主要分布着N原子的2s态和非常少量的Ti原子3d态.费米能级附近态密度较高代表费米能级附近的电子多，导电能力强，反之导电能力弱，因此由图3可知，TiN具有较好的导电性能.

图3 纯TiN的总态密度和分态密度（－20～5 eV）Fig.3 TDOS and PDOS for pure TiN（－20－5 eV）

2.2.2 掺杂TiN的电子结构

图4和图5分别给出了－20 e V至5 e V范围内TiN掺杂系列的总态密度图和分态密度图.

图4 X（X＝B、Si、Ge、As、Sb和Te）掺杂TiN的总态密度Fig.4 TDOS for TiN doped X （X＝B，Si，Ge，As，Sb，Te）

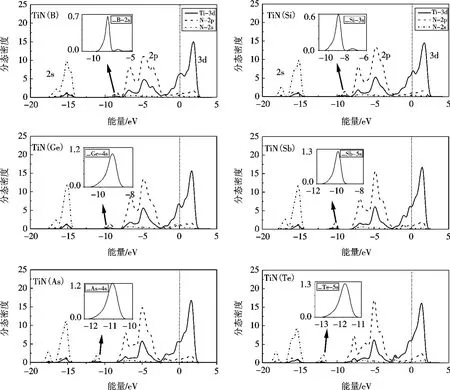
图5 X（X＝B、Si、Ge、As、Sb和Te）掺杂TiN的分态密度Fig.5 PDOS for TiN doped X （X＝B，Si，Ge，As，Sb，Te）

图4中，与图3a中对应的带2随着B、Si、Ge、As、Sb和Te原子序数的变化呈现向低能区移动的趋势，导致光学带隙宽度由6.85 eV增大到10 e V.图4中标出了与纯TiN带2最高峰相对应的峰位，坐标范围由（－4.80，15.96）至（－5.02，23.39），Te掺杂体系最高峰的峰位最接近纯TiN，但仍未超过TiN.这表明随着B、Si、Ge、As、Sb和Te原子的掺入，TiN掺杂体系的导电性能得到提高，但并没有超过纯净TiN，掺杂效果并不理想.

同时，图4中带2在向低能区扩张的过程中，边缘出现一个新的小峰，记为峰4，如图4中标出.峰4的出现可能是由于半金属元素原子掺入后，它们对态密度的贡献导致带2向低能区偏移，从而引起光学带隙宽度变大.图5对峰4所在的位置局部放大，可以看到新掺入的半金属原子确实对峰4起着大部分的贡献作用，贡献电子分别为B原子2s态、Si原子3s态、Ge原子4s态、As原子4s态、Sb原子5s态和Te原子5s态.随着原子序数的增大，电子的贡献值逐渐变大，但由于贡献力量微弱，无法改变掺杂结构的导电性能.

2.3 掺杂形成能

为了计算不同掺杂位置的稳定性，本研究分别计算了TiN各个掺杂体系的形成能，其中形成能的计算公式［17］为

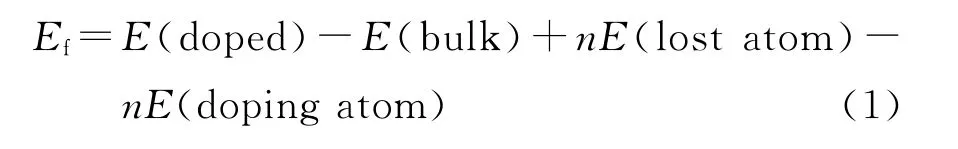
式（1）中：E（doped）和E（bulk）分别为X原子掺杂TiN和未掺杂TiN体系优化后计算得到的总能；E（lost atom）和E（doping atom）分别为被替代单原子和掺杂单原子的能量；n为掺杂原子的数目，该计算中n为1.对应到本研究计算中，式（1）变为

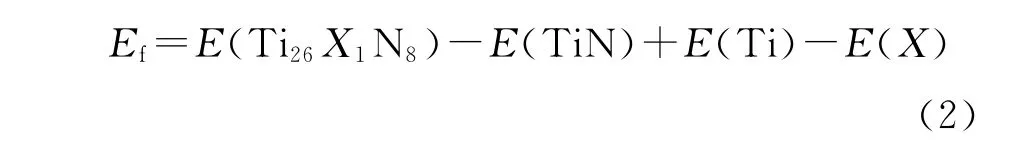
式（2）中：X＝B、Si、Ge、As、Sb和Te，纯净TiN体系计算得到的总能为－15 021.09 e V.本研究计算得到的由35个原子组成的超晶胞掺杂体系中各单原子的能量、掺杂体系总能和掺杂体系形成能如表2所示.

表2 单原子晶体能量及其掺杂体系的总能和形成能Tab.2 Total energy and formation energy for single atom crystals and their doped systems

从表2中可以看出，B、Si、Ge、As、Sb和Te单原子的能量随着原子序数的增大而逐渐减小，掺杂后TiN体系的总能也相应变小，但最终计算得到的掺杂形成能逐渐增大.其中形成能最小的掺杂体系为Si掺杂体系，仅为5.2 eV，还不到Te掺杂体系形成能（13.06 e V）的1／2.掺杂形成能越小越容易形成稳定结构，因此TiN掺杂中，Si掺杂体系最稳定，即掺杂的Si原子在理论上最容易进入晶格中，而Te掺杂是最不稳定的体系.

3 结论

本研究采用密度泛函理论平面赝势方法和广义梯度理论，对半金属元素原子掺杂TiN超胞体系进行相关的计算研究.晶格常数的计算结果与文献符合得较好，为所选计算方法的合理性提供了有效的证明；对比分析TiN体系掺杂前后的电子态密度和分态密度，得出TiN掺杂体系随着B、Si、Ge、As、Sb和Te原子的掺入，导电性能有所提高，但均没有超过纯TiN；形成能的计算结果显示形成能最小的体系为Si掺杂体系，形成能仅5.2e V，表明Si掺杂体系最稳定，最不稳定的是Te掺杂体系.

［1］ BLAHA P，SCHWARZ K.Electron densities and chemical bonding in TiC，TiN and TiO derived from energy band calculations［J］.Int J Quantum Chem，1983，23（4）：1535－1552.

［2］ AHUJA R，ERIKSSON O.Structural，elastic，and high－pressure properties of cubic TiC，TiN and TiO［J］.Phys Rev B，1996，53（6）：3072－3079.

［3］ 闵新民，邓志平，李嘉宇，等.碳化钛与氮化钛类陶瓷材料结构、性能与量子化学计算研究［J］.计算物理，1997，14（1）：1－5.

［4］ CARARA S S，THESING L A，PIQUINI P.First principles study of vacancies and Al substitutional impurities inδ－TiN［J］.Thin Solid Films，2006，515（4）：2730－2733.

［5］ ROBERT L，BRUNET N，FLAHERTY T，et al.Characterisation of TiN and carbon－doped chromium thin film coatings by acoustic microscopy［J］.Surf Coat Technol，1999（116／117／118／119）：327－334.

［6］ 陈俊英，冷永祥，杨萍，等.利用掺杂及梯度复合技术对生物材料进行TiO2（Ta～（5＋））／TiN薄膜表面改性的研究［J］.材料科学与工艺，2004，12（1）：64－66.

［7］ LOUSIL L，MAOUCHE D，ROUMILI A，et al.Pressure effect on elastic constants of some transition metals［J］.Mater Chem Phys，2005，91（1）：17－20.

［8］ KOHN W，SHAM L J.Self－consistent equations including exchange and correlation effects［J］.Phys Rev，1965，140（4）：1133－1138.

［9］ PAYNE M C，TETER M P，ALLAN D C，et al.Iterative minimization techniques for ab initio total－energy calculations：Molecular dynamics and conjugate gradients［J］.Rev Mod Phys，1992，64（4）：1045－1097.

［10］ PERDEW J P，CHEVARY J P，VOSKO S H.Atoms，molecules，solids，and surfaces：Applications of the generalized gradient approximation for exchange and correlation［J］.Phys Rev B，1992，46（11）：6671－6687.

［11］ DAVID V.Soft self－consistent pseudopotentials in a generalized eigenvalue formalism［J］.Phys Rev B，1990，41（11）：7892－7895.

［12］ LAASONEN K，PASQUARELLO A.Car－Parrinello molecular dynamics with Vanderbilt ultrasoft pseudopotentials［J］.Phys Rev B，1993，47（6）：10142－10153.

［13］ PERDEW J P，BURKE K，ERNZERHOF M.Generalized gradient approximation made simple［J］.Phys Rev Lett，1996，77（18）：3865－3868.

［14］ STAMPFL C，VAN D W C G.Density－functional calculations for III－V nitrides using the local－density approximation and generalized gradient approximation［J］.Phys Rev B，1995，59（8）：5521－5535.

［15］ 喻利花，董师润，许俊华，等.TaN／TiN和Nb N／TiN纳米结构多层膜超硬效应及超硬机理研究［J］.物理学报，2008，57（11）：7036－7068.

［16］ 董玉成，郭志友，毕艳军，等.Mg，Cd掺杂Al N电子结构的第一性原理计算［J］.华南师范大学学报：自然科学版，2009，10（3）：44－47.

［17］ HONG H L，DUAN Y F.First－principles study of magnetic properties of 3d transition metals doped in zno nanowires［J］.Nano Res Lett，2009，4（5）：480－484.

First－principles study of rare－earth elements doped TiN

XUEFeng－ying，WANGHai－yuan，LIDe－jun

（College of Physics and Electronic Information Science，Tianjin Normal University，Tianjin 300387，China）

The lattice constants and electronic structures of pure and rare－earth elementsX（X＝B，Si，Ge，As，Sb，Te）doped TiN have been studied based on the density functional theory and the generalized gradient approximation method.The change of density of state and formation energy about pure TiN and doped TiN systems have been analyzed and calculated respectively.The results indicate that the most electricity contributions in the doped system are still N2p and Ti3d states.Mixed with the rare－earth elementsX（X＝B，Si，Ge，As，Sb，Te），the conductivity of doped TiN system is improved，but not higher than that of pure TiN.The calculations of formation energy demonstrate that Si doped TiN is the most stable system，while Te doped TiN is the most unstable system.

TiN；doped；lattice constant；density of state；formation energy

O469

A

1671－1114（2012）03－0028－05

2012－02－19

国家自然科学基金资助项目（11075116）；国家重大科学研究计划资助项目（2012CB933604）；东南大学生物电子学国家重点实验室开放研究基金（2010－2012）；射线束技术与材料改性教育部重点实验室开放基金（201106）

薛凤英（1987—），女，硕士研究生.

李德军（1961—），男，教授，主要从事先进薄膜材料方面的研究.

（责任编校 亢原彬）