一种解决TSP问题的自适应协同演化计算方法
王智广,王兴会,何文俊
(中国石油大学(北京)信息工程学院,北京 102249)
演化计算来自于达尔文的自然进化理论,其通过使用种群、进化、评估、迭代等方法来体现自然界中“优胜劣汰”原则,以获得问题的最优解,常被用于组合优化问题求解.演化计算是一种非常重要的算法思想,最初由Fogel在1952年博士论文中提出,由Holland和其学生提出的遗传算法将这种思想推广并进行深度应用[1]. 目前在演化计算思想上发展出了许多算法,主要包括两个方面的内容:一种是以遗传算法、差分进化[2]、演化编程为代表的演化算法;另一种是以蚁群算法[3]、粒子群算法[4]、蜂群算法[5]为代表的群智能算法.演化算法主要以自然进化为理论依据,通过种群之间的迭代演化完成问题的求解.而群智能算法通过模拟自然界中的群智能生物(蚂蚁、大雁、蜜蜂)行为来完成问题的求解.由于两种类型的算法关注点不同,从而导致在解决问题时所产生的效果也是不同的.虽然现在没有统一的理论来规定什么样的问题适用于什么样的演化算法.但是从解决问题的实践来看,这两种类型算法具有互补性.遗传算法通过种群进行目标寻优,其强调的是全局搜索能力而对局部的细致搜索不足,而蚁群算法通过信息素的正反馈来强化局部搜索能力,但其全局搜索能力不强,而全局搜索和局部搜索不足均可能导致早熟和停滞的现象方式.因此如果能够将两种算法结合起来运行,将能够弥补各自的缺点,最大程度地避免在演化计算中经常出现的早熟、停滞现象.因此研究将这两种算法相结合的协同演化算法是目前演化计算领域重要的研究方向.Khakmardan等人[6]利用EO算法与粒子群算法相结合的方法来降低搜索过程中选入局部最优解.吴建辉等人[7]提出了一种基于竞争—合作的分层协同进化免疫算法,通过对若干个子种群进行低层免疫操作:局部最优免疫优势、克隆扩增及克隆选择算子、基于改进粒子群优化算法的抗体多样性改善和高层遗传操作:选择、抗体迁移、变异,增强优秀抗体实现亲和度成熟的机会,提高抗体群分布的多样性,以解决TSP问题.
本文提出一种自适应的协同演化方法,通过动态评估方法将蚁群算法与遗传算法有机结合起来,让两种算法相互切换运行,充分利用两种算法的各自解决问题的优点来对问题进行求解.将在下面首先介绍这两种算法的基本实现步骤,然后说明蚁群与遗传算法协同演化的方法,最后通过对TSP问题的实验测试来说明本方法在搜索速度、避免停滞、早熟等方面具有优势.
1 理论基础
1.1 蚁群算法
蚁群算法模拟了蚂蚁寻找食物的过程.每只蚂蚁在搜素食物是根据其它蚂蚁留下的信息素及自己的判断来进行搜索路径选择.每只蚂蚁在面临路径选择时,根据公式(1)来进行判断.
(1)

蚁群算法步骤如下:
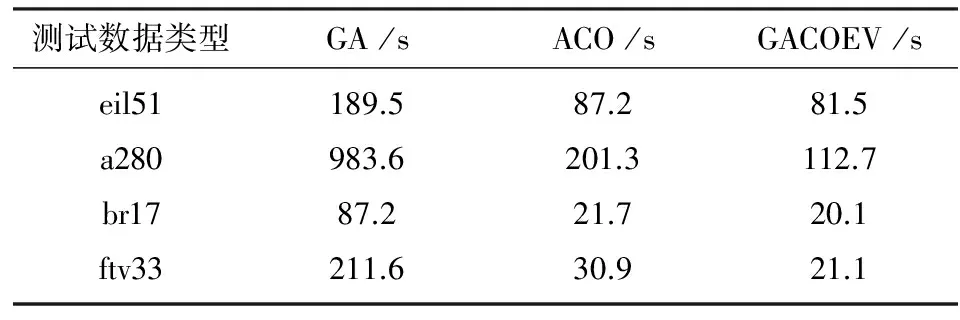
步骤1:初始化.将迭代次数g初始化为1,并初始化Mk和q0(0 步骤2:对每只蚂蚁根据公式(2)来选择节点j. (2) 其中,q是随机变量(0 步骤3:使用公式(3)和(4)更新局部信息素: (3) (4) 步骤4:对每只蚂蚁判断是否已经通过所有路径节点,如果没有通过,则返回步骤2继续执行,否则选择目前蚁群中目前的最短路径lmin. 步骤5:按照公式(5)和(6)更新全局信息素: τij=(1-λ)τij+λΔτij, (5) (6) 其中,1-λ表示全局信息素的挥发速度,Q0是常量表示全局信息素的增长速率. 步骤6:如果迭代次数超过最大限制或者已经得到合理的结果,则算法退出,否则初始化Mk(k∈m)并设置g:=g+1,返回步骤2继续运行. 遗传算法根据生物信息学中的基因编码及其进化原理得到的,其广泛应用于各种优化问题,有着很多变化的方法,但是其基本算法步骤主要包括以下几步. 步骤1:初始化种群.对种群进行相关编码,并设置迭代次数g:=1. 步骤2:根据适应度评估函数,从当前种群选择较好的m个个体. 步骤3:对此m个个体进行交叉操作. 步骤4:对交叉后的后代按照一定概率进行变异操作,并根据评估函数得到下一代种群. 步骤5:检查是否满足算法停止条件.如果满足则停止,否则返回步骤2继续运行. 在遗传算法中,如果将一个种群看作为蚁群,则种群下个体为蚁群中一只蚂蚁,算法中的交叉、变异来表示蚂蚁的路径选择动作,基于适应度评估函数的选择操作能够保存每一代蚁群之间的联系.在蚁群算法中,每只蚂蚁根据其启发函数和信息素浓度选择路径,蚁群凭借各自留下的信息素来达到协同工作的目的[8],每只蚂蚁可以表示为遗传算法中的一个个体,每一代蚁群可以表示为遗传算法中的每代种群.蚁群算法更加强调个体的搜索过程,通过遗留信息素的正反馈操作来使得蚁群协同工作.遗传算法更强调的是全局搜素能力,而蚁群算法更擅长局部搜索.因此两个算法具备可结合性和相互弥补性. 自适应协同演化方法实现的基本思路是:如果在蚁群算法中搜索的路径集中于某几条,则将搜索过程转换为遗传算法来进行;如果遗传算法出现停滞、早熟等现象,则将搜索过程转换为蚁群算法.自适应的关键是对蚁群算法和遗传算法的状态评估. 在蚁群和遗传算法运行中会出现收敛速度变慢、甚至出现停滞的现象.这是由种群的多样性趋于一致所致.因此在下面的公式分别定义了这两种算法的收敛速度、多样性的评估函数. 蚁群算法收敛速度表示为公式(8),其中D(g)表示蚁群的搜索路径结果,dk(g)表示第k个蚂蚁的搜索路径结果. (8) (9) 将蚁群的多样性使用公式(10)和(11)表示: (10) (11) 其中,Oij表示蚁群算法的第i代搜素路径结果与第j代搜索路径结果之间的差异.P(g)表示第g代蚁群搜素的路径集合. (12) (13) 自适应的选择遗传或蚁群算法运行需要对这两种算法的运行状态进行评估,根据上面定义的收敛速度及种群多样性函数,定义函数T(g)表示第g代两个算法的运行状态,如公式(14)所示. (14) 其中,g表示迭代次数,C1和C2是常量.T(g)的值为布尔类型,如果得到结果为false则当前算法继续运行,否则将选择另一个算法运行. 为使得两个算法协作运行,需要对每种算法的运行结果进行保存,当切换到另一种算法运行时,可以从前一个算法运行结果基础上继续运行.具体的模型如图1所示,两个算法的切换通过每次迭代后的评估函数T(g)来进行判断.在最优队列中保存两个算法得到的最优结果,其可以作为这两个算法被切换运行后初始化的种群.在遗传算法运行结束后需要根据结果更新蚁群的全局信息素,以保障蚁群算法运行时能够在遗传算法结果基础上继续运行. 图1 基于遗传算法和蚁群算法的自适应协同模型 为了测试此种自适应协同演化方法的有效性,针对TSP问题使用TSPLIB库进行实验测试.实验过程中使用C++语言,在CPU3.2G、内存4GB机器上实现了上述协同模型及相关算法、以及传统的蚁群算法和遗传算法,设置各个参数数据值为m=n/2,α=0.75,β=0.72,q0=0.81,Q=2000,Q0=1800,ρ=0.75,λ=0.85.而参数C1和C2取值随TSP问题规模不同,而取不同数值,通过实验测试,通常C1=n×10(n为TSP问题的节点规模), 0.03≤C2≤0.06.在设置迭代次数限制为4000代时,将实现的算法运行15次得到的平均结构如表1、表2和表3所示.在表中,TSPLIB表示测试集目前已知最优结构,GA表示遗传算法,ACO表示蚁群算法,GACOEV表示此自适应协同模型算法,eil51、lin105、a280、ftv100等表示测试数据类型. 表1 Symmetric TSP问题不同算法的数据结果比较 表2 Asymmetric TSP问题不同算法的数据结果比较 表3 不同算法的收敛时间比较 从表1~3中数据结构看,本文提出的协作演化模型方法与传统的遗传算法或蚁群算法相比具有明确的优势,得到的最优值明显好过其它两个算法,并且收效速度有着较大幅度的提高.针对a280问题,此模型方法的收敛速度约为遗传算法的9倍,蚁群算法的2倍. 针对遗传算法和蚁群算法容易产生早熟、停滞等现象,分析这两种算法的运行特点:遗传算法全局搜索能力强;蚁群算法局部搜索能力强.在此基础之上提出基于遗传算法和蚁群算法的自适应协同演化方法.通过定义种群多样性、收敛速度的判断函数以及算法运行评估函数来对目前算法运行状态进行评估,根据评估结果自动调整所要运行的算法,从而实现了遗传算法和蚁群算法的协同演化运行.从TSP问题的实验数据结果进行分析,此协同演化方法明显加快了收敛速度,提高了搜索问题的结果,并且比较好地抑制了遗传算法和蚁群算法容易产生的早熟、停止等阻碍算法继续有效率运行的现象. [1]De Jong K. Evolutionary computation: a unified approach[C]//ACM.Proceeding of the 2007 GECCO Conference Companion on Genetic and Evolutionary Computation Conference(GECCO′07).New York:ACM,2007:3158-3171. [2] Price K,Storn R M,Lampinen J A.Differential evolution: a practical approach to global optimization[M]. Berlin:Springer, 2005:13-55. [3] Dorigo M.Optimization,learning and natural algorithms[D]. PhD thesis.Italie: Politecnico di Milano, 1992. [4] Kennedy J, Eberhart R. Particle swarm optimization[C]//IEEE. Proceedings of IEEE International Conference on Neural Networks. Australia:IEEE, 1995:1942-1948. [5] Pham DT,Ghanbarzadeh A,Koc E,et al. The bees algorithm, technical note[R].UK:Cardiff University, 2005. [6] Khakmardan S, Poostchi H, Akbarzadeh M R. Solving traveling salesman problem by a hybrid combination of PSO and extremal optimization[C]//IEEE. The 2011 International Joint Conference on Neural Networks (IJCNN). California:IEEE,2011:1501-1507. [7] 吴建辉, 章 兢, 张小刚, 等. 分层协同进化免疫算法及其在TSP问题中的应用[J]. 电子学报. 2011, 39(2):336-344. [8] 朱庆保, 杨志军. 基于变异和动态信息素更新的蚁群优化算法[J].软件学报, 2004,15(2):185~192.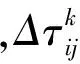
1.2 遗传算法
1.3 遗传算法和蚁群算法之间的联系
2 自适应协同演化方法
2.1 算法收敛及多样性判断
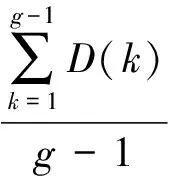



2.2 基于遗传算法和蚁群算法的自适应协同模型

3 实验测试


4 结语

