一种NTC热敏电阻校正方程的试验研究*

张鹏超，张 强

(1．陕西理工学院电气工程学院，陕西汉中723000;2．陕西理工学院机械工程学院，陕西 汉 中723000)

NTC热敏电阻器以其灵敏度高、热惯性小、受磁场影响小、抗辐射，价格低廉等优点，在实际工作中把NTC热敏电阻作为温度传感器是最为常见的。对提高NTC热敏电阻的校正方程精度的研究取得了很大的进展。从NTC制造工艺角度提高NTC热敏电阻测温的稳定性［1－2］，此方法可以保证NTC热敏电阻工作的可靠性，但是实际应用中必须对其阻温特性进行校正，常用的方法有:(1)对NTC热敏电阻进行的线性化的研究方法［3－4］，此方法误差较大，且过程复杂;(2)利用传统的经验指数校正方程进行分段多项式拟合非线性补偿的方法［5］，这种方法需要拟合出多个关系式，一旦超出拟合温度范围，精度不能保证，并且应用起来较复杂;(3)采用Steinhart-Hart方程［6－10］对 NTC 热敏电阻的 R－T 特性进行校正，但是此方法需要拟合4次，且精度不能满足高精度要求。

近年来，随着对NTC热敏电阻的测温原理研究的深入［11］，采用硬件补偿法的研究也广泛的应用起来［12］，在较小的温度范围内能够得到较高的精度补偿效果，但是超出此范围的测温精度较差且设计电路复杂，在实际应用中并不可靠;

本文在对传统的NTC指数校正方程的基础上，采用线性化变换，利用最小二乘法对实测的R－T数据进行一次、二次、三次、四次拟合，而且此方法拟合出的校正方程结构简单，并且经过误差分析和实际应用中验证了此方法能达到更高的精度。

1 数据的标定

根据实际测温需要，对NTC热敏电阻温度计在273．15 K ～373．15 K(0～100 ℃)采用恒温水箱控制温度，用安捷伦表来测量NTC热敏电阻随着温度的变化而对应的电阻值，并且用量程0～100℃的水银温度计来测量实际温度，测得的实际数据见图1。

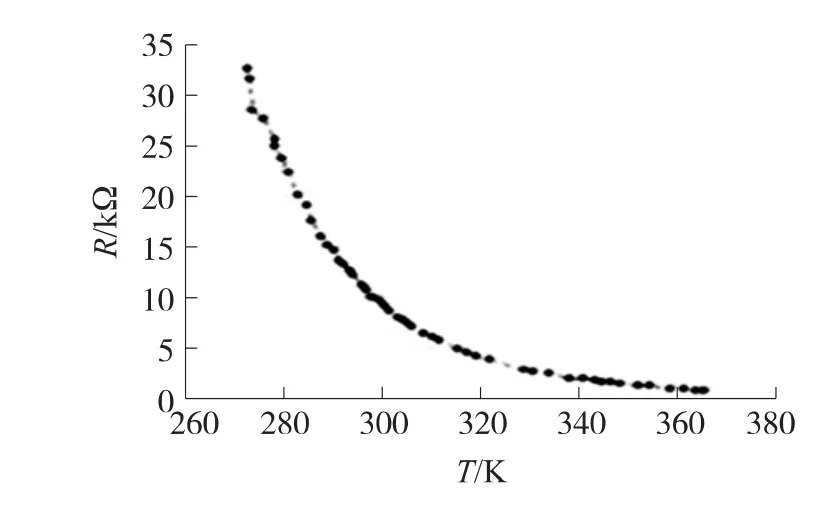
图1 10K热敏电阻温度计R－T的实测数据关系曲线

由图1可以看出NTC热敏电阻具有高度的非线性特性，且呈现出指数关系，由此引出传统的NTC热敏电阻校正方程:

式中:RT是当温度为T时的电阻值，RT0是当温度为T0时的电阻值，B是电阻热敏常数。方程(1)可以进行数据线性化变换［13］以方便拟合，转换后的表达式为:

式中:a、b为常数，设R=lnRt，式(3)可以看成T=a+b·R，由此可以看出NTC热敏电阻的R－T特性关系为一次函数关系;本文将应用最小二乘法来对式(3)分别进行一次，二次，三次，四次拟合，再利用误差评价原理评价出最适合NTC热敏电阻的校正方程。

2 基于Matlab的数据拟合方法

2．1 最小二乘法拟合的基本思想［13］

本文基于Matlab运用最小二乘法来对实测数据进行拟合:即选择一个多项式p(x)，使平方误差(在某种意义下)达到极小的方式来逼近一个已知函数，其基本思想首先为Gauss所提出，有几种版本，取决于所涉及的自变量的集合及所用的误差度量。

首先，当数据为离散时，我们可以对给定的数据xi，yi及 m＜N 将和

极小化，条件m＜N使多项式

式(5)未必能在所有N个数据点上都能匹配，故S很可能不会变成零。高斯思想是尽我们所能使S变小。经过多年得研究发展，得到了最小二乘法的另一种形式，即:

含有新系数ak，决定这些ak的方程组证明特别容易求解:

这些ak的确使误差和S极小化，极小值为

其中Wk为表达式中作为分母的和式，拟合后的方程系数如表1所示。

表1 10K热敏电阻拟合关系式系数

2．2 Matlab 实现

应用Matlab工具箱的Polyfit(R，T，n)对NTC热敏电阻的R－T特性分别进行一次，二次，三次，四次拟合或者更高次的拟合，R为lnRT值、T为实测温度值、n为最小二乘拟合次数。拟合后的方程系数已由表1所示。

2．3 误差评价原理［14］

由于本文所选用的都是经验公式，在拟合过程中对有效数字的选取，导致了试验误差的存在，尽管标定中R、T都有4位有效数字，但是必然存在试验的测量误差。所以测量值f与拟合值之间要满足下面的关系:

可以利用绝对误差、平均误差以及均方根误差来比较拟合曲线与实测数据之间的误差。

2．3．1 绝对误差:

式中:E(f)为各个校正方程的绝对误差;yk是各个关系式的拟合值;f(xk)绝对误差变化得越平稳，证明方程的精度越高。

2．3．2 平均误差:

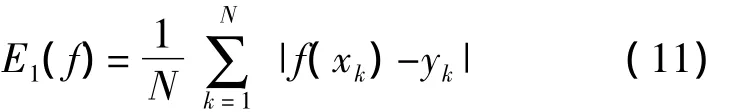
式中:E1(f)为校正方程拟合的平均误差;N为实测数据点数;式中的意义是拟合后的平均误差的绝对值求和后再求平均值，E1(f)越小，表示方程的精度越高。

2．3．3 方程有效性的评价

一组近似值Ai对相应的真值Ti的标准差定义为［14］:

E2(f)为校正方程的标准差;在Ti为已知的各种试验情况下，我们将用这个误差度量来估计最小二乘平滑化的有效性;E2(f)越小，表示方程精度越高。

2．4 评价校正方程:

通过表1的各个拟合方程的系数进行误差分析，由图2可以看出对NTC热敏电阻的R－T特性关系进行一次拟合的误差震荡比较大，对于二次，三次，四次拟合误差，不太好评价好坏，因此，对此3种拟合的平均误差及标准差进行对比，以便评价出更适合NTC热敏电阻的校正方程，见表2。

图2 四种拟合绝对误差对比

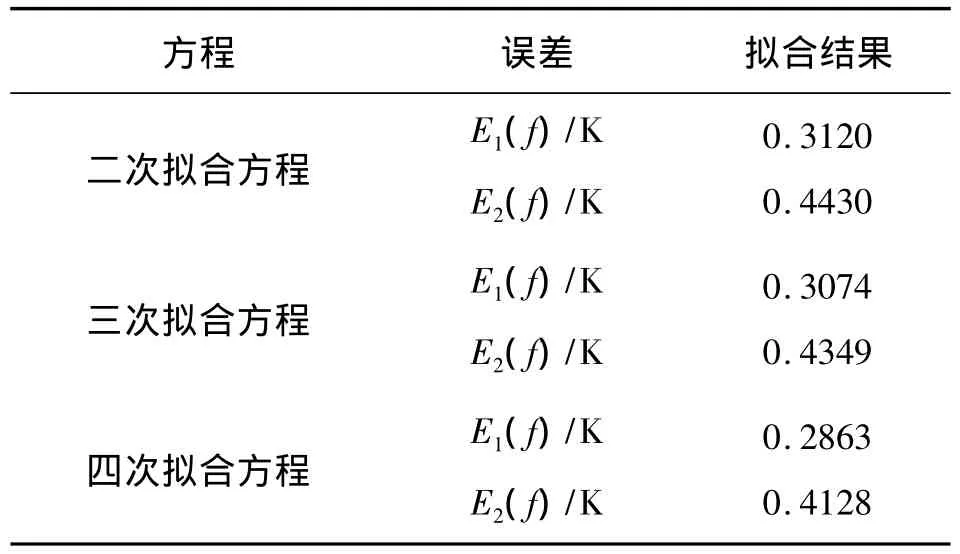
表2 10K热敏电阻4个方程拟合误差

表2中E1(f)/K为平均误差，E2(f)/K为评价方程有效性的标准差。根据误差评价原则:分别去掉一个最大误差、最小误差。由表2可以看出:四次拟合方程的E1(f)/K=0．286 3及E2(f)/K=0．412 8最小，可以看出，经过四次拟合的方程在237．15 K～337．15 K(0～100℃)范围内是最适合NTC热敏电阻温度计精度的校正方程。

3 结论

通过对传统的指数方程进行线性变换，得到一种新的NTC热敏电阻温度计R－T特性关系，对此关系进行最小二乘拟合，并进行了绝对误差，最大、最小绝对误差，平均误差的分析之后，可以看出，对于式(3)进行一次拟合得到的方程不能精确地对NTC热敏电阻温度计的非线性进行校正;通过对NTC热敏电阻温度计的R－T特性关系进行更高阶的拟合并求出各个拟合方程的标准差，比较之后得出四次最小二乘拟合的方程是最适合NTC热敏电阻温度计的校正方程，适用于NTC热敏电阻的具体校正方程如下:

实际上，由表2可以看出，对NTC热敏电阻的R－T实测数据应用最小二乘法，进行二次拟合得出的校正方程的精度已经比传统的校正方程高很多，可根据具体工况来决定选择校正方程。应用式(13)在实际的应用当中得到了很好的验证，保证精度，且测量方法简单，价格便宜，宜广泛应用，本文确定校正方程的方法适用于各类热敏电阻温度计的校正拟合。

［1］ 翟继卫，沈波，妥万录，等．热压烧结对NTC热敏电阻稳定性的影响［J］．传感技术学报，1996，1(4):32－34．

［2］ 武明堂，邓长霖，李平．(NiCo)(CoFe)系NTC热敏半导瓷新材料的研究［J］．传感技术学报，1988，1(2):33－40．

［3］ 赵军，谢作品，吴珂．NTC热敏电阻线性化新方法［J］．电测与仪表，2006，43(1):12－14．

［4］ 沙占友，王彦朋，杜之涛．NTC热敏电阻的线性化及其研究［J］．自动化仪表，2004，25(9):28－30．

［5］ 杜西亮，孙慧明，聂义祥．NTC热敏电阻器分段多项式拟合非线性补偿［J］．传感器技术，2005，24(8):13－15．

［6］ White D R．Technical Guide10-A Simple，Narrow-Band，Thermistors Themometer［M］．Measurement Standards Laboratory of New Zealand，2005．

［7］ 兰玉岐，朱晓彤，李山峰，等．低温用NTC热敏电阻校准方程的评估［J］．低温工程，2010(5):50－52．

［8］ SteinhartI S，Hart S R．Calibrationcurves for Thermistors［J］．Deep Sea Research，1968，15(3):497－503．

［9］ Lightwabe I L X．Thermistors Calibration and the Steinhart-Hart E-quation［M］．ILX Lightwate Corporation，2003．

［10］ Alexander M D，Mac Quarre K T B．Toward Standard Thermistor Calibration Method and Data Correction Spreadsheets［J］．Review of Scientific Instrument，1988，59:975－979．

［11］范寒柏，谢汉华．基于NTC热敏电阻的三种高精度测温系统研究［J］．传感技术学报，2010，23(11):1576－1579．

［12］崔文德，李铁鹏，牛建永，等．热敏电阻低温测量方法研究［J］．宇航计测技术，2010，30(4):25－31．

［13］罗亮生，包雪松，王国英．数值分析(全美经典学习指导系列)［M］．科学出版社，2002．

［14］ 周璐，陈渝，钱方，等．数值方法(MATLAB 版)［M］．4版．电子工业出版社，2005．