微机械谐振器的快速测试方法*

邢维巍，张晓灿，樊尚春，汤章阳

(北京航空航天大学仪器科学与光电工程学院，北京100191)

谐振式微传感器是基于谐振测量原理的传感器，当被测量作用到传感器上，会引起敏感元件谐振频率的变化，通过测量谐振频率的变化值，就可以得到被测量的值。谐振式微传感器具有体积小、重量轻、精度高、稳定性好的优良特性［1－2］。其中压阻检测的谐振式微传感器有体积小，结构简单，容易检测的优点，得到了广泛的应用［3－5］。但是对于微机械谐振器，其输出的信号幅度微弱，淹没在背景噪声中，需要采用微弱信号检测的方法。

现阶段一般采用的微弱信号检测方法大致分为两类［6］:锁相放大的方法和互相关检测的方法，在微电子、无线传输、图像处理、光电检测等领域，得到了广泛的应用［7－11］。国内学者针对压阻检测的微机械谐振器，提出了专用微弱信号检测方法。文献［12］中提出了一种直接相关检测的方法，与传统的锁相放大器相比，提高了信噪比;文献［13］中介绍了一种分时正交相关检测的方法，可以同时检测输出幅值和相位;这两种方法有个共同的缺点:测量时间长。由于被测对象本身存在着漂移，如果测量时间过长，会造成输出曲线失真。为了缩短测量时间，避免输出曲线失真，本文提出一种快速检测方法，减小了系统的等效输入噪声，缩短了测量时间，提高了测量效率。

1 测试方案

压阻检测的微机械谐振器检测原理是利用压阻效应将微谐振器的振动信号转化为检测电阻阻值的交变变化(其瞬时电导也是交变信号)。一般采用检测方法是给检测电阻加直流电源，将电阻阻值的变化转换成电压或者电流的变化，然后再将该电压或者电流送入乘法器中进行相敏检测。

本文提出的快速检测方法采用了文献［12］中提出的“欧姆鉴相”法。该方法以纯交流信号作为参考信号加到检测电阻上，根据欧姆定律，检测电阻输出的电压/电流信号就是参考信号与被测信号的乘积。检测电阻在将被测信号转化成电压/电流的同时，也完成了参考信号与被测信号的乘法运算。后面只需要低通滤波器或者积分器就可以提取出包含有用信号的直流分量。

与一般检测方法相比，“欧姆鉴相”方法与其他的乘法器相比，有输入动态范围大，抗干扰能力强、噪声水平低、不存在失调等优点，非常适合用于微谐振器的输出信号检测中［12］。

快速检测方法测量时采用频率扫描法［12－13］，即令参考信号和激励信号的频率从某一个频率开始，以一定的步长，到某一个频率结束。当设定的参考信号和激励信号的频率与谐振器的固有频率相同的时候，谐振器处于谐振状态，系统的输出值达到最大。当输出值达到最大时候的参考信号的频率即为谐振器的谐振频率。

2 快速检测方法理论

快速检测方法原理，如图1所示。参考电压信号Vref(t)与被测电导信号yd(t)完成乘法运算后，产生的电流信号i(t)通过积分器中做积分运算。积分电容的放电由开关控制，每次积分完成后闭合开关给积分电容放电。其中电阻R为放电电阻，积分电容C通过R放电。

图1 快速检测方法原理

2．1 被测信号

对于压阻检测的微机械谐振器，其瞬时输出是一个有偏置的交变电阻量，其瞬时电阻rD(t)的表达式为:

其中，RD为检测电阻本身的阻值;Rd为检测电阻的交流分量的幅值;ωd为检测电阻的交流分量的角频率;φd为检测电阻的交流分量的初始相位。Rd的表达式为:

εd即为检测电阻的相对变化量;因为εd≪1，故检测电阻的瞬时电导为:

其中，YD=1/RD，Yd=－YD·εd。

2．2 快速检测优化方法

当参考电压加到拾取电阻两端时，会在电阻上产生鉴相电流信号:

这里令φref=φd=0，故鉴相电流为:

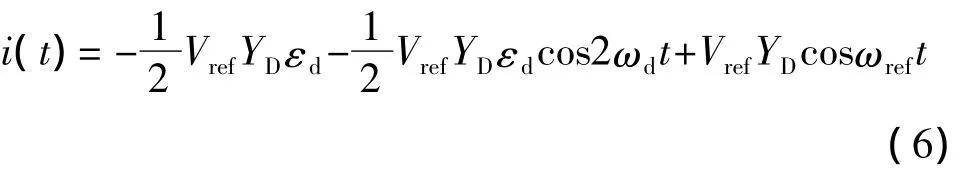
由上式可以看出，在鉴相结果中，第1项和第2项包含有用信号εd，第3项为一倍频干扰。由于有用信号εd≈10－6，故一倍频分量远大于直流分量，这里对图1的原理电路进行优化，优化后如图2所示。其中，RD为检测电阻，RM为匹配电阻，阻值与检测电阻相同。

图2 优化的快速检测方法

经过优化的快速检测方法的鉴相电流为:

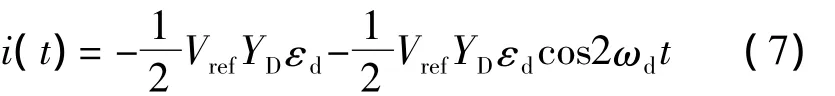
该电流通过积分器，输出信号为电压信号:

这里取积分时间 TI=kπ/ωd，k=0，1，2，3…时，系统的输出为直流分量:

这里忽略负号，若所取的积分时间越长，输出信号的直流分量越大。因此巧妙地选择积分时间TI=kπ/ωref，k=0，1，2，3…，就能够有效的消除二倍频干扰。

快速检测方法信号波形图如图3所示，其中yd(t)为检测电阻交变量的电导形式，Vref(t)为输入正弦参考电压信号，i(t)为测试系统的鉴相电流包含有用信号的部分，Vout(t)为输出电压信号。积分器工作一段时间后模拟开关闭合，对积分电容进行放电处理，输出波形如3(d)图所示，保证每次积分从零开始，防止积分结果累积造成积分器饱和。

图3 检测方法信号波形图

当选择积分时间为 TI=kπ/ωref=k/2fref，k=0，1，2，3…时闭合开关，这时候系统的残余一倍频干扰和二倍频干扰最小，有用信号的输出值最大。所以只要通过设置MCU使A/D的采样频率为参考信号频率的2倍，则所得的采样数据信噪比最高。

2．3 频率扫描方法

微谐振器振动的理论模型可由一个等效的单自由度欠阻尼系统来描述，其的归一化幅频特性为:

其中，A(ω)是微谐振器振动的幅度，ξ是系统的等效阻尼比系数，ω为频率扫描法中微谐振器的振动频率，ωn为微谐振器的固有频率。

采用频率扫描法以后，系统输出的归一化幅频特性曲线如图4所示。

测试时采用的频率扫描方法包含‘粗扫’和‘细扫’两部分。测试过程中，首先在一个较大的频率扫描范围内进行‘粗扫’，即以较大的步长进行扫描，找到谐振峰的位置，缩小频率范围;然后进行‘细扫’，即以较小的步长在缩小的频率范围内扫描，找出谐振峰对应的参考信号频率点，即为微机械谐振器的谐振频率点。

3 实验验证

基于快速互相关检测方法，设计了与之相对应的原理样机，其原理框图如图5所示，单片机控制DDS产生激励信号和参考信号，分别加到激励电阻和检测电阻上，微机械谐振器的检测电阻的阻值拾取到微谐振器的瞬时交变变化;微弱信号处理模块将微机械谐振器的电阻信号转换为电压信号并经过单片机的A/D采样并进行直线拟合，并将拟合的斜率和参考信号的频率保存下来。然后通过单片机控制DDS以一定的步长改变参考信号和激励信号的频率，并将这一系列频率点的数据保存下来，得到系统的幅频特性曲线。

图5 微机械谐振器频率特性测试样机框图

以微机械谐振器频率特性快速测试方法样机对电热激励－压阻检测的微谐振器进行测试。实验所用的微谐振器的检测电阻约为313 Ω，设置单个频率点的测量时间为4 ms。在扫描频率点一定的情况下，单个频率点的测量时间越短，系统所需的测量时间就越短，系统测量的效率就越高。

测试结果如图6所示，输出结果为通过检测电阻的电流值的大小［14－15］。由图中可以看到，测试结果的幅度最大值为4．87 nA，而图中的测试结果中的幅值不是从0开始的，这表明:测试过程中有直流偏置的存在，这里大约为0．7 nA，是由系统中积分电容的残余电荷和低频噪声产生的。由于被测量为系统的相对输出最大值时的参考信号的频率，故直流偏置不影响系统输出结果的精度，则测试的峰值幅度为4．17 nA，谐振峰幅值对应的频率约为31．52 kHz。

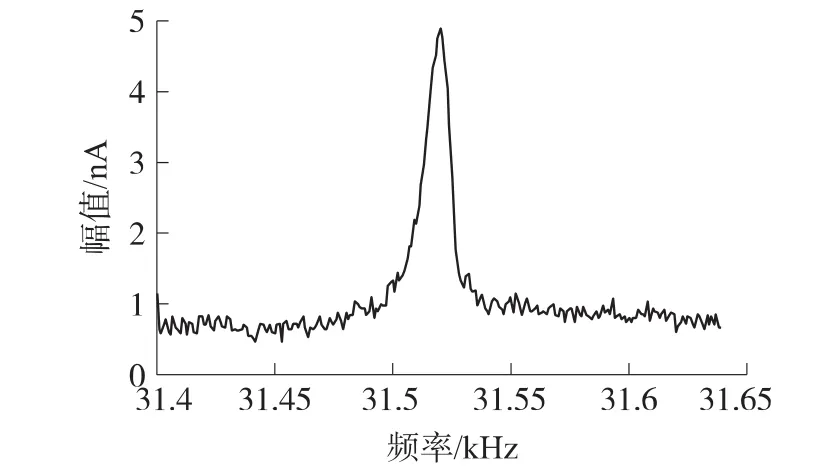
图6 微谐振器快速测试方法样机输出幅频特性

在图6中，测量所用的微谐振器Q值高至上千，这里认为:当谐振器振动频率小于31．49 kHz和大于31．56 kHz时，幅频特性曲线中有用信号近似为零。故图6中谐振峰两侧‘毛刺’是测试系统中的流过检测电阻的噪声电流，即为输入等效噪声电流，通过求均方根值，其有效值为0．03 nA，检测电阻的阻值约为313 Ω，则输入等效噪声电压约为9．39 nV。

商用锁相放大器(LIA)(型号:PerkinElmer 7265)［16］，当 R C=20 ms时输入等效噪声带宽 E NBW=12．5 Hz，其输入等效噪声指标为en=5 nV/。低通滤波器的时间常数为20 ms，则测量时间为100 ms。而当噪声带宽为12．5 Hz的时候，快速测试方法样机的输入等效噪声指标为 2 ．7 nV。

微谐振器快速测试方法样机内部电路采用了模拟信号与数字信号隔离，模拟地和数字地隔离及变压器隔离等方法减小干扰。所以当实验中单频率点测量时间取4ms时，就可以实现对微谐振器进行有效检测。微谐振器频率特性快速测试方法样机与商用LIA测量结果对比如表1所示。

表1 两种仪器指标对比

通过表1可以看出:微机械谐振器频率特性快速测试方法的等效输入噪声指标小于商用LIA，而且单一频率点的测量时间也远远小于商用LIA，测量效率大大提高。若增大其单频率点的测量时间，能得到质量更好的频率特性曲线。

4 结论

本文提出了一种针对压阻检测的微机械谐振器的频率特性快速测试方法，其样机的等效输入噪声指标噪声有效值约为 2 ．7 nV/，单频率点测量时间为4 ms。而商用LIA:PerkinElmer 7265的输入等效噪声指标为 5 nV/，单频率点的测量时间为100 ms。微机械谐振器快速检测方法样机与PerkinElmer 7265相比，不但减小了等效输入噪声指标，而且大大缩短了单频率点的测量时间，提高了系统的测量效率，对压阻检测的微机械谐振器的检测方法研究有指导意义。

［1］ 樊尚春．传感器技术及应用［M］．北京:北京航空航天大学出版社，2004:206－241．

［2］ 陈德勇，崔大付，王利，等．微结构谐振梁式压力传感器研究［J］．传感技术学报，2000，13(4):255－259．

［3］ Greenwood J C．Etched Silicon Vibrating Sensor［J］．Journal of physics E:Scientific Instruments，1984，17(8):650－652．

［4］ Guckel H，Sniegowski J J，Christenson T R，et al．The Application of Fine-Grained，Tensile Polysilicon to Mechanically Resonant Transducers［J］．Sensors and Actuators A，1990，21(1－3):346－351．

［5］ 赵全斌，焦继伟，杨恒，等．基于压阻检测的双端固支硅纳米梁谐振特性研究［J］．传感技术学报，2006，19(5):1705－1708．

［6］ 高晋占．微弱信号检测［M］．北京，清华大学出版社，2004:17－257．

［7］ Sonnaillon M O，Urteaga R，Bonetto F J．High-Frequency Digital Lock-In Amplifier Using Random Sampling［J］．IEEE Transactions on Instrumentation and Measurement，2008;57(3):616－621．

［8］ Hu A，Vamsy P．CMOS Optoelectronic Lock-In Amplifier With Integrated Phototransistor Array［J］．IEEE Transactions on Biomedical Circuits and Systems，2010，4(5):274－280．

［9］ Davies R，Meuli G．Development of a Digital Lock-In Amplifier for Open-Path Light Scattering Measurement［C］//IEEE Symposium on Industrial Electronics and Application，2010:50－55．

［10］ Patel A，Kosko B．Noise Benefits in Quantizer-Array Correlation Detection and Watermark Decoding［J］．IEEE Transactions on Signal Processing，2011;59(2)488－500．

［11］ Lin I S，Weiner A M．Selective Correlation Detection of Photonically Generated Ultrawideband RF Signals［J］．Journal of Lightwave Technology，2008;26(15):2692－2699．

［12］邢维巍．硅谐振式传感器频率特性测试系统的研制［D］．北京:北京航空航天大学，1999:14－26．

［13］蔡晨光．硅微机械谐振式压力传感器闭环的研究与实现［D］．北京:北京航空航天大学，2007:28－85．

［14］樊尚春，杨军，肖志敏．硅谐振式微传感器开环特性测试与数据处理［J］．宇航学报，2006，27(5):1102－1106．

［15］王莹莹，樊尚春，邢维巍，等．硅谐振式压力微传感器模型与开环特性测试［J］．传感技术学报，2007，20(2):283－286．

［16］ PerkinElmer公司．Model7256 LIA 用户手册［S］．