小学数学练习题设计原则初探

　　目前，小学数学课堂教学重视凸显解决问题的教学过程与教学策略的研究，而忽视练习题设计的探讨，常出现“脚踏西瓜皮，练到哪里算哪里”的现象，严重阻碍了学生思维的发展和创新能力的培养。《数学课程标准》在“评价建议”中指出：“评价既要关注学生数学学习的结果，更要关注他们在学习过程中的变化和发展。”因此，加强教学流程中练习题设计研究显得至关重要。下面，笔者提出小学数学练习题设计的几条原则与大家一起交流探讨。
　　
　　一、思想性原则
　　
　　数学思维能力、情感态度和价值观，实际上就是数学教育中的德育问题。课堂练习实施思想性原则正是落实“三维”目标（情感、态度与价值观）的重要体现。教师除竭力挖掘教材中图文并茂的教学情境（主题图）外，还应主动挖掘教材中练习题的教育因素，寓思想教育于练习之中，做到“解题技能与思想教育”并举。如教学人教版五年级上册《解简易方程》时，为了训练学生列方程和解方程的技能，设计了一道练习题：一头猪重160千克，是一只猴子的10倍，这只猴子重多少千克？学生通过对题目的分析，很快找到等量关系，并列方程求得：这只猴子体重16千克。学生还借助图文应用题的情境图加以直观验证。这样，设计练习题让学生训练，严重缺乏思想教育内容，甚至那种“懒猪胖乎乎，老猴瘦巴巴”的形象在学生脑海里是根深蒂固的。为了起到“一箭双雕”的作用，可以这样设计练习题：⑴每平方米阔叶林每天能制造75克氧气，是每平方米草地每天制造氧气的5倍，每平方米草地每天能制造多少克氧气？⑵京广中心大厦是北京市目前最高的摩天大楼，它比中央电视塔矮196米。京广中心大厦高209米，中央电视塔高多少米？通过这组题目的训练，学生解题方法得到掌握、技能得到提高。同时，那种“种草地好，植树造林更好” “京广中心大厦高，中央电视塔更高”的形象在运算过程中得到渗透，从而进行了保护大自然环境、热爱新生活的思想教育。久而久之，学生的民族自尊心和凝聚力等思想教育就会得到很好的培养和锻炼。
　　
　　二、实效性原则
　　
　　所谓实效性练习题是指运用知识解决生活中的实际问题，并能激活与引领数学思考产生最大效益的习题。课堂练习实施实效性原则是优化课堂教学的重要举措，也是培养创新型人才的重要途径。因此，教师在练习设计上要重视现实素材的选择与加工，精心设计出既能考查学生知识与技能的掌握，又能考查学生运用知识灵活解决实际问题的能力的练习题。如教学人教版四年级上册《垂直与平行》时，为了训练学生画垂直与平行图形的技能，设计了一道练习题：过直线外一点，分别画已知直线L的垂线与平行线或画一个长3厘米、宽2厘米的长方形。显然，这样的练习题让学生训练只是“纸上谈兵”的机械训练，缺乏运用知识解决实际问题的训练，甚至阻碍了学生的思维发展。为了起到“一举两得”的效果，可以这样设计练习题：请画出从幸福村铺一条通往污水渠最短管道的示意图。学生在操作之前，要作出思维判断与选择：若是铺一条与污水渠平行的管道，则管道长度无法确定；若是铺一条与污水渠相交但不垂直的管道，则管道长或短可以选择；若是铺一条与污水渠相交且垂直的管道，则管道长度最短。又如教学人教版三年级上册《长方形的周长》时，可以这样设计练习题：新新小区要在一块长5米、宽3米的长方形花圃四周围上篱笆，篱笆长多少米？如果长方形的一条长边（或宽边）靠墙，篱笆长多少米？教学人教版六年级上册《圆的周长》时，可以这样设计练习题：公园里有一个周长为50.24米的圆形花圃，要在离花圃1米处围上一圈栅栏，栅栏长多少米？显然，这样设计练习题比设计用几何图形求周长的练习题，对深挖细掘思维有很好的效益。
　　
　　三、灵活性原则
　　
　　心理学家研究表明：如果一个人对某一活动有浓厚的兴趣，那么活动效率就高，而且不易产生疲劳和负担过重的感觉。因此，教师应精心设计灵活多变的习题，不断激发学生的思维。练习题设计体现灵活性原则主要表现：解题策略多样性（答案唯一型）和解题答案多样性（答案不唯一型）。
　　1.解题策略多样性
　　如教学人教版六年级上册《分数乘除法的应用题》时，为了训练学生用算术方法解答分数乘除法混合运算的技能，设计了一道练习题：养鸡场有母鸡500只，公鸡只数是母鸡的7/25，是小鸡只数的1/9。养鸡场有小鸡多少只？通过这种题型的训练，既能对学生进行判断单位“1”的量、找出“量与率”的对应关系和确定算法的训练，又能对学生进行分析推理能力的培养。但是，这种“单向”思维的习题，严重缺乏思维拓展内容，不利于开发运用多种途径解决问题的策略及培养创新思维能力。为了突出习题“多效价值”，让学生解题思维“活”起来，可以这样设计练习题：一台织布机1/9小时织5/4米布，照这样的速度，织9/16米布需要多少小时？此题的解题策略有：（1）1/9÷5/4×9/16=1/20（小时）；（2）9/16÷（5/4÷1/9）=1/20（小时）；（3）1/9×（9/16÷5/4）=1/20（小时）；（4）1/9÷（5/4÷9/16）=1/20（小时）。显然，常设计这种题型让学生训练，能启发与引领学生思维多向性、灵活性，并养成多角度解决问题的习惯。
　　2.解题答案多样性
　　如教学人教版六年级上册《稍复杂分数的应用题》时，为了训练学生综合运用知识解决实际问题的技能，设计一道练习题：一套家具原价3200元，现价比原价多1/5。现价多少元？学生通过对关键句的数量分析，结合线段图，很快找到解题策略：求现价就是求原价的（1+1/5）是多少？列式：3200×（1+1/5）。这种“单列”思维的习题，严重缺乏思维对比内容，不利思维辨别能力的训练，容易产生解题思维错误现象。为了突出习题“高效功能”，让学生解题思维“动”起来，可以这样设计练习题：一套家具原价3200元，__________。现价多少元？[①现价比原价多1/5；②现价比原价少1/5；③原价比现价少1/5；④原价比现价少1/5；⑤现价是原价的1/5；⑥原价是现价的1/5。]（依次把条件填在横线上并解答，或选择一个你喜欢的条件填在横线上并解答。）显然，常设计这种题型让学生训练，既能激发学生强烈的探究欲望，又能提高解题技能。
　　
　　四、趣味性原则
　　
　　儿童的心理特点是好奇、好动、好玩。由于受应试教育的影响，数学课堂仍然出现机械重复、枯燥乏味、死记硬背的现象，使学生对数学学习产生厌烦情绪，严重阻碍了学生的发展。因此，练习题设计不仅要从新的形式、新的题型、新的要求出发，还要力求“问题解决”的趣味性。如教学人教版五年级上册《平行四边形的面积》时，为了训练学生运用公式解决实际问题的能力，设计了一道练习题：把一个长18厘米、宽15厘米的长方形木条框架，拉成一个平行四边形，周长和面积与原来相比各发生了怎样的变化？学生通过画图想象、学具操作等手段，探索出周长与原图形相比相等、面积与原图形相比变小的规律，且长与宽的夹角越小面积就越小。这种从“静态到动态”的习题设计，利于激发学生探索思维，但还严重缺乏趣味性内容。为了突出习题“有效作用”，让学生解题思维“乐”起来，可以这样设计练习题：很早以前，有一位财主对阿凡提很苛刻，想整死他。于是，就派佣人用篱笆在一片宽阔的田地上围成一块长18米、宽15米的长方形菜地，并要求阿凡提在一天时间内按翻地标准把这块菜地翻一遍，且围成菜地的篱笆长度1米也不能短。否则，不给阿凡提吃、住，甚至要扣下前面打工的所有工资。聪明的阿凡提想出了一个很好的办法，既做到按质完成翻地任务，又做到使财主无可奈何。谁来猜一猜阿凡提想出了一个什么样的办法？并说明理由。显然，对这种有趣味性的习题，学生解题时兴趣盎然。又如教学人教版六年级上册《圆的面积》时，设计了一道趣味题：以前，有一个财主想敲诈一位雇工的工资，拿了一块大羊皮给雇工到海边占地作为工资。谁能想出好办法替这位雇佣到海边占地呢？显然，剪成细羊皮条圈地比用整块羊皮占地面积大。如果剪成羊皮条的长度是25.12米，那么该怎么样圈地面积才会最大？有的学生说：圈成一个圆；有的学生说：一边靠海，圈成一个半圆。学生通过计算，悟出了圈成一个半圆比圈成一个圆面积大的道理。
　　
　　五、层次性原则
　　
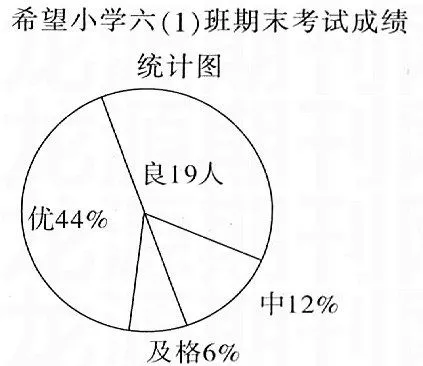
　　练习题设计既要关注学困生，又要重视中等生，还要兼顾优等生。因此，设计层次性题型让学生选择训练是激活不同层次学生解题思维的重要策略。如教学《长方体和正方体的表面积》时，可以这样设计一道练习题：有一个正方体，棱长总和为48分米。请你选择一个或几个问题解答。问题：① 这个正方体的表面积和体积各是多少?②如果把这个正方体切成两个完全相同的小长方体，表面积会增加多少平方厘米?③把这个正方体从上到下挖出一个长方体孔洞，孔洞的底边为边长2厘米的正方形，求空心图形的表面积和体积各是多少？又如教学《统计图》时，可以这样设计一道练习题:看图作答。
　　设计了两道基本题：①六（1）班共有学生（ ）人？②得良的同学占全班同学人数的（）%。设计一道选做题：提出一个自己喜欢的问题并解答。这样，学困生可提一步计算的问题，如得优的有多少人?中等生可提二步计算的问题，如得优与良的共有多少人？优等生可提三步计算的问题，如得优、得良与得中的共有多少人?
　　这样，通过层次性习题的思维训练，既能充分调动学生解题思维的积极性，又能让不同层次的学生有不同的受益与发展。
　　总之，在教学中，要取得有效的练习效果，让数学练习题发挥最大的效益，就要在练习设计上多动脑筋，精心设计练习题，力求做到课堂的练习数量适当、难易适中、形式多样，从而有效地优化数学教学。