浅谈如何使用法向量求解立体几何中的角与距离

凌启圣

（合肥市第一中学 数学组，安徽 合肥 230061）

浅谈如何使用法向量求解立体几何中的角与距离

凌启圣

（合肥市第一中学 数学组，安徽 合肥 230061）

中学数学现行人教版教材在引入空间向量后，原本较为复杂的几何问题得到了不少简化，特别是向量几何中的一个重要的工具——法向量引入，使得许多原本复杂难解的问题变得简单易解。通过日常教学中接触到的例子，对使用法向量求解立体几何中夹角与距离的问题进行归纳和总结。

法向量；立体几何；夹角与距离；中学数学；高考

在很多学生的眼里，数学是非常难的。美国教育家戴维斯教授曾指出，一些学生正是由于数学学习失败而丧失了对于整个人生的信心。随着素质教育的推行，精英教育逐步走向大众教育，更多的学生面临数学学不好特别是几何学不好的难题。在传统几何中，辅助线的添加更多来自于灵感闪现，解题中对空间想象能力和逻辑推理能力的要求极高，几何特别是立体几何令人望而生畏。中科院院士、著名数学家张景中教授一直在疾呼改造数学教育特别是几何教育，把数学变得容易些[1]。在这样的背景下，向量走进了中学数学课堂，向量法解题得到了空前重视。向量法解题以计算代替演绎，有效地降低了解题难度。

传统的立体几何夹角与距离的求解过程对作图能力、空间想像能力、逻辑推理能力要求都很高，解题过程非常繁琐，学生经过大量训练却仍然不得要领，严重挫伤他们的学习积极性。而引进坐标系、使用法向量，将会使这些问题变得简单易解，学生很快就能掌握要领。下面对法向量的应用作简单归纳与总结。

一、利用法向量求点到平面的距离

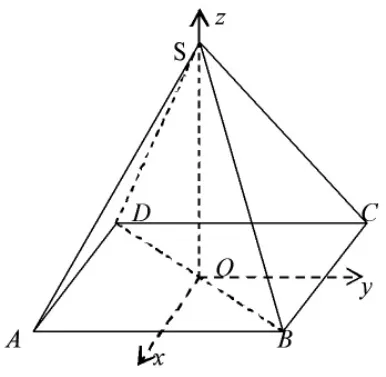
例1：（2010年江西高考理科数学试题）如图△BCD与△MCD都是边长为2的正三角形，平面MCD⊥平面 BCD，AB⊥平面 BCD，AB=2。 求点A到平面MBC的距离。

分析：取 CD 中点 O，连 OB，OM，则 OB⊥CD，OM⊥CD，又平面MCD⊥平面BCD，则MO⊥平面BCD，以 O 为原点，直线 OC、BO、OM 为 x轴，y轴，z轴，建立空间直角坐标系如图。

二、利用法向量求两条异面直线间的距离

三、利用法向量求线面所成角

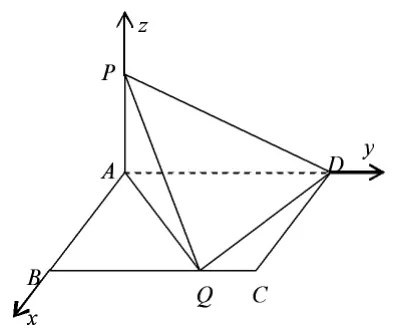
例3：在矩形 ABCD中，已知 AB=1，BQ=2QC=1，PA⊥平面ABCD，且PA=1，求AD与平面PDQ所成角的正弦值。

四、利用法向量求面面所成角

例4：（2009年山东高考理科试题）如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为等腰梯形，AB//CD，AB=4，BC=CD=2，AA1=2，E、E1、F 分别是棱 AD、AA1、AB 的中点。

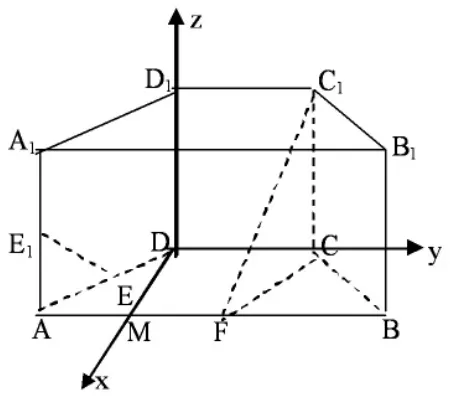
（1）证明：直线 EE1//平面 FCC1；

（2）求二面角B-FC1-C的余弦值。

在例4第（1）题中，我们还使用法向量证明了线面平行，即证明直线与平面的法向量垂直。类似的，我们还可以使用法向量证明面面平行（垂直），即只需证两平面的法向量共线（垂直），但这些类型的题直接利用传统方法也比较容易解答，故在此不加赘述。

法向量引入后降低了对空间想像能力与几何作图能力的要求，简化了解题思路与解题运算，将复杂的几何问题转化为了代数运算。空间向量为处理立体几何问题提供了新的视角，空间向量的引入，为解决三维空间中的位置关系和度量关系提供了一个十分有效的工具[2]。当然，过分依赖向量方法解决几何问题是不当的，我们在教学中也应该注意：不能过分强调向量的机械化运算而忽视对几何元素的分析，只见代数不见几何。“去几何化”倾向是应该避免的[3]。在教学中，应该鼓励学生灵活选用向量方法和综合方法，从不同的角度解决立体几何问题。

[1]张景中，彭翕成.绕来绕去的向量法[M].北京：科学出版社，2010

[2]严士健，张奠宙，王尚志.普通高中数学课程标准（实验）解读[M].南京：江苏教育出版社，2004

[3]李善佳.高中向量法解题的现状与研究[D].天津：天津师范大学，2009

G633.6

A

1009-9530（2011）05-0130-03

2011-07-23

凌启圣（1980-），男，安徽潜山人，合肥市第一中学教师。