高斯整数环的素元形成与商环性质

戴洋

（山东大学 数学学院，山东 济南 250100）

高斯整数环的素元形成与商环性质

戴洋

（山东大学 数学学院，山东 济南 250100）

高斯整数环是一种构造特殊且具有一定代表性的环，在代数环论中占有重要的地位。既融入了环论的思想，同时亦包含有数论的思想，对于高斯整数环的研究一直是国内外学者的重要课题之一，数学家们通过多年的研究，得出了许多重要且富有意义的结论。在前人研究成果的基础上，针对高斯整数环中素元的形成和不同主理想下商环的个数，作了进一步的探索：

1、分析证明了高斯整数环的基本性质，论证了高斯整数环是欧几里德整环，高斯整数环是主理想整环，高斯整数环是唯一因式分解整环。

2、论述了高斯整数环素元的形成，分别给出了整数素元和部分非整数素元的形式。

3、论述了高斯整数环在不同主理想下其商环的个数。对于高斯整数环的主理想，分别给出了当（为自然数），（为自然数），（为任意整数）时，其商环的个数及其证明。

高斯整数环；素元；商环

1 高斯整数环的基本性质

1.1 高斯整数环是欧几里德整环

定理1.1.1高斯整数环是欧几里德整环。

证明：高斯整数环 Z[i]，设 α∈Z[i]，有

1.2 高斯整数环是主理想整环

定理1.2.1欧几里德整环是主理想整环。

证明：设R是欧几里德整环。任取R的一个理想I且设I≠0。取I的一个非零元b，使得

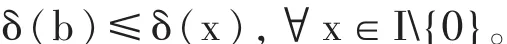
显然（b）⊆I。 反之，设 a∈I，由于 R 是欧几里德整环，因此存在 h，r∈R，使得

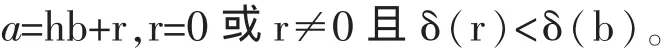
当r≠0时，则r=a-hb∈I，这与b的取法矛盾。因此 r=0，从而 a=hb∈（b）。 因此 I=（b）。 证毕。

定理1.2.2高斯整数环是主理想整环。

证明：由定理1.1.1和定理1.2.1可知，高斯整数环是主理想整环。证毕。

1.3 高斯整数环是唯一因式分解整环

定理1.3.1整环R如果满足下列两个条件：

（i）因子链条件成立，即如果序列 a1，a2，a3，…中，每一个ai是ai-1的真因子，则这个序列是有限序列；

（ii）每一个不可约元都是素元，则R是唯一因式分解整环。

证明：设a是R中非零且非单位的一个元素。如果a不可约，则a=a。下面设a可约，则a有真因子。先证a有一个真因子是不可约的。设a1是a的一个真因子。若a1不可约，则a1就是所要找的。若a1可约，则a1有真因子a2。若a2不可约，则a2有真因子a3。如此下去，得到序列

其中每个元素是前面一个的真因子。由于R满足因子链条件，因此（1）是有限序列。设它的最后一项为an。则an是不可约的。易看出an是a的真因子，把 an记作p1，于是a=p1c1。 从而 c1是 a的真因子。若c1不可约，则a分解成了两个不可约元p和c1的乘积。若c1可约，显然c1非零且非单位，由前面的讨论知道，c1有真因子p2不可约，于是c1=p2c2，从而c2是c1的真因子。如此下去，得到序列

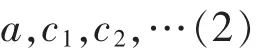
其中每一个元素是前面一个得真因子，由因子链条件，序列（2）有限。 设序列（2）终止于 cs-1。 于是cs-1为ps，则

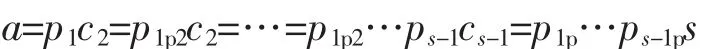
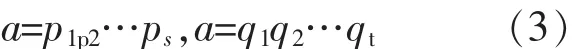
再证唯一性，设a有两种这样的分解：对第一种分解式中的不可约元的个数s作数学归纳法。

s=1 时，a=p1=q1q2…qt。 假如 t＞1，则

因为p1不可约，所以q1是p1的平凡因子，由于q1不是单位，因此q1~p1。于是q1=p1u，其中u为单位。从而

由此推出，1=u （q2…qt）。 从而 q2是单位 i，矛盾。因此t=1。于是p1=q1。

假设分解式中不可约元的个数为s-1时唯一性成立，讨论不可约元的个数为s的情形。

由于 p1不可约，根据已知条件（ii）得，p1为素元。于是从p1|q1q2…qt可推出p1整除某个qi。通过改写的qi下标可设p1|q1。由于q1不可约，因此p1~q1。于是p1=q1v，其中v是单位。从而

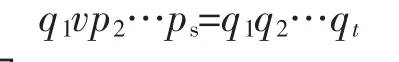
两边消去 q1，得（vp2）……ps=q1q2……qt。 由归纳假设得，s-1=t-1，即s=t；并且适当改写qj的下标可以使 vp2~q2，p3~q3，…，ps~qs，从而有

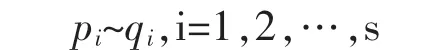
根据数学归纳法原理，唯一性得证。

综上所述，R为唯一因式分解整环。证毕。

定理1.3.2主理想整环是唯一因式分解整环。

证明：设R为主理想整环，设p为R的一个不可约元，则p≠0且p非单位，（p）是p生成的理想。于是（p）≠0 且（p）≠R。设 R 的理想 I⊇（p），因为 R 是主理想整环，所以 I=（a）。 从（a）⊇（p）得出a|p。由于p只是平凡的因子，因此a~p或a是单位。如果 a~p，则（a）=（p）。如果 a 是单位，则（a）=R。因此（p）是R的极大理想。

因为（p）是非零极大理想，从而（p）是非零素理想，因此p是素元。

R 中任取一个序列 a1，a2，a3，…，其中每个 ai是ai-1的真因子。 于是（ai）■（ai-1）。 从而

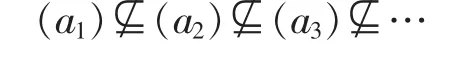
综上所述，R是唯一因式分解整环。证毕。

2 高斯整数环中素元的形成

2.1 Z[i]中的单位

定理2.1.1 Z[i]中的单位只有±1，±i四个元素。

证明：设 α，β∈Z[i]其中 α=a+bi，由题意知αβ=1，有 φ（αβ）=φ（α）φ（β）=1。 由于 φ（α）、φ（β）是非负整数，因此只有 φ（α）=φ（β）=1，即有 φ（α）=a2+b2=1。 由上式得 a=0，b=±1，α=±i或 a=±1，b=0，α=±1，即Z[i]中的单位只有±1和±i四个元素。证毕。

2.2 Z[i]中的素元当且仅当是不可约元

定理2.2.1 Z[i]中的素元当且仅当是不可约元。

证明：充分性：设α为Z[i]中的不可约元，并有 α|βγ（β，γ∈Z[i]），由定理 1.1.1 和定理 1.2.2 可知：

令 α=ε1δ，β=ε2δ，ε1ε2∈Z[i]。 因为 α 是 Z[i]的不可约元，故ε1、δ中必有一个是单位。若ε1是单位，则 δ=ε1-1α，β=（ε2ε1-1）α 即 α|β；若 δ 是单位，由（δ）=（α，β），故可设δ=ε3α+ε4β，ε3，ε4∈Z[i]。于是 1=δ-1ε2α+δ-1ε4β，则 γ=δ-1ε2αγ+δ-1ε4βγ，由于 α|βγ 及 α|αγ 故α|γ，因此α为Z[i]中的素元。充分性得证。

必要性：设 α是 Z[i]中的素元，若 α=βγ，则有α|β 或 α|γ，不妨设 α|β，可设 β=εα ε∈Z[i]，故 α=βγ=（εγ）α，由于 Z[i]是无零因子环，所以有 εγ=1，即得γ是单位，故α是不可约元。必要性得证。

2.3 Z[i]中的整数素元

对于环Z[i]，它的元素可分为两部分，一部分是整数，另一部分是形如 a+bi（b≠0）的元素。首先讨论整数集Z中的素元。Z中的非素数肯定不是Z[i]中的素元，因为Z[i]中的素元要求除本身及单位外无其他因子，故只有素数才可能是Z[i]中的素元。但并非Z中的一切素数都是Z[i]中的素元，例如素数 2 在 Z[i]中可分解为 2=（1+i）（1-i），1±i都不是2的相伴元，显然它不是Z[i]中的素元。一般的，除2外，其他素数都可以写成4n+1与4n+3的形式，有如下定理：

定理2.3.1有理素数p为Z[i]中素元的充分必要条件是方程x2+y2=p没有整数解。

证明：必要性：设p为素元，假设x2+y2=p有整数解（x0，y0），则有 p=（x0+y0i）（x0-y0i），且 x0，y0≠0，即p有真因子x0±y0i，与p为素元矛盾，故假设错误，即 p 为素元，x2+y2=p 没有整数解（x0，y0）。 必要性得证。

充分性：设 x2+y2=p 没有整数解（x0，y0），假设 p不是素元，即 p 可分解。 设 p=（a+bi）（c+di），且 φ（a+bi）≠1，φ（c+di）≠1，则

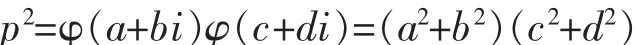
从而a2+b2|p2或c2+d2|p2， 即p2+b2=p2或c2+d2=p2。 由 c2+d2≠1 知，a2+b2=p。 又由 a，b∈Z 知，x2+y2=p有整数解（a，b），与假设矛盾。故假设错误，即p为Z[i]中的素元。充分性得证。

定理2.3.2若素数p可写成4n+3的形式，则p为Z[i]的素元。

证明：由定理2.3.1，只需证4n+3=x2+y2无整数解即可。

由于k12+k22只能为 0、1和2，而不可能为 3，故上式不可能成立。即p=4n+3类的素数为Z[i]的素元。证毕。

定理2.3.3形为4n+1类的素数为Z[i]的非素元。

证明：由数论知，若p=4n+1为素数，则-1为p的平方剩余，即 x2≡-1（modp）有解，所以存在 a∈Z，使得 p|a2+1。

若 p 为素元，由 p|a2+1=（a+i）（a-i），则有 p|（a+i）或 p|（a-i）。 不妨设 p|（a+i），即（a+i）=p（c+di），这里c，d∈Z，所以1=pd，而这与p=4n+1为素数矛盾。故p为Z[i]的非素元。证毕。

2.4 Z[i]中的非整数素元

定理 2.4.1 设 α∈Z[i]，若 φ（α）为素数，则 α 为Z[i]中的素元。

证明：设 p 为素数，φ（α）=p，x为 α 的任意因子，设 α=xy，则有 φ（α）=p=φ（x）φ（y），因此 φ（x）=1或 φ（x）=p。

（1）若 φ（x）=1，则 x为一单位，故 x为 α 的平凡因子；

（2）若 φ（x）=p，则 x为 α 相伴元，故 x为 α 的平凡因子；

因此，α的任意因子必为α的平凡因子，故α为Z[i]中的素元。证毕。

定理 2.4.2 若 α∈Z[i]，α∉Z，φ（α）=p1p2…pn，pi为素数，则

（1）若 n=1，则 α 为 Z[i]中的素元；

（2）若 n＞1，则 α 为 Z[i]中的非素元。

证明：（1）由定理 2.4.1所证。

（2）设 α=a+bi，a，b∈Z，b≠0，则 φ（α）=（a+bi）（a-bi）=p1p2…pn。 若 pi（i=1，2，…n）中存在 2 或 4n+1类的素数，不妨设p2即是，则

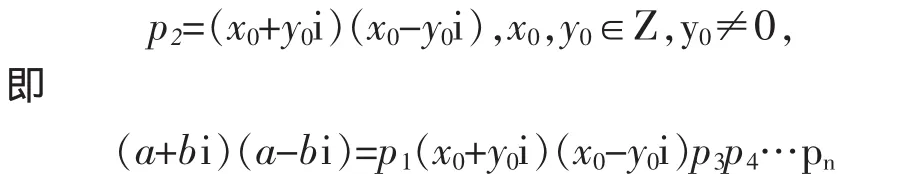
由定理1.3.1知Z[i]是唯一因式分解整环，故a+bi要么为x0+y0i，要么还可继续分解。而由p1为素数可知a+bi不可能为x0+y0i，故此时α为Z[i]的非素元。若p1p2…pn全为4n+3形式的素数，那么p1p2…pn即为φ（α）的一个分解。由唯一分解性，a+bi仍可继续分解，显然其不是素元。证毕。

3 高斯整数环的商环的性质

由文[3]的讨论，我们只需考虑mn≠0的情形，

[1]丘维生.抽象代数基础[M].北京：高等教育出版社，2003

[2]石生明.近世代数初步[M].北京：高等教育出版社，2002

[3]王萼芳，石生明.高等代数[M].北京：高等教育出版社，2003

[4]王海坤.Gauss整数环的诸类问题探[J].工科数学，1999，（15）：3

[5]方辉.高斯整数环及其商环的若干性质[J].安徽教育学院学报，2002，（20）：6

[6]齐丽丽.Gauss整数环及其商环的几个性质[J].贵州大学学报（自然科学版），2008，（30）：1

O153.3

A

1009-9530（2011）05-0017-04

2011-07-12

戴洋（1989-），男，安徽合肥人，山东大学数学学院数学与应用数学专业学生。