一种基于正区域及其分类纯度的决策树算法

蒋慧平 费耀平

(1.中南大学信息科学与工程学院，湖南长沙 410012;2.湖南广播电视大学，湖南长沙 410004;3.中南大学现代教育技术中心，湖南长沙 410012)

一种基于正区域及其分类纯度的决策树算法

蒋慧平1，2费耀平3＊

(1.中南大学信息科学与工程学院，湖南长沙 410012;2.湖南广播电视大学，湖南长沙 410004;3.中南大学现代教育技术中心，湖南长沙 410012)

本文分析了基于正区域的决策树生成算法的不足，针对这些不足，提出了基于正区域及其分类纯度的决策树算法。该方法计算简单，易于理解，并用实例说明了该方法的优越性。

粗糙集;决策树;正区域;分类纯度

一、引言

决策树是以实例为基础的归纳推理学习算法，它从一组无序、无规则的元组中推导出分类规则，具有高效、直观的特点。决策树算法的关键是属性选取标准，作为决策树的经典算法ID3能较好地提高分类速度和准确率，但该算法仍存在许多不足。为此，一些学者将粗糙集理论［1］［4］引入决策树，纷纷提出基于粗糙集理论的决策树算法［1］［5］［6］［7］:用粗糙边界［4］的大小作为属性选择标准或以正区域作为属性标准［5］，但实际上，粗糙边界最小的属性会有多个，得到的决策树的泛化能力不好［7］。

针对上述不足，本文基于粗糙集理论和决策树算法的基本原理，提出了一种改进算法:基于正区域及其分类纯度的决策树算法，提高了决策树对于未知样本的分类和预测能力。最后的实例表明，本文方法正确有效，简单实用，明显优于传统的 ID3算法。

二、粗造集基本概念

定义1 决策系统

一个决策系统是一个有序四元组:S=(U，A，V，f)，其中 U 是论域，U={X1，X2，…，Xm}，A=C∪D，其中C是条件属性集，D是决策属性集;V=∪{Va:a∈A}是属性值的集合，Va是属性a的值域;f:U×A→V是一个信息函数，对每一个a∈A和x∈U，定义一个信息函数f(x，a)∈Va，即信息函数f指定U中的每一个对象x的属性值。当属性集合A不划分为条件属性子集合和决策属性子集合时，该系统又称为信息系统［9］。

定义2 上近似、下近似、边界和R-正区域

对信息系统S=(U，A，V，f)，设R⊆A，X⊆U，则IND(R)是U×U上的等价关系，R(xi)是按等价关系IND(R)得到的包含xi的等价类，称R(xi)为R基本集。用属性B对U进行划分，获得的是一个等价类集。子集X的下近似R*(X)和上近似R*(X)分别定义为:R*(X)={x∈∪|［x］R⊆X}，R*(X)={x∈∪|［x］R∩X≠Φ}，BNR(X)=R*(X)-R*(X)为X的边界。POSR(X)=R*(X)称为集合X 的 R- 正区域［10］。

三、相关工作分析

用正区域作为属性标准的方法，存在着相同的属性较多、不易选择属性和叶子结点的泛化能力不足的问题。以下面的例子为例:

例1:U={b1，b2，b3，b4，b5，b6，b7，b8，b9}，A，Y，Q是条件属性，D是决策属性。

U/D={(b1，b2，b3，b4，b5，b6)，(b7，b8，b9)};U/A={(b1，b2)，(b3，b4，b5)，(b7，b8)，(b6，b9)};U/Y={(b1，b2，b3，b4)，(b5，b7，b8)，(b6，b9)};U/Q={b1，b2，b3，b4，b5，(b7，b8)，(b6，b9)}.

由正区域定义可以|POSA(D)|=7，|POSY(D)|=7，|POSQ(D)|=4。按基于正区域的属性选择标准应该选择属性A或者Q。但实际上选择属性A最为合理，因为由A分割出来的决策树的叶子结点最小，且得到的决策树的叶子深度最小。

理想的决策树的要求是:叶子结点最少，叶子结点深度最小，叶子结点最少且结点深度最小［7］。为解决上述问题，本文根据正区域区分能力的思路，先定义条件属性正区域的分类纯度［8］。

定义3 决策表T=(U，C，D)，u为论域，A⊆C，U/D={Y1，Y2，…，Ym}，U/A={Al，A2，…，An}，记A的正区域为POSA(D)={P1，P2，…，Pk}，则该条件属性正区域的分类纯度［8］定义为:

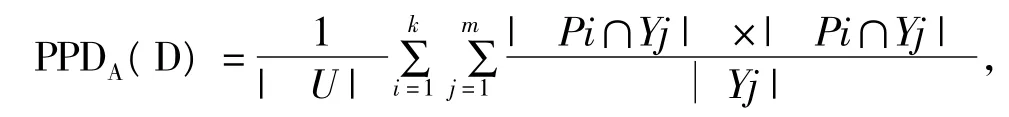
显然0＜PPDA(D)≤1。

条件属性正区域的分类纯度反映了对决策属性的分类程度，值越高，反映分类能力越强。

对于例1，可得:

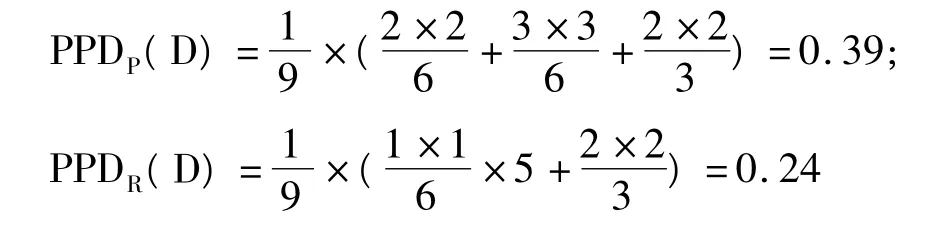
可见，选择属性P作为分类属性是合理的。

例2:U={a1，a2，a3，a4，a5，a6，a7，a8，a9}，P，Q，R是条件属性，Y是决策属性。U/Y={(a1，a2，a3，a4，a5，a6)，(a7，a8)，a9};U/P={(a1，a2)，(a3，a4，a5)，(a6，a7，a8，a9)};U/Q={(a1，a2，a3)，(a7，a8)，(a4，a5，a6，a9)};U/R={a1，a2，a3，a4，(a5，a6，a7，a8)，a9}。

由正区域定义可知:

|POSP(Y)|=|POSQ(Y)|=|POSR(Y)|=5，PPDP(D)=0.24，PPDQ(D)=0.22，PPDR(D)=0.19。

|POSP(Y)|+PPDP(D)=5.24，为最大，故选择属性P最为分类属性是合理的。

四、算法

记POSPPD(D)=|POSA(D)|+PPDA(D)，该算法描述为:

输入:训练样本集U，条件属性C，决策属性D

输出:决策树

(1)创建结点;

(2)计算训练样本集U条件属性的POSPPD;

(3)从C中选择POSPPD(D)为最大的那个属性A作为测试属性;

(4)以A为根建立决策树;对A的可能取值进行计算，若没有到达叶子节点，则继续调用该算法;

(5)返回树。

五、实例

以下面的决策表来说明新算法。

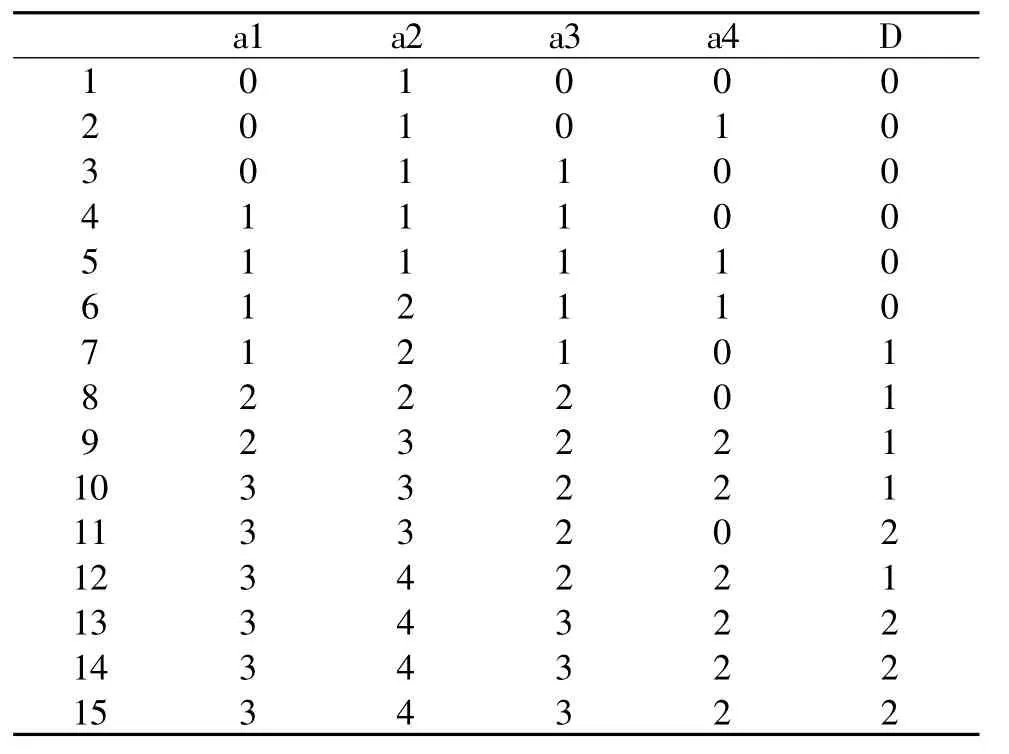
决策表

a1，a2，a3，a4 为条件属性，D 为决策属性。

U/a1={(1，2，3)，(4，5，6，7)，(8，9)，(10，11，12，13，14，15)};

U/a2={(1，2，3，4，5)，(6，7，8)，(9，10，11)，(12，13，14，15)};

U/a3={(1，2)，(3，4，5，6，7)，(8，9，10，11，12)，(13，14，15)};

U/a4={(1，3，4，7，8，11)，(2，5，6)，(9，10，12，13，14，15)}

U/D={(1，2，3，4，5，6)，(7，8，9，10，12)，(11，13，14，15)};

根据算法可得:

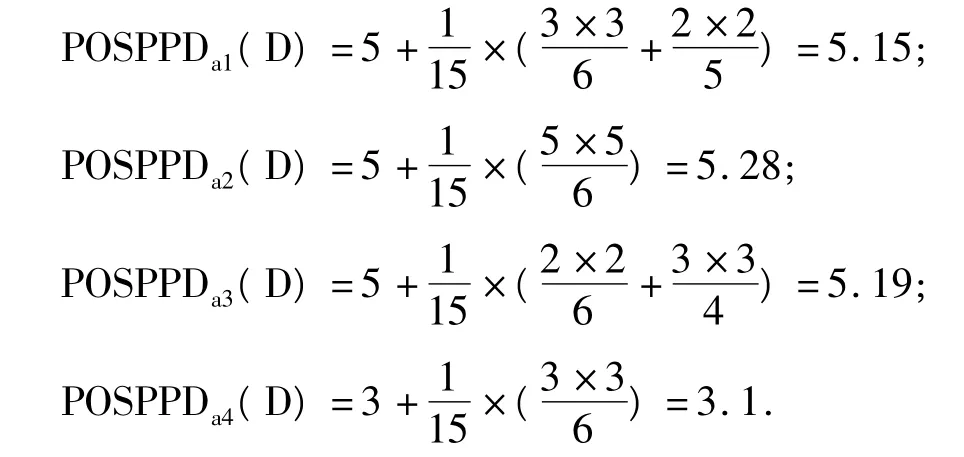
故选择属性a2。

对于数据集(6，7，8)，(9，10，11)，(12，13，14，15)，依照上述计算，选择相应的条件属性，最后得到决策树如图1所示:

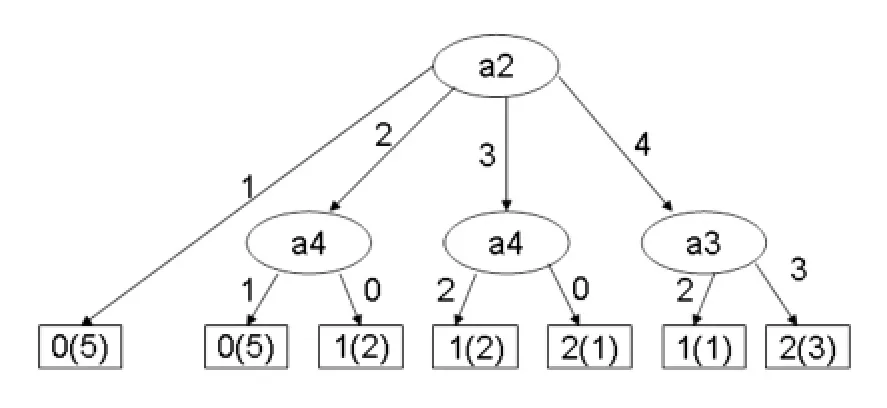
图1 新算法生成的决策树

相对于正区域的属性选择标准(分别选择属性a1，a2)，生成的决策树图2、图3，基于新算法生成的决策树更理想。

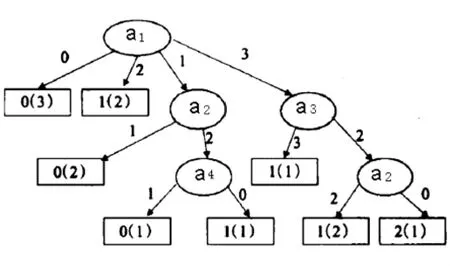
图2 基于正区域决策树算法(选择属性a1)

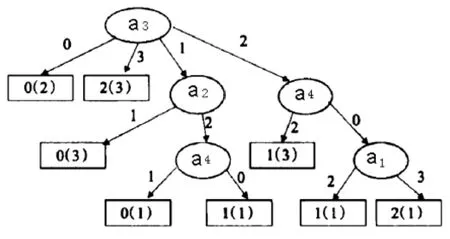
图3 基于正区域决策树算法(选择属性a3)

六、结论

本文提出了一种基于正区域及其分类纯度相结合的决策树算法，所生成的决策树叶子数目较小、叶子的平均深度较小，效率高，实例说明新算法提高了决策树的分类和预测能力。

［1］邹瑞芝，罗可，曾正良.基于粗糙集理论的决策树分类方法［J］.计算机工程与科学，2009，31(10):112-114.

［2］Quinlan J R.Simplifying decision trees［J］，International Journal of Man-Machine Studies，1987，27(3):221-234.

［3］王国胤.Rough集理论与知识获取［M］.西安:西安交通大学出版社，2001.

［4］张文修，吴伟志等.粗糙集理论与方法［M］.北京:科学出版社，2003.

［5］王名扬，卫金茂，尹卫国.基于粗造集理论的新决策树剪枝方法［J］.东北师范大学(自然科学版)，2005，37(3):28-32.

［6］朱红.基于Rough Set的最简决策树去顶算法的研究［J］.计算机工程与应用，2003，41(13):129-131.

［7］高静，杨炳儒，徐章艳，宋威.一种改进的基于正区域的决策树算法［J］.计算机科学，2008，35(5):138-142.

［8］乔梅.基于粗糙集和数据库技术的知识发现与推理方法研究［D］.天津大学，2005.

［9］蒋芸，李战怀，张强，刘杨.一种基于粗糙集构造决策树的新方法［J］.计算机应用，2004，(8).

［10］张玉红，胡学钢，郑锦良.基于粗糙集决策树优化研究［J］.合肥工业大学学报，2009，(12).

An Algorithm for Decision Tree Based on Positive Region and Its Classification Ability

JIANG Hui-ping，FEI Yao-ping

In this paper，disadvantages of algorithm for constructing decision tree based on positive region are analyzed.Aiming at these disadvantages，a new algorithm for decision tree based on positive region and its classification ability is proposed.The method is simple and easy-to-understand.The example shows that the method is effective.

rough sets;decision tree;positive region;classification ability

TP183

A

1009-5152(2011)03-0057-03

2011-07-25

蒋慧平(1972- )，男，湖南网络工程职业学院副教授。