第一类李拟代数的Frattini子代数与c可补子代数

温启军，肖玉山

（长春大学理学院，吉林长春 130022）

第一类李拟代数的Frattini子代数与c可补子代数

温启军，肖玉山

（长春大学理学院，吉林长春 130022）

把Frattini理论推广到第一类李拟代数，得到了第一类李拟代数的Frattini子代数的若干性质，并研究了第一类李拟代数的c可补子代数的重要性质，给出它们之间的重要关系.

第一类李拟代数；Frattini子代数；c可补子代数

1 预备知识

李代数不仅在数学领域中具有重要的地位，而且在理论物理研究中也具有不容忽视的作用.作为李代数（李超代数）的自然推广，人们给出6种新推广的代数，分别称为第一、二、三类李拟代数，根据结合代数与李代数之间的密切联系，文献［1］给出了不变子代数和第一、二、三类李拟代数（李拟超代数）之间的密切联系.

在文献［1］中，作者把有限维李代数对于基的结构常数、可解性、幂零性、同态基本定理、导子等性质推广到了在一个非空有限集合S上诱导出的第一类李拟代数上，主要给出了第一类李拟代数的相应性质［2－5］.李代数等代数的Frattini子代数与c可补子代数已经有了较多的研究［4－8］，本文主要把Frattini理论推广到第一类李拟代数，得到了第一类李拟代数的Frattini子代数的若干性质，研究了第一类李拟代数的c可补子代数的重要性质，并给出它们之间的重要关系.本文总设S是非空集合，符号和术语与文献［3－6］一致.

定义1.1［4］设G是域F上的线性空间，若G中有二元双线性运算（x，y）→［x，y］满足以下两个条件：

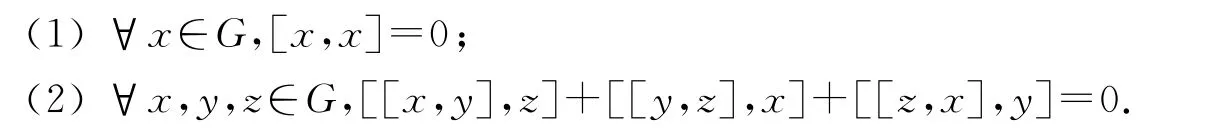
则称G为域F上的李代数.条件（2）称为Jacobi恒等式.

定义1.2［1］设L是域F上的向量空间，在L中定义了一个二元双线性运算集合｛［·，·］k｜k∈S｝，其中［·，·］k：L×L→L是一个二元映射，若以下两个条件成立：

则称L为在S上诱导出的第一类李拟代数，记为（L，［·，·］k∈S）.条件（2）称为Jacobi拟恒等式.

定义1.3［1］L为在S上诱导出的第一类李拟代数，I是L的子空间.若∀k∈S，有［L，I］k⊆I，则称I是L的理想.

定义1.4［1］L为在S上诱导出的第一类李拟代数，N是L的子空间.若∀k∈S，有［N，N］k⊆N，则称N是L的子代数.

定义1.5L为在S上诱导出的第一类李拟代数，D是L上的一个线性变换，如果∀k∈S，∀x，y∈L，D（［x，y］k）＝［Dx，y］k＋［x，Dy］k，则称D为L一个导子，记DerL＝｛D∈ɡl（L）｜D为L的导子｝.

例 设S为非空集合，V是复数域C上的n维向量空间.记V上的所有线性变换的集合为ɡl（V），由定义1.2知ɡl（V）关于方括号积｛［A，B］k＝φ（k）（AB－BA）｜A，B∈ɡl（V），k∈S｝构成在S上诱导出的第一类李拟代数，其中φ：k｜→φ（k）是一个从S到F＊的映射，那么李代数L可以被视为在S上诱导出的第一类李拟代数.

2 Frattini子代数

3 c可补第一类李拟代数

若x∉N（L），则存在L的理想C满足x∉C.故L／C是幂零的.

设x1∉N（L）与C1是满足x1∉C1的理想且L／C1是幂零的.若C1⊆N（T），则结论成立；若不是，则选取x2∈C1＼N（L），并设C2是满足x2∉C2的理想且L／C2幂零.显然

致谢 感谢陈良云副教授在我访问东北师范大学数学与统计学院时给予的指导与帮助！

［1］KWASNIEWSKI，ANDRZEJ KRZYSZTOF.On graded Lie－like algebras［J］.Bull Soc Sci Lett，1989，39：5－19.

［2］温启军，钱玲，陈良云.Jordan李代数的分解与Frattini理论［J］.东北师大学报：自然科学版，2010，42（4）：12－16.

［3］TOWER D A，VAREA V R.Elementary Lie algebras Lie algebras［J］.J Algebra，2007，312：891－901.

［4］STITZINGER E L.The Frattini subalgebra of a Lie algebras［J］.J London Math Soc，1970，2（2）：177－182.

［5］MALEK A A.The Frattini subalgebra of a malcev algebras［J］.Arch Math，1981，37：306－315.

［6］CHEN L Y，MENG D J，ZHANG Y Z.The Frattini subalgebra of restricted Lie Superalgebras［J］.Acta Math Sinica：English Series，2006，22（5）：1343－1356.

［7］BECHTELL H.Frattini subgroups andφ－central groups［J］.Pacific J Math，1966（18）：15－23.

［8］BAI R P，CHEN L Y，MENG D J.The Frattini subalgebra ofn－Lie algebras［J］.Acta Math Sinica：English Series，2007，23（5）：847－856.

Frattini subalgebras andc－supplemented subalgebras for Lie－like algebras1－st

WEN Qi－jun，XIAO Yu－shan
（School of Sciences，Changchun University，Changchun 130022，China）

In this present paper，initially Frattini subalgebras andc－supplemented subalgebras are developed for Lie－like algebras1－st，obtained some properties of the Frattini subalgebras andcsupplemented subalgebras and give their relationship.

Lie－like algebras1－st；Frattini subalgebrs；c－supplemented subalgebras

O 152.5

110·21

A

1000－1832（2011）04－0020－05

2010－06－30

国家自然科学基金资助项目（10701019）.

温启军（1973—），男，硕士，讲师，主要从事李代数研究；肖玉山（1964—），男，博士，教授，主要从事统计学研究.

陶 理）