线性双时滞广义系统时滞依赖H∞控制
杨 帆,周士玉,冯毅夫,张庆灵
(1.天津城市建设学院电子与信息工程系,天津 300384;2.天津城市建设学院土木工程系,天津 300384;3.吉林师范大学数学学院,吉林四平 136000;4.东北大学系统科学研究所,辽宁沈阳 110004)
线性双时滞广义系统时滞依赖H∞控制
杨 帆1,4,周士玉2,冯毅夫3,张庆灵4
(1.天津城市建设学院电子与信息工程系,天津 300384;2.天津城市建设学院土木工程系,天津 300384;3.吉林师范大学数学学院,吉林四平 136000;4.东北大学系统科学研究所,辽宁沈阳 110004)
研究了线性双时滞广义系统时滞依赖H∞控制器设计问题.利用线性矩阵不等式方法和Lyapunov-Krasovskii泛函相结合,给出了线性双时滞广义系统的一个有界实引理.在此基础上,给出了H∞控制器的设计方法和存在的充分条件.该控制器的设计使得在满足一定的条件下闭环系统是正则、稳定、无脉冲的,且从扰动到控制输出的传递函数的H∞范数不超过某个确定的上界.
时滞广义系统;时滞依赖;H∞控制;有界实引理;线性矩阵不等式
0 引言
时滞现象经常在控制系统的状态、控制输入或量测输出中遇到,引起系统不稳定及系统指标的衰竭.时滞广义系统具有广泛的应用背景,尤其时滞H∞控制已成为热点研究问题[1-5].时滞系统H∞控制涉及时滞独立和时滞依赖两种情况.时滞独立H∞控制条件一般较为保守,特别是当系统的时滞较小时;对于时滞依赖的H∞控制,为了降低系统对时滞依赖的保守性,有许多种方法.
E.Fridman利用广义模型变换和线性矩阵不等式方法,给出了时滞独立和时滞依赖H∞控制存在的充分条件,同时还研究了输出反馈H∞控制等问题[4].文献[6]利用积分不等式,构造了一个不仅与时滞状态有关,而且与时滞上界状态有关的Lyapunov-Krasovskii泛函,有效地降低了系统的保守性.文献[5]利用权矩阵的方法讨论了线性时滞广义系统的时滞相关H∞控制,文献[7]引入了一个新的Lyapunov-Krasovskii泛函,以严格矩阵不等式的形式设计了保守性较小的时滞依赖H∞控制器.
本文在文献[2-3,8-9]的启发下,通过构造一个新的Lyapunov-Krasovskii泛函,设计了一个具有更小保守性的H∞控制器.
1 系统描述
考虑如下线性时滞广义系统:
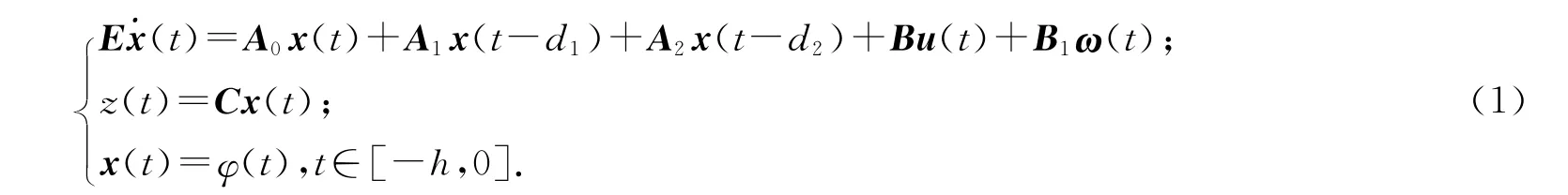
其中,x(t)∈Rn为系统的状态向量;u(t)∈Rl为系统控制输入向量,ω(t)∈Rq为系统扰动输入向量且ω(t)∈Lq2[0,∞);z(t)∈Rp为系统受控输出;φ(t)为系统的初始状态函数,A0,A1,A2,B,B1,C是已知适当维数常数实矩阵,矩阵E∈Rn×n且rank(E)=r≤n;未知时滞d j≥0但具有上界hj且0≤d j≤hj(j=1,2),

2 时滞依赖有界实

WT=ETP+SRT,R∈Rn×(n-r)为满足ETR=0的列满秩矩阵.则系统(1)是正则、无脉冲和稳定的,且对于非零扰动ω(t)∈Lq2[0,∞),系统(1)具有H∞性能指标γ.
证明定理的证明分两部分.首先证明系统是正则和无脉冲的.
由不等式(6),有



3 时滞依赖H∞控制
在定理1的基础上,讨论线性双时滞广义系统(1)的时滞依赖H∞控制问题.
定理2给定性能指标γ>0,时滞d1,d2∈[0,h],其中h是一个已知的正常数.给定矩阵G,如果存在正定对称矩阵P=PT>0,Q i=QTi>0,Z i=ZTi≥0(i=0,1,2,3)和矩阵S,F,T,使得如下的线性矩阵不等式(LMI)成立:

4 结论
本文研究了线性双时滞广义系统时滞依赖H∞控制器设计问题.对于两时滞系统,充分考虑了两个时滞的相互关系,构造了一个新的Lyapunov-Krasovskii泛函,并且没有进行系统模型变换,设计了一个具有较小保守性的H∞控制器,使得闭环系统是正则、稳定和无脉冲的且具有H∞范数界.
[1]LEE Y S,MOON Y S,KWON W H,et al.Delay-dependent robustH∞control for uncertain systems with a state-delay[J].Automatica,2004,40:65-72.
[2]王红,张友,王彩玲.一类中立时滞系统的带记忆输出反馈H∞控制[J].东北师大学报:自然科学版,2010,42(1):32-35.
[3]YANG FAN,ZHANG QINGLING.Delay-dependentH∞control for linear descriptor systems with delay in state[J].Journal of Control Theory and Applications,2005,1:76-84.
[4]FRIDMAN E,SHAKED U.H∞-control of linear state-delay descriptor systems:an LMI approach[J].Linear algebra and its applications,2002,(351/352):271-302.
[5]DU Z P,ZHANG Q L,LIU L L.Delay-dependent robust stabilization for uncertain singular systems with multiple input delays[J].ACTA Automatica Sinica,2009,35(2):162-167.
[6]PARK P G,KO J.Stability and robust stability for systems with a time-varying delay[J].Automatica,2007,43(8):1885-1858.
[7]WU Z G,ZHOU W N.Delay-dependent robustH∞control for uncertain singular time-delay systems[J].IET Control Theory and Applications,2007,1(5):1234-1341.
[8]张伟,时宝,盖明久.广义时滞系统的时滞相关型H∞控制[J].控制理论与应用,2009,26(12):1430-1434.
[9]何勇,吴敏.多时变时滞系统的鲁棒稳定及有界实引理的时滞相关条件[J].控制理论与应用,2004,21(5):735-741.
Delay-dependentH∞control for singular systems with two time-delays
YANG Fan1,4,ZHOU Shi-yu2,FENG Yi-fu3,ZHANG Qing-ling4
(1.Department of Electronic and Information and Engineering,Institute of Urban Construction,Tianjin 300384,China;2.Department of Civil Engineering,Institute of Urban Construction,Tianjin 300384,China;3.School of Science,Jilin Normal University,Siping 136000,China;4.Institute of Systems Science,Northeastern University,Shenyang 110004,China)
The problem of delay-dependentH∞control for singular systems with two state delays is concerned.In terms of linear matrix inequalities(LMIs)approach and Lyapunov-Krasovskii functional,it presents a delay-dependent bounded real lemma(BRL)to ensure the system to be regular,impulse free,and stable withH∞performance condition for two state delays.Based on this criterion,it obtains the sufficient conditions for the existence ofH∞state-feedback controller.
singular time-delay systems;delay-dependent;H∞control;bounded real lemma(BRL);linear matrix inequalities(LMIs)
TP 13
510·80
A
1000-1832(2011)03-0044-05
2010-04-22
国家自然科学基金资助项目(60574011).
杨帆(1966—),女,博士,教授,主要从事时滞广义系统鲁棒控制理论及应用研究.
陶 理)

