偏心轮腿六足机器人四足步态规划

万婷，王宇俊，李君科，何新强

(西南大学计算机与信息科学学院，重庆 400715)

偏心轮腿六足机器人四足步态规划

万婷，王宇俊，李君科，何新强

(西南大学计算机与信息科学学院，重庆 400715)

提出了一种适用于偏心轮腿六足机器人的直行四足步态规划.以一个运动周期为例，分析了偏心轮腿六足机器人直行过程中5个阶段的运动状态，以及每个运动状态中偏心轮腿步态的参数变化并用状态矩阵加以描述.将该步态用于所设计的偏心轮腿六足机器人，在驱动电机的控制下，能保证机器人的直行前进.

偏心轮腿六足机器人;步态规划;运动状态;状态矩阵;四足步态

0 引言

移动机器人是机器人的一个重要分支，它是一种集环境感知、行为控制与执行、动态决策与规划等多项功能于一体的高智能化机器系统.目前的移动机器人按移动方式可分为轮式移动机器人、履带式移动机器人、多足机器人.轮式机器人在道路平坦的环境中有着不可替代的主导地位，它具有高效、高速、承受能力强、易于控制等特性，而在沙地和泥泞不平整地面却有明显的不足.在这种环境下，履带式移动机器人能很好地适应沙地和泥泞地面，但是在类似山地和多障碍物的地面上时，履带式机器人也无能为力了.为了克服此类环境下的困难，人们又设计出了各种多足机器人.现在国内外具有代表性的多足机器人主要有:2005年研制的军用运输机器人“BigDog”，加拿大麦吉尔大学的MARTIN BUEHLER、美国密歇根大学的DANIEL KODIST CHEK和加州大学伯克利分校的FULL等人共同研制的Rhex，中科院沈阳自动化所开发的水下六足步行机，清华大学汪劲松等人研制的DTWN框架式双三足步行机器人、五足爬杆机器人，上海交通大学马培荪等人研制开发的JTUWM系列仿生哺乳动物机器人，哈尔滨工程大学研制开发的仿生机器人螃蟹，华中科技大学开发的“4+2”多足步行机器人等.不同的多足机器人的步态规划也有所不同，有效的步态规划能够保证机器人具有更强的地面适应性和稳定性，特别对于在不平整、无规则的地面行走的机器人尤为重要.本文以偏心轮腿六足机器人为例［1］，分析适用于该机器人的四足步态规划.

1 偏心轮腿六足机器人结构概述

偏心轮腿六足机器人采用对称性结构化设计，机身结构采用对称设计并呈扁平狭长体形.其内部封装了电池、电路等器件，行走机构分别为六个相同大小的偏心圆，均匀分布在机身的两侧，其中中间两个腿相对机身向外更突出，且每个行走机构由一个直流减速电机驱动，其结构如图1所示.考虑到偏心轮腿六足机器人用于不平整无规则地面，为保证其具有很好的越障能力及稳定性，采用了一种适用于该机器人的四足步态规划，使机器人在前进过程中始终保持腿在地面行走和腾空两种状态交替进行.

2 步态规划

2.1 步态的相关概念

为了研究多足机器人行走方式的需要，对动物的行走方式进行了大量的研究工作.通常人们把动物的行走方式叫作步态，而机器人科研人员把动物的步态借用到机器人领域，把机器人的步态定义为行走系统的迈步方式，即行走系统抬腿和放腿的顺序［2］.其中，美国非常有名的机器人学家MCGHEE在总结前人对动物步态研究的基础上，系统地给出了一系列描述和分析步态的严格的数学定义［3－5］.

步态相关概念和参数如下［6－7］:

(1)步态(gait)腿部摆动顺序及其时间相序等的步行模式;

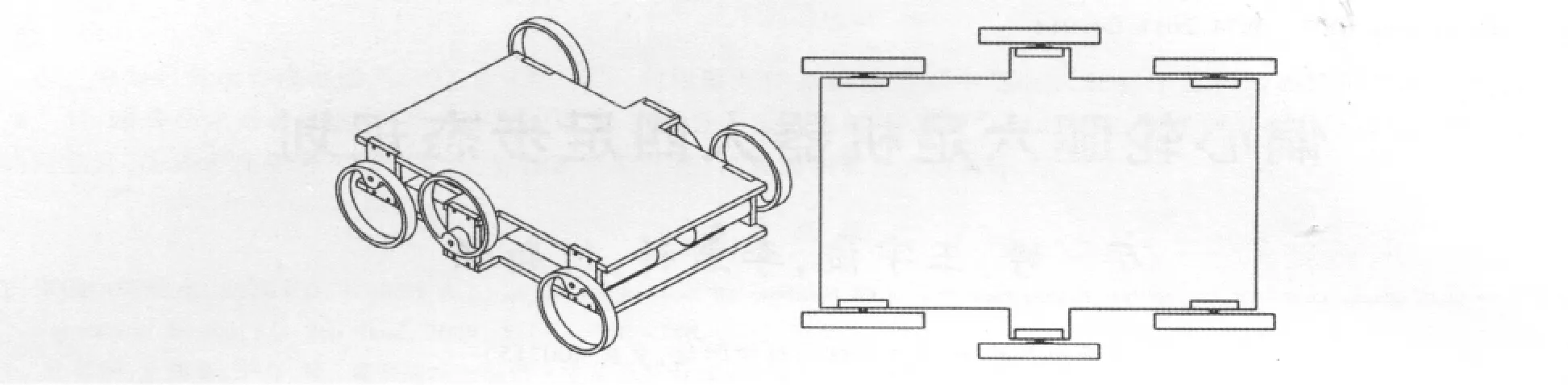
图1 偏心轮腿六足机器人结构Fig.1Structure of eccentric-type legged hexapod robot

(2)支撑相(support phase)腿部接触地面的状态，也称站立相;

(3)摆动相(swing phase)腿部抬离地面而处于空中的状态，也称摆动相;

(4)运动周期T(period of motion)周期步态中某一腿运动一个完整循环所需要的时间;

(5)有荷因数βi(load factor)腿i支撑在地面上的时间ti占整个运动周期T的比例，

(6)稳定系数δ(stability factor)描述步行进程中支撑足的平均个数，其中n为支撑足的个数，稳定系数等于n与有荷因数的乘积，即

2.2 典型的四足步态

六足昆虫在进行四足步态行走时，任一时刻保证有4条腿处于支撑相，而且是每一侧分别有两条腿处于支撑相，另外一条腿处于摆动相.假定六条腿中，左边三条腿按顺序分别为L1、L2、L3，右边三条腿按顺序分别为R1、R2、R3.典型四足步态的一个运动周期T分为三个阶段，每阶段所有腿的组合状态有所差异，分别是:当R1、R2、L1、L3处于支撑相时，R3、L2处于摆动相;当R1、R3、L2、L3处于支撑相时，R2、L1处于摆动相;当R2、R3、L1、L2处于支撑相时，R1、L3处于摆动相.如此交替实现六足昆虫的直行前进.考虑到一般情况下仿生六足昆虫机器人是从离散着地点、多自由度的腿的结构，采用典型的四足步态就能实现六足机器人的直行，但由于偏心轮腿六足机器人固有的行走机构，决定了典型的四足步态并不适合于该机器人.

2.3 偏心轮腿六足机器人四足步态规划

依据六足昆虫的行走特点，结合偏心轮腿六足机器人本身特有的行走机构，设计出本机器人的直行四足步态，该步态在一个运动周期T内分为初始状态、运行阶段1、调整阶段1、运行阶段2、调整阶段2.显然，机器人的直行包括前进和倒退两种情况，由于机器人采用对称设计和偏心圆腿的结构，所以对于机器人的前进和倒退而言，步态规划思想是一致的.因此，本文以前进状态为例，详细介绍偏心轮腿六足机器人的四足步态规划.

2.3.1 相关规定

为了描述方便，下面分别给出对偏心轮腿的旋转方向、临界点以及转速等相关约定.

(1)旋转方向假定机器人处于向前运动的状态时，从机器人右侧由外向里看，规定轮子顺时针旋转的方向为正方向，逆时针旋转的方向为负方向，如图2所示.

图2 偏心轮腿参数Fig.2Parameters of eccentric-type leg

(2)临界点临界点也就是偏心轮腿在支撑相状态和摆动相状态相互转换的一个过渡点.在机器人运动过程中，对每一个偏心轮腿而言，分别交替处于支撑相和摆动相，假定偏心轮腿处于正向方向旋转时，由摆动相状态过渡到支撑相状态时，偏心轮腿刚接触地面的点为P点，即正临界点;从支撑相状态过渡到摆动相状态时，偏心轮腿刚离开地面的点为Q点，即负临界点，PQ为偏心轮腿的着地范围.在引入临界点后，本文假定支撑相不包括P、Q两点，如图2所示.

(3)转速偏心轮腿以正方向旋转时，腿处于支撑相运动时的速度为w1，摆动相运动时的速度为w2，调整阶段时运行速度为w3.于是可构造偏心轮腿的状态矩阵Ni=［P，Q，S，M］T，i=1，2，3，4，5，6分别对应6条偏心轮腿的状态，左边三个腿编号为1、2、3，右边三个腿编号为4、5、6，P、Q、S分别指轮子处于正临界点、负临界点、支撑相.P、Q取值为1有效，S=1表示偏心轮腿处于支撑相，S=0表示偏心轮腿处于摆动相，M表示轮子旋转速度，取值为0、w1、w2或w3.

2.3.2 状态分析

下面针对偏心轮腿一个运动周期中的各个运动状态分别进行分析.

(1)初始状态2、3、4、5号腿处于正临界点，1、6号腿处于负临界点，速度为0.如图3中初始状态所示，此时状态矩阵

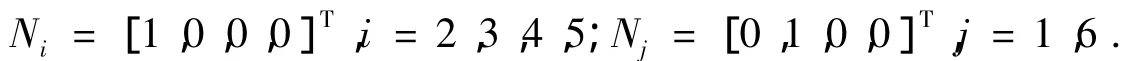
(2)运行阶段12、3、4、5号腿处于支撑相状态，并以速度w1正方向运动，同时1、6号腿处于摆动相状态，并以速度w2正方向运动，如图3中的运行阶段1所示，此时状态矩阵为

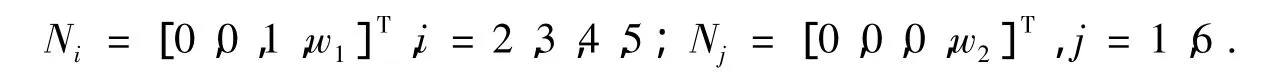
经过时间T后，2、3、4、5号腿处于负临界点Q，1、6号腿处于正临界点P.如图3中运行阶段1所示，此时状态矩阵

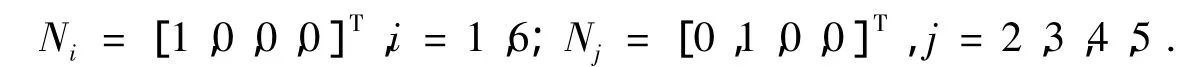
(3)调整阶段11、3、4、6号腿处于静止状态，2、5号腿从负临界点调整为正临界点，旋转方向为正方向，速度为w3，如图3中调整阶段1所示.此时状态矩阵为

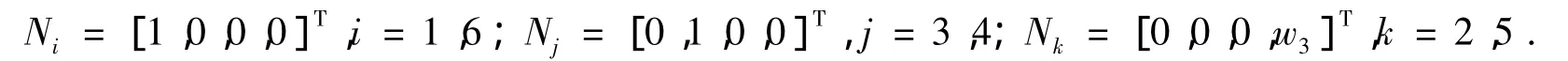
图3 运动周期T内偏心轮腿运动状态Fig.3Motion state of eccentric-type leg in period T

(4)运行阶段21、2、5、6号腿处于支撑相，并以速度w1正方向运动.同时3、4处于摆动相，以速度w2正方向运动，如图3中运行阶段2所示.此时状态矩阵为

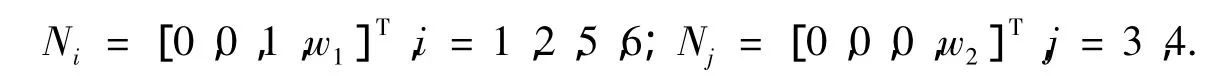
经过时间T后，1、2、5、6号腿处于负临界点，3、4号腿处于正临界点P.如图3中运行阶段2所示，此时状态矩阵为

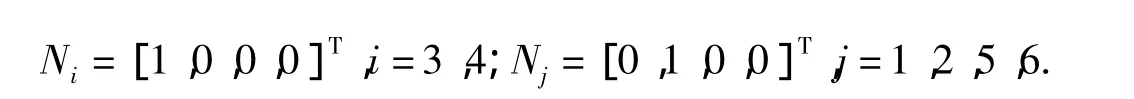
(5)调整阶段21、3、4、6号腿处于静止状态，2、5号腿从负临界点调整为正临界点，旋转方向为正，速度为w3.如图3中调整阶段2所示.此时状态矩阵为

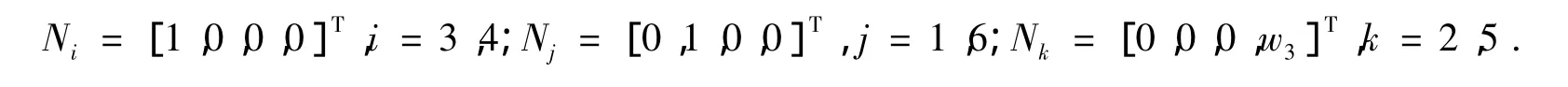
以上为周期T的运动状态描述，下一周期依次类推，不断重复阶段(1)～(5)，从而实现机器人直行前进的步态规划.

3 实验与分析

通过对四足步态稳定裕量的计算及其占地系数和稳定系数的分析可知，该步态用于偏心轮腿六足机器人上具有很好的稳定性，可以承受较大的载荷.在机器人的运行过程中，该步态确实能保证偏心轮腿六足机器人的直行前进.但四足步态也有不足之处，即速度相对较慢、效率不高.

4 结束语

本文所述偏心轮腿六足机器人步态规划，是在多足机器人设计思想的基础上，结合偏心轮腿提出的一种四足步态规划，通过对一个运动周期T中机器人的初始状态、运行阶段以及调整阶段的运动状态分析，可知该四足步态能很好地运用在偏心轮腿六足机器人上.然而，要保证机器人能高效稳定地在复杂多变的地形上前进，还需要进一步研究探讨.

［1］何新强，王宇俊，谭兴军.偏心轮腿六足机器人控制电路设计［J］.河南教育学院学报:自然科学版，2011，20(1):36－40.

［2］陈东辉，佟金，李重焕，等.人和动物的步态与步行机器人［J］.吉林大学学报:工学版，2003，33(4):121－125.

［3］MCGHEE R B.Some Finite State Aspects of Legged Locomotion［J］.Mathematics Bioscientes，1968(2):67－84.

［4］PREUMONT A，ALEXADRE P，GHUYS D.Gait analysis and implementation of a six leg walking machine［J］.Advanced Robotics，1991(2):941－945.

［5］LEE B H，LEE I K.The implementation of the gait and body structure for hexapod robot［C］//IEEE.Industrial Electronic.IEEE International Symposium on 2001，Washington D C:1959－1964.

［6］漆向军，陈霖，刘明丹.控制六足仿生机器人三角步态的研究［J］.计算机仿真，2007，24(4):158－160.

［7］冯巍，杨洋.慧鱼六足仿生机器人步态研究与实现［J］.机械设计与研究，2005(3):35－37.

Four-Footed Gait Planning of Eccentric-Type Legged Hexapod Robot

WAN Ting，WANG Yu-jun，LI Jun-ke，HE Xin-qiang

(College of Computer and Information Science，Southwest University，Chongqing400715，China)

A kind of robot four-footed gait planning is presented，which is suit for eccentric-type legged hexapod robot.Taking a movement cycle for example，analyzes on the five stages of eccentric-type legged hexapod robot in the process of motion，and uses state matrix to describe the change of parameters which is about the gait of eccentrictype leg in every movement state.Under the control of motor，the four-footed gait used in eccentric-type legged hexapod robot can ensure the robot go strait forward.

eccentric-type legged hexapod robot;gait planning;motion state;state matrix;four-footed gait

TP242.6

A

1007－0834(2011)04－0041－04

10.3969/j.issn.1007－0834.2011.04.014

2011－06－20

万婷(1988—)，女，湖北天门人，西南大学计算机与信息科学学院在读硕士研究生.