具偏差变元Rayleigh型p-Laplacian中立型微分方程周期解的存在性
邱本花,姚青华
(郑州科技学院基础部,河南郑州 450064)
具偏差变元Rayleigh型p-Laplacian中立型微分方程周期解的存在性
邱本花,姚青华
(郑州科技学院基础部,河南郑州 450064)
利用Mawhin连续定理和一些分析方法,证明了p-Laplacian中立型微分方程(φp(x(t)-cx(t-σ))')'=f(t,x'(t))+g(t,x(t-τ(t)))-e(t)周期解的存在性.
周期解;Rayleigh中立型微分方程;p-Laplacian算子;偏差变元
0 引言
在过去几年里,关于时滞微分方程周期解的存在性已经受到广泛的关注[1-6],如文献[3]研究了一个具有二阶时滞的微分方程

很少有文章讨论具偏差变元Rayleigh型的方程.文献[5]研究了下面的一个具有Rayleigh型的偏差变元方程

而且,通过利用Mawhin连续定理得到了方程(2)的周期解存在性的充分条件.
本文讨论了一个具有偏差变元Rayleigh型p-Laplacian中立型微分方程周期解的存在性.该方程为
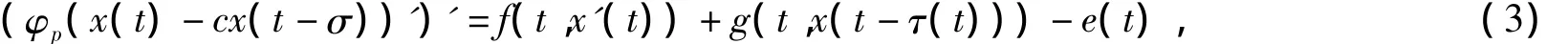

1 主要引理
首先定义以下几个概念.
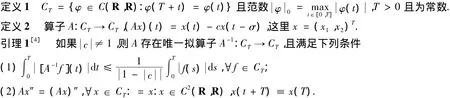
下面介绍本文的重要理论基础:重合度拓展定理.


2 主要结论





[1] CHEUNG W S,REN Jingli.On the existence of periodic solutions for p-Laplacian generalized Lienard equation[J].Nonlinear Anal TAM,2005,60(1):65-75.
[2] CHEUNG W S,REN Jingli.Periodic solutions for p-Laplacian differential equation with multiple deviating arguments[J].Nonlinear Anal TAM,2005,62(4):727-742.
[3] LU Shiping,GE Weigao.Periodic solutions for a kind of Lienard equation with a deviating argument[J].J Math Anal Appl,2004,289(1):231-243.
[4] LU Shiping,GE Weigao.Existence of periodic solutions for a kind of second-order neutral functional differential equation[J].Appl Math Comput,2004,157(2):433-448.
[5] DEL PINO M A,ELGUETA M,Manasevich R F.A homotopic deformation along p of a Leary-Schauder degree result and existence for')'+f(t,u)=0,u(0)=u(T)=0,p>1[J].J Differential Equations,1989,80(1):1-13.
[6] GAINES R E,MAWHIN J L.Coincidence Degree and Nonlinear Differential Equation[M].Berlin:Springer,1977.
Existence of Periodic Solution for Rayleigh Type p-Laplacian Neutral Function Differential Equation with Deviation Arguments
QIU Ben-hua,YAO Qing-hua
(Department of Basic Courses,Zhengzhou College of Science and Technology,Zhengzhou450064,China)
Using Mawhin's continuation theory and some analysis methods,the existence of periodic solutions of the p-Laplacian neutral function differential equation,(φp(x'(t)-c×(t-σ))')'=f(x'(t))+g(t,x(t-τ(t))) =e(t),is proved.
periodic solution;Rayleigh neutr function differential equation;p-Laplacian operator;deviating argument
O175.1
A
1007-0834(2011)04-0015-05
10.3969/j.issn.1007-0834.2011.04.006
2011-08-13
河南省基础与前沿技术研究计划资助项目(082300410070)
邱本花(1982—),女,河南信阳人,郑州科技学院基础部教师.

