三阶非齐次微分方程的研究

戴明清，冯 伟

(1.华北水利水电学院数学系，河南郑州 450011;2.河南教育学院数学系，河南郑州 450046)

三阶非齐次微分方程的研究

戴明清1，冯 伟2

(1.华北水利水电学院数学系，河南郑州 450011;2.河南教育学院数学系，河南郑州 450046)

通过构造K(t)，给出了一种三阶非齐次微分方程的解法.

特征方程;特解;常数变异法

对于形如x‴+a1x″+a2x'+a3x=f(t)的三阶常系数非齐次线性方程，其中ai(i=1，2，3)为常数，f(t)为闭区间[0，b]上的连续函数.由文献［1］可知，这种方程求解关键是找到一个特解，常用的方法是通过常数变易法求解.

设K(t)是相应的齐次方程x‴+a1x″+a2x'+a3x=0的一个解，且满足初值条件K(0)=0，K'(0)=0，K″(0)=1.由文献［2］可知，这样的解K(t)存在且唯一.

1 利用齐次方程特征根构造K(t)

定义满足代数方程λ3+a1λ2+a2λ+a3=0的根称为方程x‴+a1x″+a2x'+a3x=0的特征根.

证明 齐次方程x‴+a1x″+a2x'+a3x=0存在3个互不相同的实特征根λ1，λ2，λ3，则方程所有解可表示为x(t)=c1eλ1t+c2eλ2t+c3eλ3t.K(t)是方程的一个解，则一定存在常数c1，c2，c3，使得K(t)=++，并且满足初值条件K(0)=0，K'(0)=0，K″(0)=1，可得等式

其中A=(λ1－λ3)λ1λ3+(λ2－λ1)λ1λ2+(λ3－λ2)λ2λ3，则

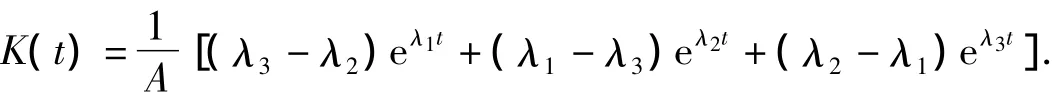
同理，容易得出以下3个引理.

引理2若齐次方程x‴+a1x″+a2x'+a3x=0存在3个实特征根λ1，λ2，λ3，且λ1=λ2≠λ3，则K(t)=

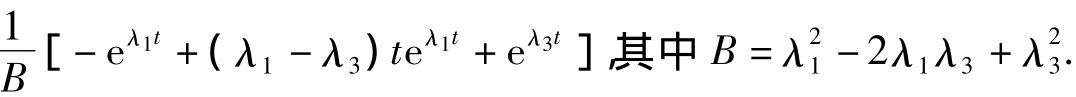
2 三阶常系数非齐次线性方程的常数变异公式

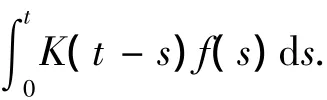
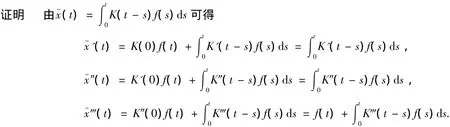
代入方程，则

3 三阶常系数非齐次线性方程的求解

由文献［3］，易得定理2.

定理2三阶常系数非齐次线性方程x‴+a1x″+a2x'+a3x=f(t)的通解为

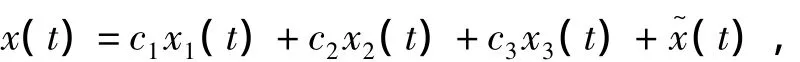
其中x1(t)，x2(t)，x3(t)为相应齐次方程的一组线性无关解组，x～(t)为非齐次方程的一个特解.

4 结论

常数变易法、待定系数法在很多时候不太实用，不是计算量太大就是对于f(t)的形式要求太苛刻.本文所给出的方法对于三阶非齐次微分方程实用性较强，只要根据其所对应的齐次方程的特征根的情况直接代入公式进行计算，对f(t)的要求大大降低.

［1］ 丁同仁，李承治.常微分方程教程［M］.北京:高等教育出版社，1994.

［2］ 王高雄，周之铭.常微分方程［M］.北京:高等教育出版社，2007.

［3］ 胡劲松，郑克龙.简化常数变易法求解二阶欧拉方程［J］.大学数学，2005，21(2):116－119.

Research on Non-Homegeneous Equations of Order Three

DAI Ming-qing1，FENG Wei2

(1.Department of Mathematics，North China University of Water Conservancy and Electric Power，Zhengzhou450011，China; 2.Department of Mathematics，Henan Institute of Education，Zhengzhou450046，China)

A solution is given for non-homegeneous equations of order three by generating K(t).

characteristic equation;special solution;constant-transform method

O175.1

A

1007－0834(2011)04－0013－02

10.3969/j.issn.1007－0834.2011.04.005

2011－09－05

河南省教育厅自然科学研究计划项目(2009A110004)

戴明清(1979—)，女，河南泌阳人，华北水利水电学院数学系讲师.