Boussinesq型方程初值问题局部解的存在性和整体解的不存在性

侯长顺，程 炜

(河南工业大学理学院，河南郑州 450052)

Boussinesq型方程初值问题局部解的存在性和整体解的不存在性

侯长顺，程 炜

(河南工业大学理学院，河南郑州 450052)

讨论了一类Boussinesq型方程ut+ux=σ(u)x+f(x，t)的Cauchy问题，利用Fourier变换和压缩映射原理证明了局部广义解和古典解的存在唯一性，并证明了整体广义解在半范数意义下的不存在性.

Boussinesq型方程;Cauchy问题;局部解;整体解

0 引言

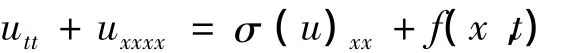
有多种方法得到了Boussinesq型方程utt+uxxxx=σ(u)xx的精确孤立子解，对于它们的初边值问题或初值问题，最近也有一些结果［1］.文献［1］重点研究了方程的初边值问题，在假设f∈H1(［0，T］;L2［0，1］)且f(0，t)=f(1，t)=0和σ∈R3，σ'(s)下有界，σ‴(s)满足局部Lipschitz条件且σ″(0)=0的情况下，证明了整体广义解u∈C(［0，+∞);H4［0，1］)∩C1(［0，+∞);H2［0，1］)∩C2(［0，+∞);L2［0，1］)的存在唯一性，并给出了解爆破的充分条件.该问题的物理意义详见文献［1］所引的文献.而对该方程的初值问题的研究尚未见到，本文在上述文献的基础上，研究(1)，(2)的初值问题:其中u(x，t)是未知函数，σ(s)是给定的非线性函数，f(x，t)为给定的函数，φ(x)，ψ(x)是已知的初始函数，下标x和t分别表示对x和t的导数.本文采用以下记号和概念，记Lp为通常的R上所有p次可积函数组成的空间，并赋予范数‖f‖p=‖f‖Lp(1≤p≤∞)，特别地，‖f‖=‖f‖L2;记Hs是通常的R上的Sobolev空间，具有范数‖u‖Hs=‖(1+)‖，表示其相应的齐次空间，具有半范数=，其中s∈R，I是单位算子，u^(ξ，t)是u(x，t)关于x的Fourier变换.

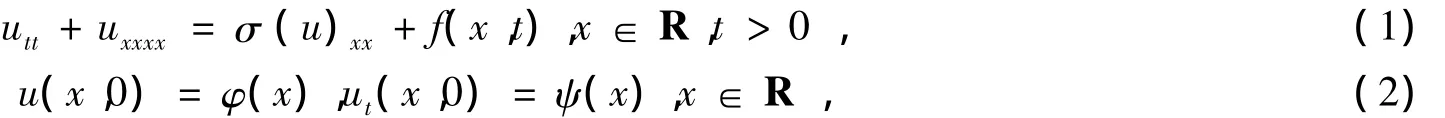
1 预备知识

引理1设f∈C［s］+1(R)，f(0)=0，s≥1，则对于u∈Hs，有‖f(u)‖Hs≤C1(‖u‖∞)，其中C1(‖u‖∞)是与‖u‖∞有关的常数.

引理2［2］设f∈C［s］+1(R)，s≥1.若u，v∈Hs，则‖f(u)－f(v)‖Hs≤C2(‖u‖∞)‖u－v‖Hs，其中C2(‖u‖∞)为依赖于‖u‖∞的常数.

2 问题(1)，(2)的局部解的存在唯一性

首先考虑线性问题

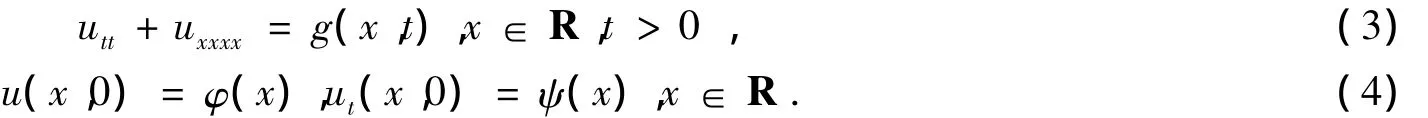
由(6)、(9)可知(5)式成立，引理得证.

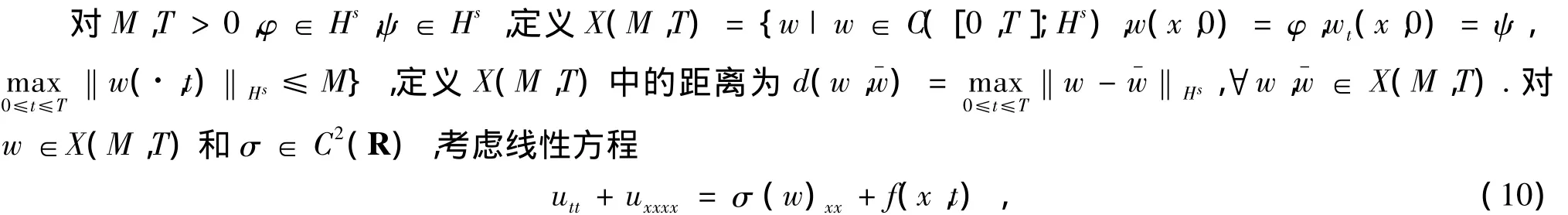
假定σ(0)=0，若不然，用σ(u)－σ(0)代替σ(u).定义S是把w映到方程(10)的唯一解的映射.下面证明对适当选择的M和T，映射S在X(M，T)中有唯一的不动点.

引理4设s≥1，φ∈Hs，ψ∈Hs和σ∈C［s］+2(R)，σ(0)=0，f∈L∞(0，T;Hs－2)，则对充分大的M和充分小的T，S映射X(M，T)到X(M，T).

证明对M，T＞0和w∈X(M，T)，由引理3得

引理5假设引理4的条件成立，则当M充分大和T相对于M充分小时，S映X(M，T)到X(M，T)是严格压缩的.

证明对M，T＞0和w1，w2∈X(M，T)，记u1=Sw1，u2=Sw2，w=w1－w2，U=u1－u2，显然U满足如下的初值问题t

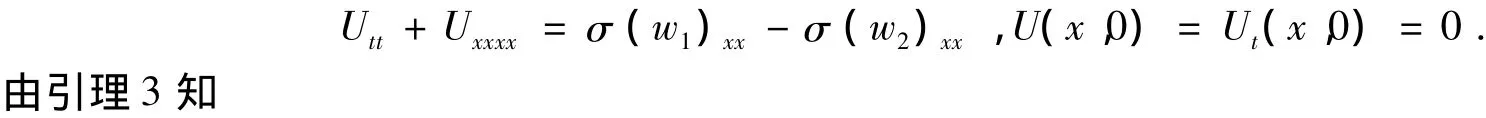
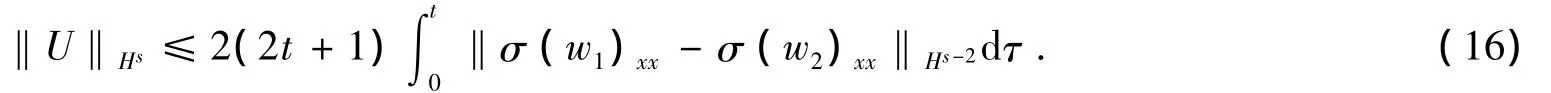
由Sobolev嵌入定理和引理2，得

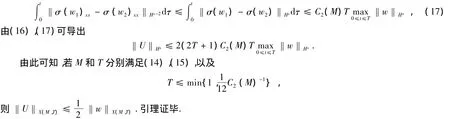
由压缩映射原理及解的延拓性定理，易得下面定理成立.

定理1设s≥1，φ∈Hs，ψ∈Hs，σ∈C［s］+2(R)，σ(0)=0和f∈L∞(0，T;Hs－2)，则问题(1)，(2)有唯一的局部广义解u(x，t)∈C(［0，T0);Hs(R))，其中［0，T0)是最大时间区间.

注1设u(x，t)∈C(［0，T0);Hs(R))是初值问题(1)，(2)的局部广义解，若f∈C1(0，T;Hs－2)且s＞9/2，则u(x，t)∈C(［0，T0);C4(R))是问题(1)，(2)的局部古典解.

3 问题(1)，(2)整体解的不存在性

文献［3］、［4］证明了Boussinesq-type方程utt+uxxxx=σ(u)xx的局部解u(x，t)∈H1∩H·－1的存在性，下面利用凸性原理证明该方程整体解的不存在性.

定理2假定引理7的条件成立.如果对∀s∈R，sσ(s)≤(4+8λ)ρ(s)，λ＞0且λ是常数，则下列条件之一成立时，问题(1)，(2)的整体解u(x，t)不存在，

如果E(0)＞0，利用类似于文献［6］所采用的变换，可证明定理2的(3).

［1］ CHEN Guowang，YANG Zhijian.Existence and nonexistence of global solutions for a class of non-linear wave equation［J］.Mathematical Methods in Applied Sciences，2000，23(2):615－631.

［2］ WANG Shubin，CHEN Guowang.Cauchy problem of the generalized double dispersion equation［J］.Nonlinear Analysis TMA，2006，64(1):159－173.

［3］ GUO Boling，MIAO Changxing.On inhomogeneous GBBM equation［J］.J Partial Differential Equation，1995，8(3):193－204.

［4］ VARLAMOV V.Existence and uniqueness of a local solution to the Cauchy problem for the Boussinesq equation［J］.Mathematical Methods in Applied Science，1996，19(8):639－649.

［5］ LIU Yachen，XU Runzhang.Global Wk，p(k≥3，1＜p＜∞)solution of semilinear pseudoparablic equation［J］.Journal of Harbin Engineering Univeisity，2005，26(2):277－279.

［6］ 王艳萍，郭伯灵.一类广义Boussinesq型方程Cauchy问题［J］.数学年刊，2008，29A(2):185－194.

Existence of Local Solution and Nonexistence of Global Generalized Solution for Cauchy Problem of Boussinesq-Type Equations

HOU Chang-shun，CHENG Wei

(College of Science，Henan University of Technology，Zhengzhou450052，China)

Cauchy problem of a class of Boussinesq-type equationsutt+uxxxx=σ(u)xx+f(x，t)is discussed.The existence and uniqueness of local generalized solution and classical solution are proved by Fourier transform and the contraction mapping principle.The nonexistence of global solution is proved in the meaning of semi-norm.

Boussinesq-type equations;Cauchy problem;local solution;global solution

O175.2

A

1007－0834(2011)04－0006－04

10.3969/j.issn.1007－0834.2011.04.003

2011－09－02

河南省教育厅自然科学研究基金(2009B110007);河南工业大学校基金(10XPT002)

侯长顺(1980—)，男，河南平顶山人，河南工业大学理学院讲师.