博弈论在高校篮球教学中的实践研究

陈 钦，兰伟强

(福建农林大学体育部，福建福州 350002)

博弈论在高校篮球教学中的实践研究

陈 钦，兰伟强

(福建农林大学体育部，福建福州 350002)

针对高校球类教学缺少应用型人文教育的教学模式，提出把博弈学理论运用到高校篮球教学中，通过教学实践，构建相关博弈模型，分析当前影响学生学习积极性的深层次原因，在此基础上，对篮球教学进行博弈设计，在篮球教学中充分发挥博弈的作用，有效地提高学生学习兴趣及合作组织能力.

篮球;博弈论;模型;混合策略;战略;高校

1 博弈论概述

“博弈论”译自英文Game Theory，是以抽象数学模型描述和研究带有对抗性行为的竞争态势，并给竞争各方提供对策方法的应用数学方法［1］.如同经济活动中的经营决策、市场竞争一样，将博弈论运用到篮球教学中，研究学生的合作意识、参与竞争意识、获取学习积极性的策略与方法.为了研究的方便，我们将篮球教学博弈系统的构成因素分为3部分，即硬件、软件和活件.硬件是指场地、设备、器材等投资方面，软件是指正常运转的规章、规则、体制等约束条件，活件则是指参与体育的各种人，如学生、教师等［2］.

2 博弈模型构建

2.1 学生上课的博弈模型

学生上篮球课是要付出一定成本的，如体力成本、对其他学科学习成绩的影响，以及由于上篮球课而失去的其他机会收益等，同样，通过篮球课的学习，学生也会获得一定的收益，如增强体质、提高组织协作能力，以及由此带来的连锁效益等.假定第i个学生的支付函数为Xi(其中i=1，2，…，n)，收益函数为Yi=(Si+Ci)(其中Si为增强体质，Ci为连锁效益等，i=1，2，…，n)，则学生的预期收益为(Yi－Xi).如何使函数(Yi－Xi)的值最大，就成了每个学生所关心的问题.为了研究方便，这里假定只有两个学生甲和乙，并设想由于“自然”的原因，在同等的环境条件下，甲有更大的收益机会，那么甲、乙两个学生上课的博弈模型如图1所示.

假如甲、乙二人都分别以1/2的概率选择积极上课，1/2的概率选择不积极上课.那么对甲学生来说，选择不积极带来的期望效用为:1/2×(S1+C1)+1/2×C1，选择积极所带来的期望效用为:1/2×(S1+C1－X1)+1/2×(S1+C1－X1).显然在完全信息下，只要选择不积极上课的期望效用大于或等于训练带来的期望效用，即X1≥S1/2时，作为一个理性的学生，就必然会选择不积极上课;而只有积极上课的期望效用大于不积极(X1＜S1/2)时，他才会选择积极上课，同样可以推出，乙学生也只有在X2＜S2/2时才会积极上课;而在X2≥S2/2时，他会想法偷懒以逃避缺乏效益的篮球课程［3］.

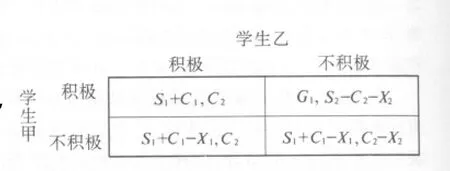
图1 两个学生上课的博弈模型Fig.1 Game model of two students in class

2.2 篮球教学过程中教师与学生的混合策略博弈

从整体教学效果角度来看，教师与学生之间也存在纳什均衡，即如果参与者中间的每一方都选定了自己的策略，同时如果对方保持自己的策略不变，而另一方任意修正自己的策略也不会得到任何好处的话，那么这样一系列的策略和随之而得到的结果就形成了纳什均衡.举个例子说，教师从集体利益出发要求学生积极听课、积极参与锻炼、互相配合等，而学生却追求着自己的利益，独自行动，采取不端正态度，于是教师与学生就会不断地陷入一系列的互相制约的困境中.而使用简洁的图表表述这些选择和结果，能使现实中教师与学生选择策略的各种可能性都在一个矩阵中充分展现出来.

假设教师对学生的规范达到了预期的目的，就假定教师得益为0(表示教师对学生的规范行为是分内的职责，规范好了不奖不罚，即得益为0);但是由于教师规范须投入成本，且规范不一定收到积极效果，因此，教师存在疏于规范的可能，如果教师疏于规范，学生仍能较好积极配合，就假设教师得益为A;如果在教师疏于规范情况下学生学习不利，就假设得益为－B，B的单位与A相同［4］.

对学生而言，按教师规范进行学习是其分内之事，故假设此时得益为0;但学生有直接参与篮球课的必要性与可能性，就存在不遵守教师规范的可能，如果此时没有受到教师的惩处，假设学生得益为C;若学生的违规行为受到教师惩处，假设学生的得益为－D，D的单位与C相同.根据以上假设，教师与学生在篮球教学过程中，因为各自的不同抉择而面临的不同困境，如图2所示.

图2 教师与学生的混合策略博弈模型Fig.2 Mixed strategy model of teacher and student

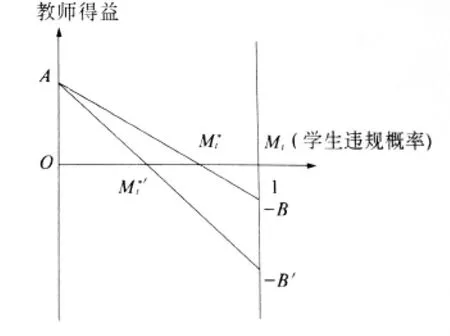
图3 学生的混合型策略Fig.3 Mixed strategy of student

分析图2中博弈矩阵，发现在篮球教学实践中没有双方都能接受的纳什均衡的策略组合.例如，教师与学生合作的选择方案就是表中的(0，0)选项，但是一旦其中一方试图为了让自己更好过一些而蠢蠢欲动，那么随之而产生的一系列的连锁反应，就不可避免地引入(C，－B).而(C，－B)这个格子所代表的恰恰就是一个纳什平衡.上述博弈中，解决窘境的方法就是让所有的参与方都能够同意协调各自的行动，而且各方面都能严格遵循所达成的协议.教师与学生都以一定的概率随机选择策略，双方都无法根据对方的选择方式，调整自己的策略获得利益，从而使得自己可能的最大化的损失最小化，即在概率分布的意义上达到一种稳定，或者说纳什均衡.这就构成了教师与学生之间的混合型策略博弈.

图3中横轴表示学生选择“违规”策略的概率Mt，它分布在0到1之间，学生选择“不违规”的概率等于1－Mt.纵轴则反映对应于学生“违规”的不同概率，教师选择“疏于规范”策略的期望得益.图3中从A到－B连线的纵坐标就是横坐标对应的学生“违规”、教师选择“疏于规范”的期望得益.

容易说明该线与横轴的交点就是学生选择“违规”的最佳水平，选择“不违规”的最佳概率则为1－首先，A到－B连线上每一点的纵坐标，就是在学生选择该点横坐标表示的“违规”概率Mt时，教师选择“疏于规范”策略的期望得益A(1－Mt)(－B)Mt.假设学生的“违规”概率大于，此时教师“疏于规范”的期望得益小于0，因此他一定会选择“规范”，从而学生违规一次被教师发现一次，因此对学生来说大于的“违规”概率是不可取的.反过来，如果学生“违规”的概率小于，则教师“疏于规范”的期望得益大于0，因此教师不会严格要求学生，此时即使学生提高一些实践中“违规”的概率，只要不大于，教师都会选择“疏于规范”，因此学生不用害怕被发现“违规”，由于学生在保证不被发现的前提下，“违规”概率越大收获就越多，因此他会使“违规”的概率趋向于，均衡点是学生以概率和1－分别选择“违规”和“不违规”.此时教师“疏于规范”和“规范”的期望得益都等于0.

同理，教师采用“规范”与“疏于规范”混合型策略概率分布，也可以用同样的方法来确定.结论如图4中的和1－是教师的最佳概率选择.

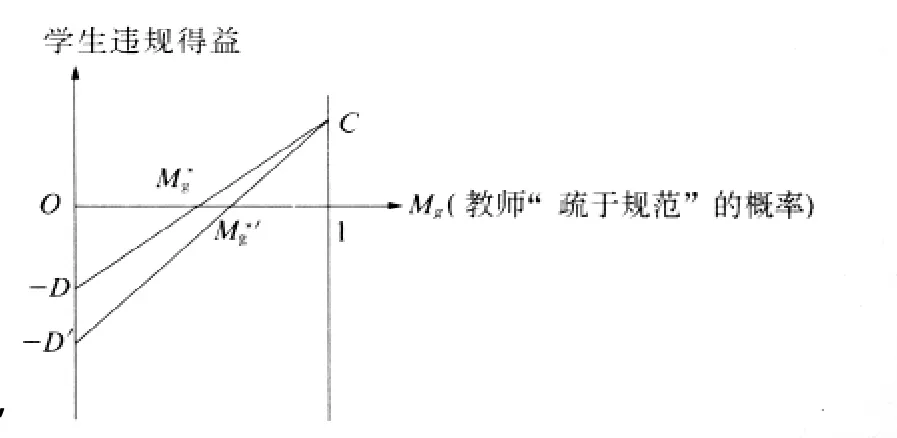
图4 教师的混合型策略Fig.4 Mixed strategy of teacher

在学生和教师的博弈中，学生分别以概率和1－随机选择“违规”与“不违规”，教师分别以概率和1－随机选择“疏于规范”与“规范”时，双方都不能通过改变策略或概率改善自己的期望得益，因此构成混合型策略纳什均衡，这也是该博弈唯一的纳什均衡.

2.3 篮球教学过程中教师与学生的混合策略博弈中“激励悖论”

如果在学生与教师的博弈之间加入惩罚或利益激励等，则博弈结果会有所不同.具体来说，为了限制学生课堂中的违规行为，教师可以加大对学生违规行为的惩罚力度，这样，对学生的惩罚会使得D增大，在图4中，这相当于－D向下移动到－D'.如果教师混合策略中的概率分别不变，此时学生“违规”的期望得益变为负值，因此学生会选择“不违规”.但是在教学过程中，学生减少“违规”现象，则会使教师更多选择“疏于规范”，最终教师的概率提高到，达到新的均衡，而此时学生“不违规”的期望得益又恢复到0，他会重新选择混合型策略.由于学生的混合策略概率分布是由图1决定的，并不受D值的影响，因此教师对学生实施惩罚在长期中并不能抑制学生的“违规”，可以增加学生的得益或对学生给予奖励.但从博弈中可以看出，这也不是长久之计.

目前教学过程中，如果教师对学生实施严惩，意味着D增加D'.此时，如果学生“违规”的概率不变，那么教师“疏于规范”的期望得益变为负值，教师一定会选择“规范”，学生只能减少“违规”的概率，直到将下降到此时教师又会恢复混合型策略，达到新的混合策略均衡.这里奖励与惩罚是相对的，故不再多加叙述.

在博弈过程中，教师与学生双方的最佳选择都取决于对方的选择.而对学生进行一定的惩罚或激励是有必要的，同时也解决了由学生行为引起的课堂教学方案优化问题.

3 篮球教学模式的博弈论设计

通过上述博弈模型分析可知，如何充分调动学生的积极性和学习兴趣、树立学生的自信心、最大限度地调动学生的潜在能力、充分发挥他们的长处释放其活力是学习关键所在.而教师作为教学过程中的主导，应为学生提供喜欢和感兴趣的篮球教学博弈比赛方式，为学生“行为”制定合理的博弈规则，给学生参与博弈提供准确信息，才能逐渐提高学生的兴趣，从而提高课堂教学效果.为此，以某人数为21人的班级进行4对4半场篮球比赛教学为例，进行博弈论设计.

3.1 组队博弈原则

首先对学生篮球技能水平进行综合测试，按学生不同的技能水平情况分为运动比赛型、游戏型、组织型、理论裁判型等.根据学生参与篮球教学比赛的需要，教师运用蛇形排列方法组队，设计不同水平、不同位置、不同技术和教学内容的菜单，使学生认识自己在集体中所处的位置，并根据自身的情况选择在博弈过程中要使用的技能，比如前锋、后卫等.

3.2 最大最小化原则

通过分组，各组进行单循环比赛，时间为10 min，每个队的成绩作为学生体育课的考核成绩依据之一，使学生充分了解队友和对手，所有的参与者必须将各种策略尽量组合，在投篮时无论是左移还是右移，都能得到自己希望的结果.在比赛时，还需要根据具体的情况随时调整，而且要根据自己的优势选择合适的比例.

3.3 博弈战略选择

战略是博弈理论的核心问题，在复杂多变、激烈竞争的攻守对抗中，队员们要学会观察场上攻守变化情况，了解对手特点，处理好攻守关系，发挥潜在能力，采用最优化策略，力争控制比赛的主动权［5］.

3.3.1 零和博弈

零和是博弈论里的一个概念，即双方博弈时，一方得益必然意味着另一方吃亏，一方得益多少，另一方就吃亏多少.之所以称为零和，是因为将胜负双方的“得”与“失”相加，总数为零.因此在零和博弈中各博弈方决策时都以自己的最大利益为目标，对每个组别来说，战胜对方都是唯一的选择.

图5 没有竞赛存在的学生支付矩阵Fig.5 Payoff matrix of students without competition

图6 有竞赛存在的学生支付矩阵Fig.6 Payoff matrix of students with competition

3.3.2 合作博弈

卡曾巴赫说过:“工作群体的绩效主要依赖于成员的个人贡献，而团队的绩效则基于每个人的不同角色和能力大小而产生的乘数效应.”篮球的教学活动和比赛方式都与团队合作密切相关，篮球教学和比赛中的关键因素包括位置、分工、配合等，因此，在篮球教学中对学生进行合作博弈能力的培养，是切实可行的.但是没有比赛的篮球教学不能进行合作博弈论实践运用，没有比赛的存在，小组成员可以选择合作，也可以选择不合作，支付矩阵如图5所示.合作可以使双方体验到篮球运动的乐趣，但不合作，双方也没什么损失;所以，以小组队员团队比赛为主要形式的考核评价方法，有利于

培养学生积极参与竞争、自发合作的精神，此时的支付矩阵如图6所示.合作可以使双方具有共同的奋斗目标、高度的一致性和团队精神，在运动中保持最佳的心理状态和“人际关系”，最终通过合作而获得胜利.另外，考核评价是教学的关键环节，考核评价方法的正确与否关系到整个教学质量的好坏，考核评价的目的不完全是检查学生知识技能的掌握情况，而更应注重学生掌握知识技能的过程和方法.因此应该淡化考评的选拔、甄别功能，强化检验、反馈、必要的约束和激励的综合功能，这样才有利于教学质量的进一步提高［6］.

［1］ 武振盛，李旭，辛克江，等.篮球比赛中“连胜"现象的博弈分析［J］.体育科技文献通报，2007(3):65－67

［2］ 孟阳，巫寿生.博弈论在网球发球策略中的应用［J］.福建金融管理干部学院学报，2006(2):62－64.

［3］ 王汉新，周辉.高校运动队训练与管理的博弈分析［J］.河北师范大学学报:自然科学版，2000，9(3):407－409.

［4］ ROGER A M.博弈论战略分析入门［M］.北京:机械工业出版社，2008.

［5］ 罗智波，陈文胜.论博弈论在体育比赛中的运用［J］.湖北体育科技，2004，23(4):433－435.

［6］ 戴珂.博弈论在高校球类教学中的应用［J］.体育学刊，2009，16(6):82－84.

Practical Study on Teaching of College Basketball by Game Theory

CHEN Qin，LAN Wei-qiang

(Department of Sports，Fujian Farming and Forestry University，Fuzhou350002，China)

In order to reform current modes of teaching of college ball games which are lacking in specific application type humanistic education，propose to apply game theory to the teaching of basketball，and constructs the relevant game model to analyze the deep-rooted reasons of the current impact of active learning through the teaching practice，on this basis，redesigns teaching modes of basketball by game theory，which fully exert the functions of basketball game teaching with distinctive game characteristics，in order to improve student interest in learning and cooperative capacity.

basketball;game theory;model;hybrid strategy;strategy;college and university

G841

A

1007－0834(2011)04－0078－03

10.3969/j.issn.1007－0834.2011.04.025

2011－05－17

福建农林大学本科教学改革项目(01JG04129)

陈 钦(1979—)，女，福建莆田人，福建农林大学体育部讲师.