两个小题目的启示

景慧丽，杨宝珍，张 辉

(第二炮兵工程学院基础部，陕西西安 710025)

两个小题目的启示

景慧丽，杨宝珍，张 辉

(第二炮兵工程学院基础部，陕西西安 710025)

由两道小题目的求解提出二重积分的中值定理的合理应用.

二重积分;积分中值定理;二次积分;极限;计算

有关二重积分的计算是一个难点问题，本文就两个题目的不同解答，提出要准确理解并合理运用二重积分的中值定理来解题.

下面的两道题，因为使用了不同方法，出现了两个不同的结果.哪个对?哪个错?错在哪里?

定理(二重积分的中值定理)［1］设函数f(x，y)在闭区域D上连续，σ是D的面积，则在D上至少存在一点(ξ，η)使得

解法1由于函数f(x，y)在闭区域}上连续，所以由二重积分的中值定理可得，存在(ξ，η)∈D，使得

此时，本题就无法继续进行下去了.

显然，解法1是正确的，其求解过程比较严密，无理论及计算错误.那么，解法2为什么是错的呢?错在哪里了呢?问题出在试图把二重积分计算出来这一步.由于被积函数是抽象函数，而且化为二次积分之后，被积函数与变量ρ及θ都有关系，既无法计算其具体的值又无法用变上限积分求导公式来解，因此该解法是错误的.

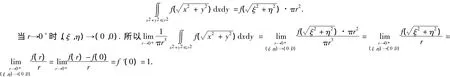
两种解法的结果截然不同.显然，解法1是正确的，其求解过程严密，无理论及计算错误.那么，解法2为什么是错的呢?错在哪里了呢?问题出在了

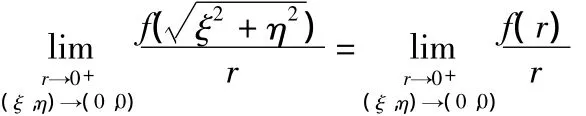
这一步.我们可以从两个方面来理解.

(1)由于当r→0+时，尽管点(ξ，η)→(0，0)，但是点(ξ，η)是以任意路径和任意方式趋于(0，0)的，而r是以直线的方式趋于0+的，所以点(ξ，η)及变量r不能用同一个变量来表示.

(2)由于ξ2+η2≤r2，如果把换成r，就意味着点(ξ，η)是在区域D的边界即ξ2+η2=r2上取得，显然和二重积分的积分中值定理不太一致，因为积分中值定理只说明点(ξ，η)的存在性，并没有说明点(ξ，η)在什么地方取得，更没说明一定在区域的边界上取得.因此解法2是错误的.

像这类把二重积分和求极限结合起来的题目，通常是以下述形式给出的，

其中m，n是大于零的整数.其解法可以总结如下:

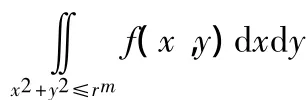
(2)如果m≥n，通常两种方法都可以用，但用二重积分的中值定理会更简单些.

不难验证，如果应用二重积分的中值定理会出现例2的情况，要么无法继续计算，要么计算错误.

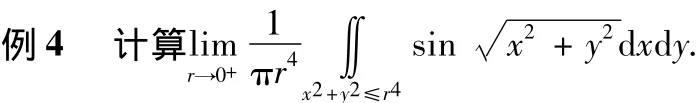
分析 由于m=n=4，显然m≥n，所以应先考虑应用二重积分的中值定理，因此

不难验证，如果先化简二重积分为二次积分然后再求极限结果也一样，但是过程略显繁琐.

［1］ 同济大学应用数学系.高等数学:下［M］.5版.北京:高等教育出版社，2002:78.

Inspiration from Two Small Exercises

JING Hui-li，YANG Bao-zhen，ZHANG Hui

(Department of Basic Courses，The Second Artillery Engineering College，Xi’an710025，China)

Proposed rational application of mean-value theorem of double integrals by solving two small exercises.

double integral;mean-value theorem of integrals;quadratic integral;limit;calculation

O172.2

A

1007－0834(2011)02－0015－02

10.3969/j.issn.1007－0834.2011.02.005

2011－03－14

景慧丽(1983—)，女，河南平顶山人，第二炮兵工程学院基础部教师.