杠杆式回转仪定量演示方法研究

林晓珑，张佳全，冯 毅

（吉林大学，吉林 长春 130022）

杠杆式回转仪定量演示方法研究

林晓珑，张佳全，冯 毅

（吉林大学，吉林 长春 130022）

在对杠杆式回转仪运动现象进行理论分析的基础上，通过测量出圆轮自转角速度，旋转轴进动角速度、进动角度的参数，定量研究了力矩与进动速度间关系、角速度与进动速度间关系、角动量定理的实验验证，最后将测量值与理论计算值进行了比较。将杠杆式回转仪运动状态的定量分析引入大学物理实验，培养了学生实际动手能力，加深了学生对角动量定理，力矩和角动量间关系的理解。

杠杆式回转仪；力矩；角动量；定量分析

绕旋转对称轴以很大的角速度转动的物体，如果没有外力矩的作用，由于惯性，物体转动轴的方向保持不变。迅速转动的陀螺受外力矩（如重力力矩）作用时，它并不是立即倾倒，而是转动轴绕着某固定轴缓缓转动。一个自转的物体受外力矩作用导致其自转轴绕竖直轴旋转，这种现象称为进动。

杠杆式回转仪是一种最常见的进动演示仪器，该仪器可以直观地演示出刚体的进动和陀螺的定轴性这一物理现象，几乎所有学校用它来演示进动，以加深学生对刚体角动量与力矩的关系的理解。也有人提出了一些改进的回转仪来更清楚的演示这一现象［1－2］，但是这些基本上都停留在定性的演示。如果能够对这一现象进行定量分析，学生通过测量各运动状态量，并经过自己动手计算各运动量之间的关系，将会对这一现象有更加深刻的认识，也培养了他们的动手能力与科学计算的素养。

1 杠杆式回转仪运动现象分析

1.1 杠杆式回转仪的结构与运动情况

杠杆式回转仪的结构见图1，装有圆轮的铁杆既能够绕着水平轴转动，又能和水平轴绕竖直轴旋转。配重块能沿着铁杆移动。如果对杠杆式回转仪进行仔细观察，会发现有如下主要现象：

图1 杠杆式回转仪结构图

（1）调节配重块的位置，使系统的重心通过支点，圆轮的自转轴处于水平方位，整个系统处于平衡状态。使圆轮快速转动，可以看到无论怎样旋转铁杆，圆轮的转轴方位始终保持不变，即角动量不变。

（2）调节配重物的位置，使系统的重心不过支点，即整个系统对支点轴受有重力矩作用。如果让圆轮绕铁杆旋转起来时，杠杆式回转仪就会产生进动现象。增大圆轮自转速度，进动速度将会减慢。改变圆轮的自转方向，铁杆的水平摆动角速度方向也随之改变。

（3）圆轮自转速度一定，如果移动配重块位置，进动速度也将发生变化。配重块越靠近旋转轴，进动速度也越大。

1.2 杠杆式回转仪运动的理论分析

下面对以上各现象进行理论解释，并推导出各运动量之间的计算关系。为了使得计算符号统一，这里我们规定，圆轮的自转速度为ω，φ为水平转动角度（即为进动角度），ωp为进动角速度，L为角动量，M为系统受到对支点O的外力距。

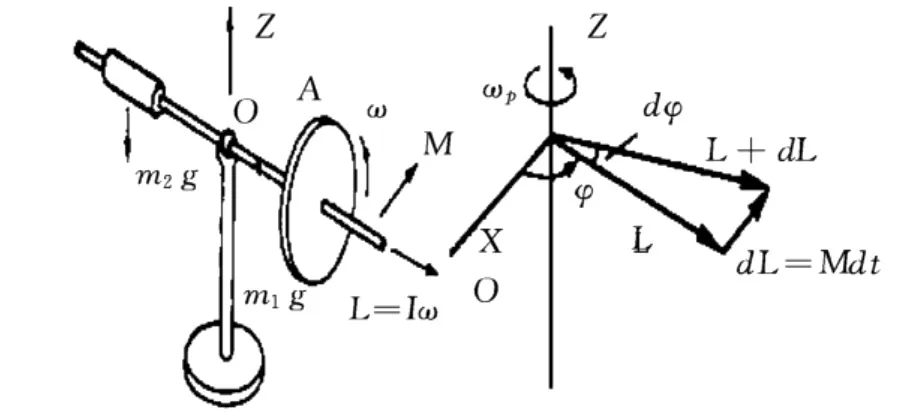
图2 杠杆式回转仪简化结构及符号规定

其中：M1，M2分别为圆轮和配重块重力所产生的力矩；m1，m2分别为圆轮和配重块质量；l1，l2分别为圆轮和配重块到支点O的距离。

对于圆轮的角动量增量可以表示为：

当系统不平衡时，整个系统受到对支点O的外力矩M的作用，则角动量不守恒。由角动量定律知，在时间内转轮对支点的自旋角动量L的增量为dL＝Mdt。在系统转轴水平情况下，转轮受到外力矩方向为水平向内，dt时间后，圆轮的角动量变成L＋dL＝L＋Mdt由于M，L和L＋dL的方向均在水平面内，所以自旋轴的方向不会向下倾斜，而仅是水平向内偏转。连续不断的偏转，就形成了进动。

对于杠杆式回转仪所受力矩可以视为配重块和圆轮重力产生力矩之和，表示为：

则进动角速度为

由角动量定理有

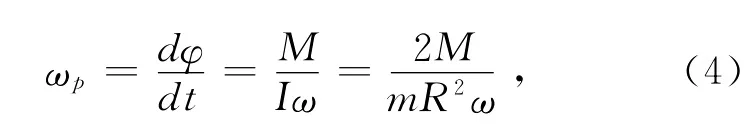
由上式可见，当力矩M一定时，圆轮自转速度越大，进动角速度越小；同时当圆轮自转速度一定，力矩M越大，进动角速度也将越大。

以上理论的推导是建立在角动量定理的基础之上，为了加深对角动量和力矩关系的理解，根据角动量定理，角动量的增量是力矩对时间的积累，则有：

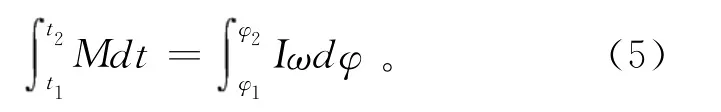
其中：φ2，φ1分别为t1和t2时刻铁杆旋转时所处角度。变换式（5），则有：

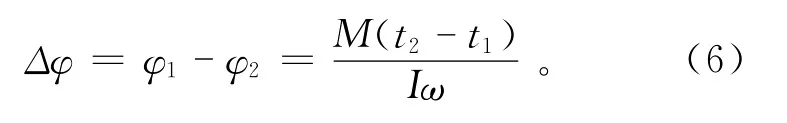
用式（4）、（6）就能够对回转仪各参数之间的关系以及角动量定理进行定量的讨论。

2 杠杆式回转仪各运动量的测量

杠杆式回转仪的运动量主要为圆轮的自转速度，圆轮绕竖直旋转轴Z转动的进动角速度和圆轮进动的角度，我们分别使用霍尔传感器、光电传感器和电位器型角度传感器来完成这些量的测定［3］。

2.1 自转角速度的测定

自转角速度的测定可以采用霍尔式传感器，测量方法如图3所示。在圆轮上按一定角度固定若干小磁铁，霍尔传感器固定在铁杆上，圆轮旋转时带动磁铁旋转。当磁铁经过霍尔传感器时，霍尔传感器产生电脉冲，通过记录各电脉冲之间的间隔时间可以间接测量出圆轮旋转角速度。即：其中：n1＝4为小磁铁的数量，小磁铁的数量不宜太多，太多会使传感器无法分辨，而导致检测失效。Δt1为检测到相邻电磁铁的时间间隔。

图3 定理测量的电路框图

2.2 进动角速度的测定

进动角速度的测量采用光电式传感器，在竖直轴轴套上固定一个光电传感器，在竖直旋转轴上固定挡片，挡片间隔为90°，竖直旋转轴转动时带动挡片旋转，其结构如图1所示。挡片依次通过光电传感器，光电传感器产生一个脉冲。通过计算相邻脉冲间隔时间就能准确的实现进动角速度的测量，即：

其中：n2＝4为均匀分布固定挡片数目，Δt2为相邻传感器挡光时间间隔，如果判断挡片挡光的顺序还能判断出进动的方向。

2.3 进动角度的测量

对于进动角度的测量可以选用电位器型角度传感器，传感器固定部分连接到竖直轴轴套上，滑动端接在竖直旋转轴上，如果在固定端两端加上固定电压U，则进动角度可以表示为：其中：U1为角度传感器输出电压，经放大、V/F变换后为数字量，由单片机计数。

3 定量实验结果分析

根据实验结果对理论分析进行验证。第一组依据式（6）来验证角动量定理，实验方法是：固定配重块，在不同自转角速度下，选取1s的时间验证进动角度的变化；在圆轮自转速度一定的条件下，移动配重块，验证1s时间进动角度的变化。第二组依据式（4）来验证力矩与进动速度之间的关系、自转速度和进动速度之间的关系，其中：车轮质量m1＝3.2kg，车轮半径R＝600mm，配重块质量为m2＝4kg，实验的结果见表1～表2。

表1 第一组验证角动量定理实验结果

表2 第二组验证各运动量关系实验结果

通过杠杆式回转仪的定量演示，使学生们对力矩和角动量等有了初步的认识，再通过计算各运动量的关系，对角动量定理，力矩与进动速度间关系、角速度与进动速度间的关系能有更进一步的理解。文中也对角速度和角度的测量方法进行了介绍，通过动手测量，计算激发学生探索理论联系实际的能力，拓展了知识面，对杠杆式回转仪运动状态的定量分析有着重要的意义。

［1］梁法库，路峻岭.力矩突变时角动量变化规律的实验演示与分析［J］.大学物理，2004，23（2）：42-43.

［2］梁法库，闫公敬.一种可自动改变力矩方向的课堂角动量定理演示实验［J］.大学物理，2005，24（12）：38-39.

［3］张佳全，冯毅.传感器测量转速物理演示装置的制作与研究［A］.2008年全国高等学校物理基础课程教育学术研讨会论文集［C］.2008.

Research of Lever Gyrostat Quantitative Demonstration

LIN Xiao-long，ZHANG Jia-quan，FENG Yi

（Jilin University，Jilin Changchun 130022）

This paper is based on the theoretical analysis of lever gyrostat movement，conducts a quantitative research on the relationship between the moment and procession speed，angular velocity speed and procession speed，and tests the angular momentum theorem through the measurement of the angular velocity speed of wheel rotation and revolving spindle procession，and the procession angle.It makes comparison between the measured value and theoretical calculation eventually.Applying the quantitative analysis of lever gyrostat movement tOthe university physics experiment，it improves students practical skills，and enhances their understanding of the angular momentum theorem，relationship between the moment and angular momentum.

lever gyrostat；moment；angular momentum；quantitative analysis

O313.3

A

1007-2934（2011）06-0046-03

2011-07-02