度量空间中六个映象的一个新的公共不动点定理
余 静,谷 峰
(杭州师范大学理学论,浙江杭州 310036)
度量空间中六个映象的一个新的公共不动点定理
余 静,谷 峰*
(杭州师范大学理学论,浙江杭州 310036)
在完备度量空间中,利用自映象对的相容和次相容性条件,讨论了一类φ-型压缩映象的公共不动点的存在性和唯一性问题,证明了一个新的公共不动点定理.文章结果改进和发展了Jungck,Diviccaro和Sessa,Kang,Cho和Jungck以及Ding的相关结果.
公共不动点;相容映象;次相容映象
0 引 言
在Jungck[1]中引入了相容映象的概念,它是可交换映象的推广.Park和Bae[2]扩展了具有相容性映象的一些公共不动点理论.Jungck[3]利用4个函数把Singh和Singh[4]的结果从交换映象拓广至相容映象.另一方面,Diviccaro和Sessa[5]利用Meade和Singh[6]中的压缩条件和Sessa[7]中的弱交换概念证明了四个映象的公共不动点定理.1990年,Kang,Cho和Jungck[8]利用映象的相容性证明了一个φ-型压缩型映象的公共不动点定理.同年,刘立山教授[9]引进了次相容映象对的概念,证明了几个公共不动点定理.
该文是上述工作的继续,利用自映象对的相容和次相容性条件,讨论了一类φ-型压缩型条件下六个映象的公共不动点问题,证明了一个新的公共不动点定理.该文的结果改进和发展了Jungck[3],Diviccaro和Sessa[5],Kang,Cho和Jungck[8]以及Ding[10]的相关结果.
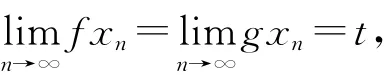
定义2[9]集合X上的自映象对(f,g)称为是次相容的,如果
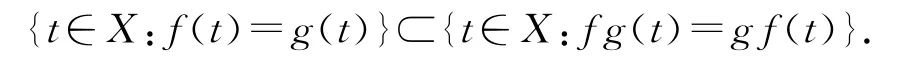
注1 由定义易知,可交换映象对必是相容映象对,而相容映象对也必是次相容映象对,但反之不真.反例可见[10].
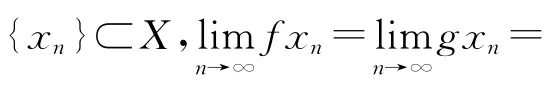
1 主要结果
1)φ是非减的且关于每个变元是上半连续的;
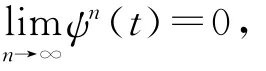
定理1 设(X,d)是完备度量空间,A,B,S,T,P和Q是X上的六个自映象,并有以下条件成立:
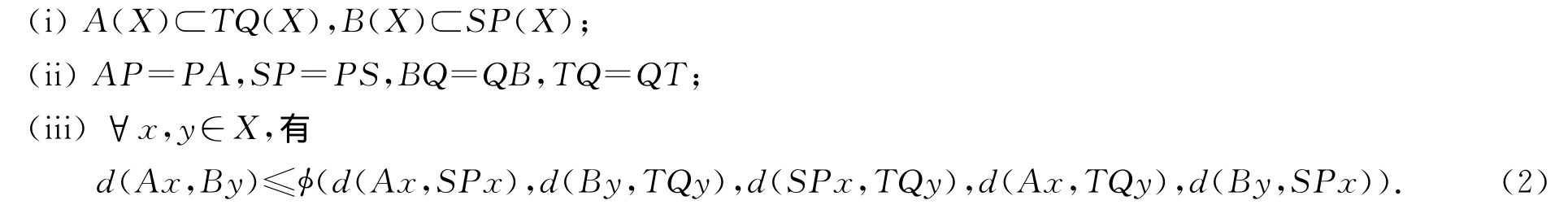
如果以下条件之一被满足,则A,B,S,T,P和Q有唯一公共不动点z.且z也分别是映象对(A,SP)和(B,TQ)的唯一公共不动点.
1)A,SP之一连续,且(A,SP)相容,(B,TQ)次相容;
2)B,TQ之一连续,且(B,TQ)相容,(A,SP)次相容;
3)S,T之一为满射,且(A,SP)和(B,TQ)都次相容.
证明 设x0∈X.因A(X)⊂TQ(X),B(X)⊂SP(X),∃x1∈X,使得y1=TQx1=Ax0;∃x2∈X,使得y2=SPx2=Bx1;…,归纳可得到X中的序列{xn}和{yn},满足

下证{yn}是X中的柯西列,为此只需证明{y2n}是X中的柯西列即可.事实上,假设{y2n}不是X中的柯西列,则必存在ε>0,使得对任意偶数2k,存在偶数2m(k)和2n(k),使得
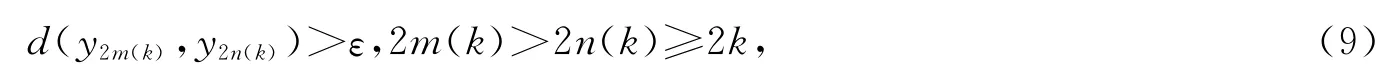
对任意偶数2k,设2m(k)是大于2n(k)且满足式(9)的最小偶数,即
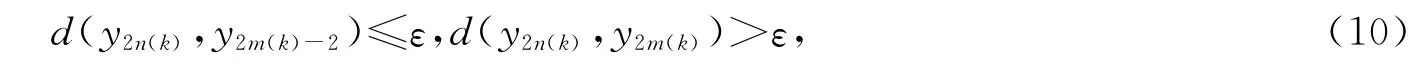
则对任意偶数2k,有ε<d(y2n(k),y2m(k))≤d(y2n(k),y2m(k)-2)+d2m(k)-2+d2m(k)-1,
由式(8)和(10),得

由三角不等式可得
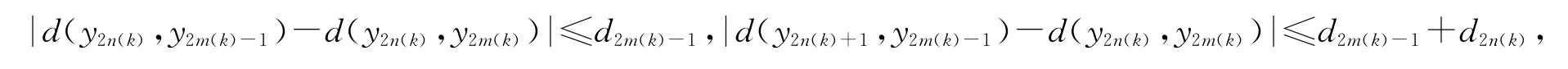
于是由式(8)和(11)可得
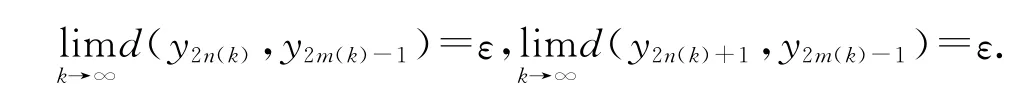
再由式(2)和(3)得
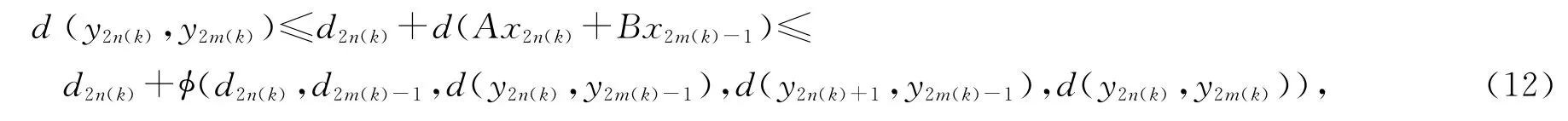
在式(12)中令k→∞,并注意到为φ的上半连续性得
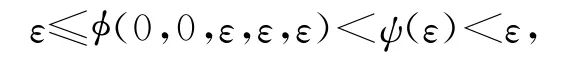
此为矛盾.因此{yn}是X中的柯西列.由X的完备性,不妨设yn→z∈X(n→∞),则子列{Ax2n},{SPx2n},{Bx2n-1}和{TQx2n-1}也都收敛到z.
1)设A,SP之一连续,且(A,SP)相容,(B,TQ)次相容.
先设SP是连续的.因为(A,SP)是相容的,从而由引理1有
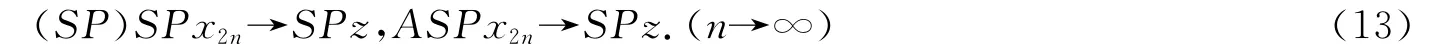
由式(2)得
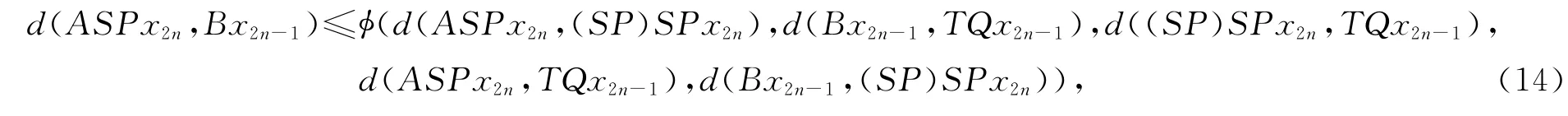
在式(14)中令n→∞,并注意到式(13),得
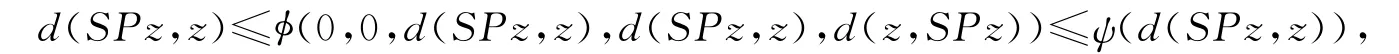
于是,由函数ψ的性质得d(SPz,z)=0,即z=SPz.再由式(2)得
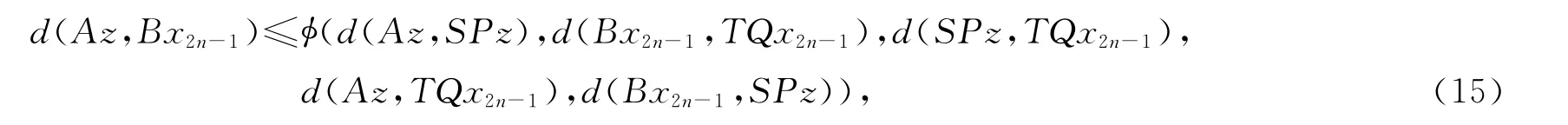
在式(15)中令n→∞得
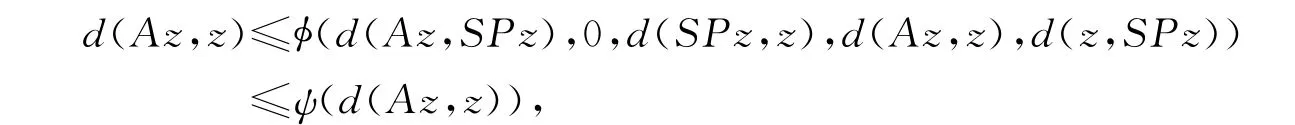
由函数ψ的性质得d(Az,z)=0,即使得Az=z.
因为A(X)⊂TQ(X),z∈TQ(X),因此存在u∈X,使得z=Az=TQu.于是由式(2)得
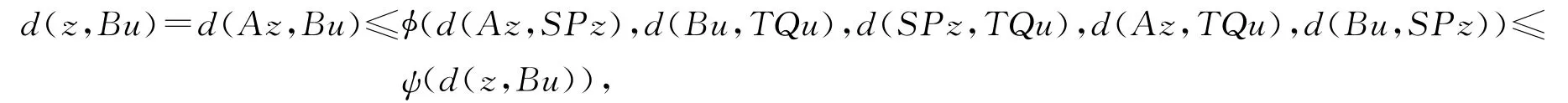
由函数ψ的性质,这意味着d(z,Bu)=0,即z=Bu,从而z=Bu=TQu.由(B,TQ)的次相容性得TQz=(TQ)Bu=B(TQ)u=Bz.
再由式(2)得
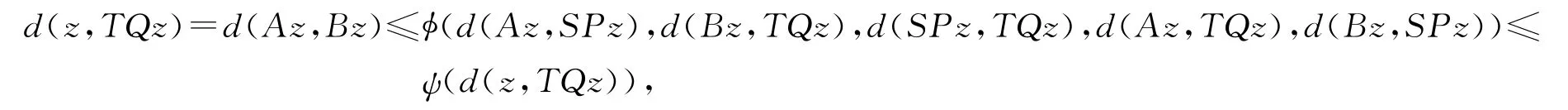
由函数ψ的性质可得d(z,TQz)=0,即z=TQz,进而有z=TQz=Bz.
综上可知,z=Az=Bz=SPz=TQz,即z是A,B,SP和TQ的公共不动点.
下面证明z=Sz=Pz=Tz=Qz.事实上,由AP=PA,SP=PS可得APz=PAz=Pz,(SP)Pz=P(SP)z=Pz.由式(2),并注意到z=TQz=Bz可得
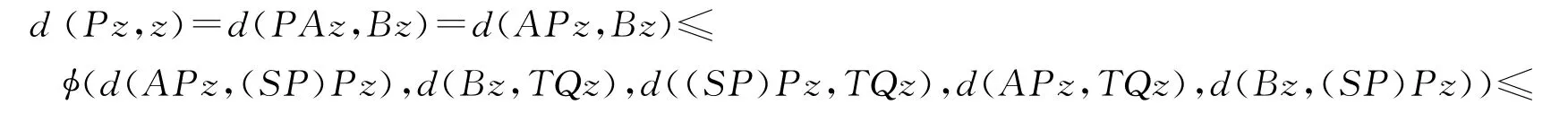
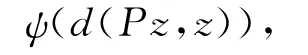
由函数ψ的性质可得d(Pz,z)=0,即Pz=z.又因为SPz=z,故得Sz=z.即z=Sz=Pz.
由BQ=QB,TQ=QT可得BQz=QBz=Qz,(TQ)Qz=Q(TQ)z=Qz.于是,由式(2)可得
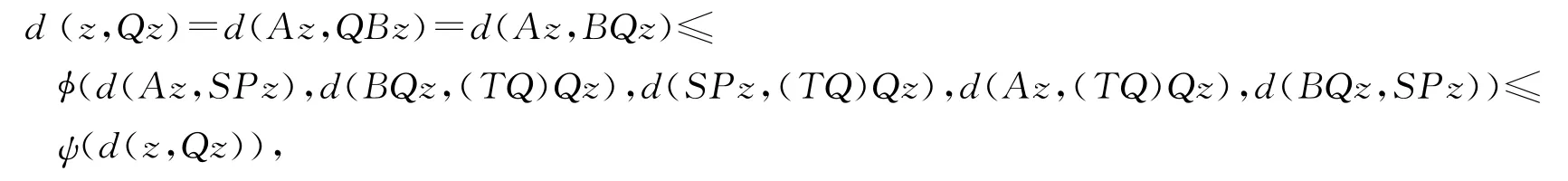
由函数ψ的性质可得d(z,Qz)=0,即z=Qz.又因为TQz=z,故得Tz=z.即z=Tz=Qz.
综上得到z=Az=Bz=Sz=Pz=Tz=Qz,即点z是A,B,S,T,P和Q在X上的公共不动点.
当A连续时,因为A和SP是相容的,引理1意味着{A2x2n}和{(SP)Ax2n}收敛到Az.由不等式(2)得
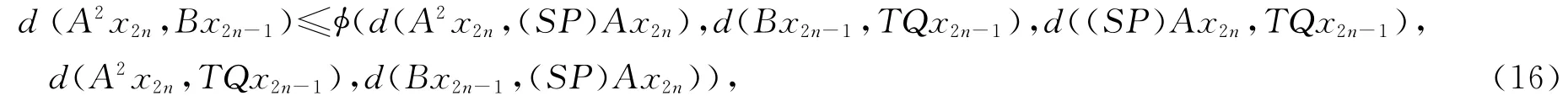
在式(16)中令n→∞得d(Az,z)≤φ(0,0,d(Az,z),d(Az,z),d(z,Az))≤ψ(d(Az,z)),
由函数ψ的性质可得d(Az,z)=0,即Az=z.
因为A(X)⊆TQ(X),故存在v∈X,使得TQv=Az=z.由不等式(2)得
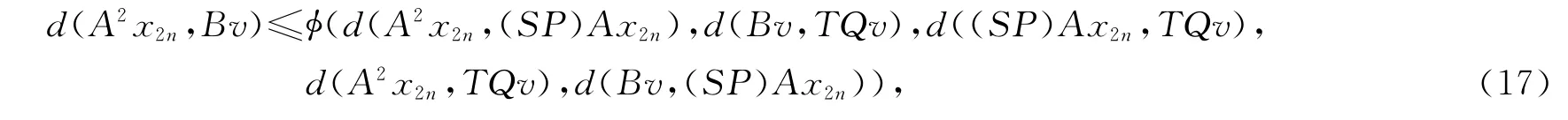
在式(17)中令n→∞得
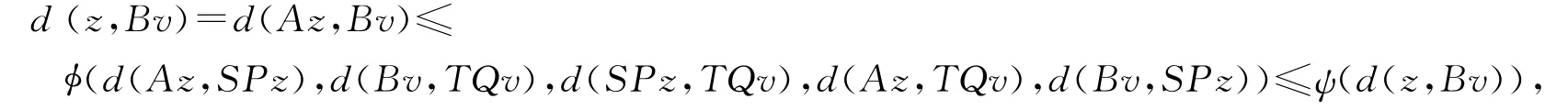
由函数ψ的性质可得d(z,Bv)=0,即Bv=z,进而TQv=Bv=z.因为B和TQ是次相容的,所以有(TQ)Bv=BTQv,这意味着TQz=Bz.再由不等式(2)得
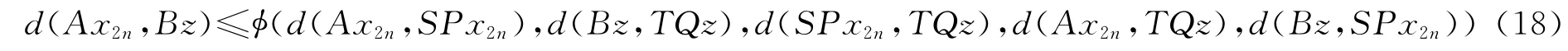
在式(18)中令n→∞,并注意到TQz=Bz得d(z,Bz)≤φ(0,0,d(z,Bz),d(z,Bz),d(Bz,z))≤ψ(d(z,Bz)),
由函数ψ的性质可得d(z,Bz)=0,所以z=Bz=TQz.
因为B(X)⊆SP(X),所以存在w∈X,使得SPw=Bz=z.由不等式(2)得
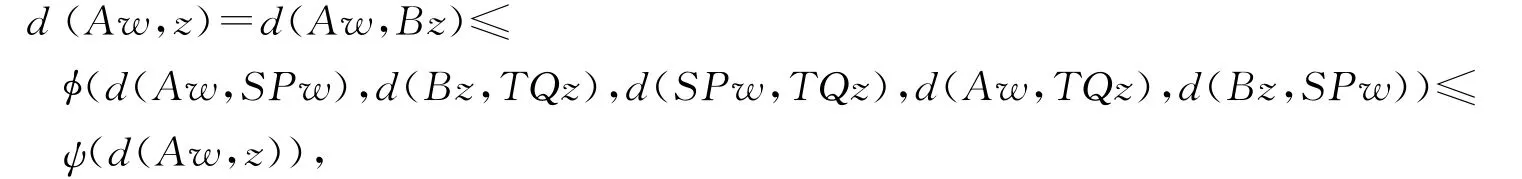
由函数ψ的性质可得d(Aw,z)=0,即Aw=z.进而SPw=Aw=z.因为A和SP是相容的,由引理1得(SP)Aw=ASPw,这意味着SPz=Az.
综上可知,z=Az=Bz=SPz=TQz,即z是A,B,SP和TQ的公共不动点.
同SP连续时相应部分的证明类似可证z=Sz=Pz=Tz=Qz,这样就证明了点z是A,B,S,T,P和Q在X上的公共不动点.
下证点z是A,B,S,T,P和Q在X上唯一的公共不动点,且z也分别是映象对(A,SP)和(B,TQ)的唯一公共不动点.
设z′≠z,z′∈X也是映象对(A,SP)在X中的一个公共不动点,由不等式(2)得
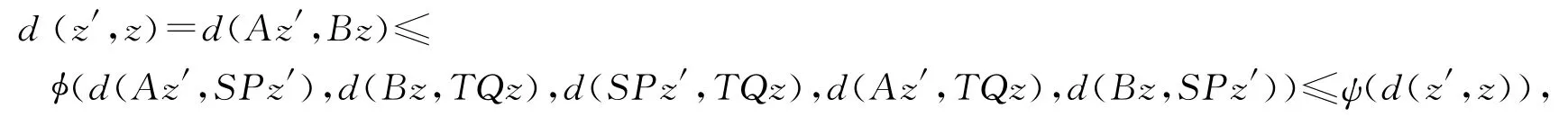
由函数ψ的性质可得d(z′,z)=0,即z′=z.因此z是映象对(A,SP)在X上唯一的公共不动点.同理可证z是映象对(B,TQ)在X上唯一的公共不动点.于是点z是A,B,S,T,P和Q在X上唯一的公共不动点.
2)当B,TQ之一连续,且(B,TQ)相容,(A,SP)次相容时,类似1)同理可证.
3)设SP,TQ之一为满射,且(A,SP)和(B,TQ)都次相容.
如果SP是满射,则对z∈X,∃μ∈X,使SPμ=z.由不等式(2)得
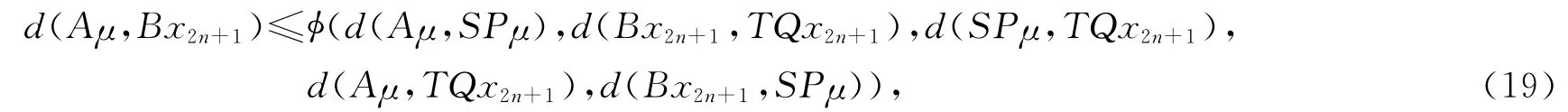
在式(19)中令n→∞得d(Aμ,z)≤φ(d(Aμ,z),0,0,d(Aμ,z),0)≤ψ(d(Aμ,z)),
由函数ψ的性质可得d(Aμ,z)=0,即Aμ=z.进而Aμ=SPμ=z.又(A,SP)次相容的,故有SPz=(SP)Aμ=A(SP)μ=Az.在式(19)中以z代替μ可得
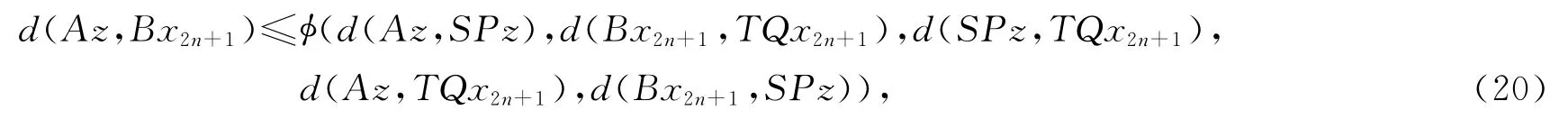
在式(20)中令n→∞得d(Az,z)≤φ(d(Az,z),0,0,d(Az,z),0)≤ψ(d(Az,z)),
由函数ψ的性质可得d(Az,z)=0,即得Az=z.进而Az=SPz=z.类似1)中相应部分的证明可证z是A,B,S,T,P和Q在X上唯一的公共不动点.且z也分别是映象对(A,SP)和(B,TQ)的唯一公共不动点.
当TQ是满射时同理可证z是A,B,S,T,P和Q在X上唯一的公共不动点.且z也分别是映象对(A,SP)和(B,TQ)的唯一公共不动点.
注2 定理1在以下三个方面改进和推广了Kang,Cho和Jungck[8]的相关结果:
1)把四个映象推广至六个映象;
2)把两对映象都相容减弱为一对相容另一对次相容;
3)定理1中的第3种情况并不要求任何一个映象连续.
推论1 设(X,d)是完备度量空间,A,B,S,T,P和Q是X上的六个自映象,并有以下条件成立:
(i)A(X)⊂TQ(X),B(X)⊂SP(X);
(ii)AP=PA,SP=PS,BQ=QB,TQ=QT;
(iii)∀x,y∈X,有
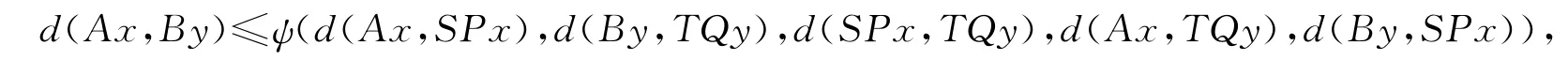
其中函数ψ满足以下条件:
(a)φ是非减的且关于每个变元是上半连续的;
(b)对任意t>0,ψ(t)=max{φ(t,t,t,t,t),φ(t,t,t,2t,0),φ(t,t,t,0,2t)}<t.
如果以下条件之一被满足,则A,B,S,T,P和Q有唯一公共不动点z.且z也分别是映象对(A,SP)和(B,TQ)的唯一公共不动点.
1)A,SP之一连续,且(A,SP)相容,(B,TQ)次相容;
2)B,TQ之一连续,且(B,TQ)相容,(A,SP)次相容;
3)S,T之一为满射,且(A,SP)和(B,TQ)都次相容.
定理2 设(X,d)是完备度量空间,A,B,S和T是X上的四个自映象,且有下面的条件成立:
(i)A(X)⊂T(X),B(X)⊂S(X);
(ii)∀x,y∈X,有
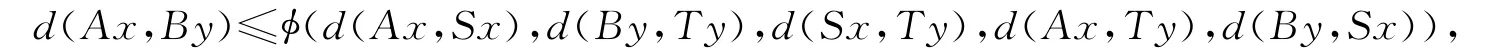
如果以下条件之一被满足,则A,B,S和T在X中有唯一的公共不动点z,且z也分别是映象对(A,S)和(B,T)的唯一公共不动点.
1)A,S之一连续,且(A,S)相容,(B,T)次相容;
2)B,T之一连续,且(B,T)相容,(A,S)次相容;
3)S,T之一为满射,且(A,S)和(B,T)都次相容.
证明 在定理1中取P=Q=I即得定理2.
注3 定理2在以下二个方面改进和推广了Kang,Cho和Jungck[4]的相关结果:
1)把两对映象都相容减弱为一对相容另一对次相容;
2)定理2中的第3种情况并不要求任何一个映象连续.
推论2 设(X,d)是完备度量空间,A,B,S和T是X上的四个自映象,且有下面的条件成立:
(i)A(X)⊂T(X),B(X)⊂S(X);
(ii)∀x,y∈X,有
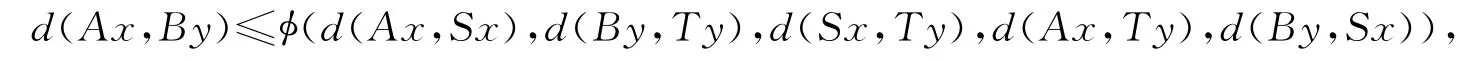
其中函数φ满足以下条件:
(a)φ是非减的且关于每个变元是上半连续的;
(b)对任意t>0,ψ(t)=max{φ(t,t,t,t,t),φ(t,t,t,2t,0),φ(t,t,t,0,2t)}<t.
如果以下条件之一被满足,则A,B,S和T在X中有唯一的公共不动点z,且z也分别是映象对(A,S)和(B,T)的唯一公共不动点.
1)A,S之一连续,且(A,S)相容,(B,T)次相容;
2)B,T之一连续,且(B,T)相容,(A,S)次相容;
3)S,T之一为满射,且(A,S)和(B,T)都次相容.
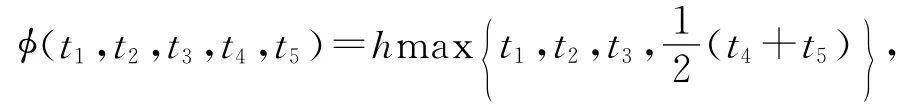
对任意的t1,t2,t3,t4,t5∈[0,∞)5和h∈[0,1),则相应结果是Jungck[3]中主要结果的改进和发展.
注5 定理1、2和推论1、2也改进和发展了Diviccaro和Sessa[5],Jungck[8]以及Ding[10]的相关结果,不仅用自映象对的相容和次相容性条件取代了可交换和弱交换条件,而且减弱了映象的连续性要求.
[1]Jungck G.Compatible mappings and common fixed points[J].Internat J Math &Math Sci,1986,9:771-779.
[2]Park S,Bae J S.Extensions of a common fixed point theorem of Mier and Keeler[J].Ark Math,1981,19:223-228.
[3]Jungck G.Compatible mappings and common fixed points(2)[J].Internat J Math &Math Sci,1988,11:285-288.
[4]Singh S L,Singh S P.A fixed point theorem[J].Indian J Pure Appll Math,1980,11(2):1584-1586.
[5]Diviccaro M L,Sessa S.Some remark on common fixed points of four mappings[J].Jnanabha,1985,15:139-149.
[6]Meade B A,Singh S P.On common fixed point theorems[J].Bull Austral Math Soc,1977,16:49-53.
[7]Sessa S.On a weak commutativity condition of mappings in fixed point considerations[J].Publ Inst Math,1982,32:149-153.
[8]Kang S M,Cho Y J,Jungck G.Common fixed points of compatible mapping[J].Internat J Math &Math Sci,1990,1:61-66.
[9]刘立山.(次)相容映象的公共不动点定理与广义Ishikawa迭代逼近定理[J].曲阜师范大学学报;自然科学版,1990,16(2):40-44.
[10]Ding Xieping.Some common fixed point theorems of commuting mappings II[J].Math Seminar Note,1983,11:301-305.
[11]Markowski J.Fixed point theorems for mappings with contractive iterate at a point[J].Proc Amer math Soc,1977,62:344-348.
A New Common Fixed Point Theorem for Six Mappings in Metric Space
YU Jing,GU Feng
(College of Scionce,Hangzhou Normal University,Hangzhou 310036,China)
In the complete metric space,by using the compatibility and weak compatibility condition of self-mapping pair,the paper discussed the existence and uniqueness of the common fixed point of a class ofφ-type contraction mapping and obtained a new common fixed point theorem.These results improve and develop the relevant results of Jungck,Diviccaro and Sessa,Kang,Cho and Jungck and Ding.
common fixed point;compatible maps;weakly compatible maps.
O177.91 MSC2010:47H06;47H10;47H17
A
1674-232X(2011)05-0393-06
10.3969/j.issn.1674-232X.2011.05.002
2011-01-11
国家自然科学基金项目(11071169);浙江省自然科学基金项目(Y6110287);杭州师范大学研究生教改项目;杭州师范大学研究生创新基金项目.
余 静(1986—),女,浙江慈溪人,应用数学专业硕士研究生,主要从事非线性泛函分析及其应用的研究.
*通信作者:谷 峰(1960—),男,辽宁沈阳人,教授,主要从事非线性泛函分析及其应用的研究.E-mail:gufeng99@sohu.com

