一类半正二阶三点边值问题正解的存在性
许也平
(杭州广播电视大学,浙江杭州 310012)
一类半正二阶三点边值问题正解的存在性
许也平
(杭州广播电视大学,浙江杭州 310012)
研究了一类半正二阶非线性常微分方程的三点边值问题正解的存在性,利用Krasnosel'skii锥拉伸锥压缩型不动点定理得到了正解存在的两个充分条件.
半正;三点边值问题;正解;存在性;不动点定理
1 引言及引理
非线性常微分方程边值问题是微分方程领域中的一个重要研究课题,在非线性扩散气体动力学、流体力学等学科中有重要应用.近年来,许多作者研究了非线性常微分方程三点边值问题正解的存在性[1-5].文献[1,4-5]中研究的都是非线性项非负的情形,该文讨论下列非线性二阶三点边值问题
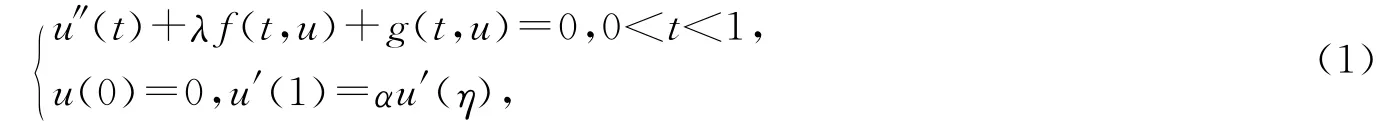
正解的存在性,其中λ>0,0<η<1,0<α<1.
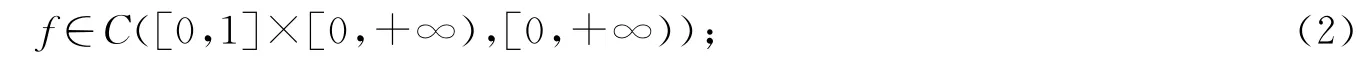
g∈C([0,1]×[0,∞),R),且存在M>0使
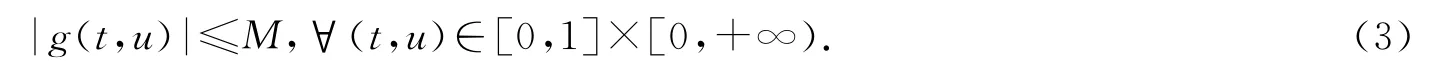
而由式(3)知问题是半正的,关于半正二阶三点边值正解存在性问题的研究较少.最近文献[6]研究了一类非线性二阶三点边值问题
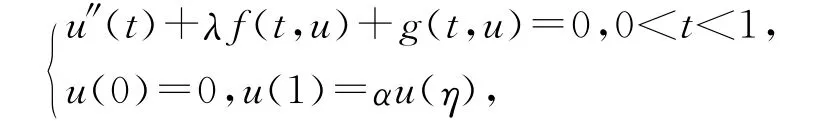
其中λ>0,α>0,0<η<1/α.文献[7]研究了一类非线性二阶三点边值问题
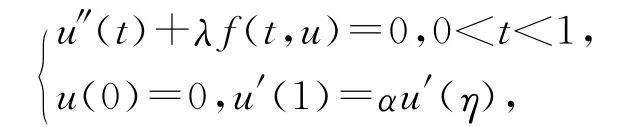
其中λ>0,0<η<1,0<α<1.受文献[6-7]的启发,在此研究半正问题(1)正解的存在性.注意到该文的方程与文[6]相同而边值条件与文[7]相同.该文的目的是证明,若f在无穷远处是超线性(或次线性)的,那么当λ充分小(或充分大)时边值问题式(1)至少有一正解.这里正解是指满足u(t)>0,∀t∈(0,1)的解.下面的Krasnosel’skii锥拉伸锥压缩型不动点定理在该文中起关键作用.其证明可参见文献[8].
定理1 设E是Banach空间,K⊂E是E中的锥.假设Ω1及Ω2是E的开子集,0∈Ω1且⊂Ω2.T:K∩\Ω1)→K是全连续算子.如果以下两条件之一成立:
(1)Tu≤u,∀u∈K∩∂Ω1;Tu≥u,∀u∈K∩∂Ω2.
(2)Tu≤u,∀u∈K∩∂Ω2;Tu≥u,∀u∈K∩∂Ω1.
那么T在K∩\Ω1)中至少有一个不动点.
先给出以下条件:
(H1)0<η<1,0<α<1;
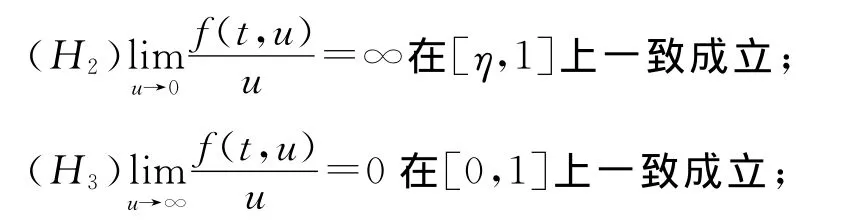

引理2[7]设(H1)成立,则对y∈C+[0,1]边值问题式(4)的唯一解u≥0;进一步,若存在t0∈(0,1)使y(t0)>0,则u(t)>0,0<t<1.
引理3 设(H1)成立,则对y∈C+[0,1],边值问题式(4)的唯一解u满足u(t)≥tu,0≤t≤1.
证明 设边值问题(4)相应的齐次方程的Green函数为G(t,s),则

引理5[6]设(H2)成立,定义F:[0,∞)→[0,∞)为


引理7[6]设式(2)(3)成立,那么由式(7)所定义的算子是全连续的且Tλ:K→K.
2 主要结果及证明
下面来叙述并证明该文的主要结果.
定理2 设式(2)(3)及(H1)成立,那么当λ充分小时,边值问题式(1)至少有一正解.
证明 令λ满足



[1]Khan A,Rafique M.Existence and multiplicity results for some three-point boundary value problems[J].Nonl Anal,2007,66(8):1686-1697.
[2]Liu Bingmei,Liu Lishan,Wu Yonghong.Positive solutions for singular second order three-point boundary value problems[J].Nonl A-nal,2007,66(12):2756-2766.
[3]Zhang Qiumei,Jiang Daqing.Multiple solutions to semipositone Dirichlet boundary value problems with singular dependent nonlinearities for second order three-point differential equations[J].Comput Math Appl,2010,59(8):2516-2527.
[4]Ma Ruyun.Positive solutions of a nonlinear three-point boundary value problems[J].Electron J Differential Equations,1999,1999(34):1-8.
[5]Liu Bing.Positive solutions of a nonlinear three-point boundary value problem[J].Appl Mathe Comput,2002,132(1):11-28.
[6]孙永平.一类半正二阶三点边值问题正解的存在性[J].浙江师范大学学报:自然科学版,2004,27(4):329-333.
[7]刘玉玲.一类半正二阶三点边值问题的正解存在性[J].纺织高校基础科学学报,2006,19(3):256-263.
[8]郭大钧.非线性泛函分析[M].济南:山东科学技术出版社,1985:310-311.
Existence of Positive Solution for A Semi-Positive Second-Order Three-Point Boundary Value Problem
XU Ye-ping
(Department of Fundamental Courses,Hangzhou Radio &TV University,Hangzhou 310012,China)
This paper investigated the existence of positive solutions for a semi-positone second-order three-point boundary value problem and obtained two sufficient conditions that guarantee the existence of the positive solutions by using Krasnosel’skii fixed point theorem.
semi-positone;three-point boundary value problem;positive solutions;existence;fixed point theorem
O175.8 MSC2010:34B10;34B15;34B18
A
1674-232X(2011)05-0411-05
10.3969/j.issn.1674-232X.2011.05.006
2011-03-11
浙江省教育厅科研基金项目(Y200804663).
许也平(1962—),男,浙江萧山人,副教授,主要从事微分方程及其应用研究.E-mail:xuyep@126.com

