速度与速率的定义在物理教学上所造成的迷思

邱韵如

(长庚大学通识教育中心物理科,台湾桃园)

速度与速率的定义在物理教学上所造成的迷思

邱韵如

(长庚大学通识教育中心物理科,台湾桃园)

速度 (velocity)和速率(speed)在物理教学中是非常重要且基本的概念.物理教科书对这二者的定义是不同的.前者和位移有关,是向量,有方向;后者和路径长有关,是纯量(即标量—编者注),没方向.为了让学生了解其差别,教科书及相关教材都举了很多的例题及考题来帮助学生学习.本文作者透过访谈,了解不同年龄层及知识背景的人,包括从小学生到成人,对速度和速率的概念及想法.探讨的问题包括:速度与速率的定义在教学上所造成的迷思、一般人对速度与速率的认知、英文里速度与速率的差别等等.

速度;速率;教材教法;迷思概念

1 前言

1.1 速度与速率有什么不同?

速度和速率有什么不同?对正在学习中学物理的学生来说,最直觉的回答是:一个有方向,一个没方向.再进一步思考,可能会说:一个和位移有关,一个和路径长有关.同样的问题,对初三以下的学生或已经忘了物理老师教过什么的人士来说,他们的答案通常是:速度大概是快慢的意思,而速率不是没听过,就是不知道什么意思.

1.2 速度和速率,哪一个比较常听到?

对绝大多数的人来说,“速度”比较口语化,所以一般在讲话或写文章时,用“速度”的机会比“速率”来得多.一项研究[1]指出,小学五年级以下的小朋友,大概知道“速度”是快慢的意思,但却几乎没听过“速率”这个名词.笔者访谈过不少非物理专业背景的成年人,他们也同样是常听到“速度”,而极少听过“速率”,他们认为速率是专业的学术词语或有特殊的定义,还有人认为速率的“率”是频率的意思.笔者访谈一位初一的学生,他马上背出速度就是距离除以时间,他说他的数学老师在上课时讲的都是速度,但课本却写速率,因此他认为速率和速度的意思是一样的.初三及高中的学生,大都知道速度与速率不同,他们不太记得定义,大都说“速度”是指快慢,而在课本之外,很少听到“速率”.

1.3 velocity和 speed,哪一个比较常见?

在物理课本上,速度是 velocity,速率是 speed.从字源来说,velocity是 15世纪左右从拉丁文来的,而 speed只是日常的口语.11世纪到 18世纪的学术著作,几乎都是以拉丁文撰写,这应该就是物理教科书中用 v来代表速度或速率的原因.物理老师通常会以为 velocity是很常见甚至是通俗的字,但笔者请教过一些英文老师、外国人及曾在国外教过物理的物理老师发现其实不然,他们都说速度就是speed,是日常生活常用的字,用来形容快慢,但是很少听到或甚至没见过 velocity这个字,他们认为velocity是很文言或专业的字.

2 速度与速率的定义在教学上所造成的迷思

2.1 平均速度的大小不等于平均速率?

物理课本里,平均速度定义是位移除以所需的时间,这样的定义和生活经验是不一致的.举例来说(图1),在台湾搭自强号火车从台北到花莲需要花 3小时,根据课本的定义,平均速度等于台北到花莲的位移 (117公里)除以 3小时,算出来的数值(39公里 /小时)(还要写出方向)有实质的意义吗?当然是要计算实际台北到花莲的路径长 (196公里)除以 3小时,算出来的数值 (65.33公里 /小时),也就是平均速率才有意义!在这个例题中,二者的大小并不相等,哪一个才可以真正代表火车的快慢?

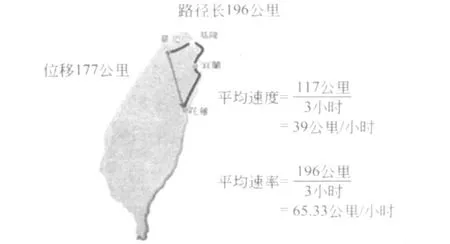
图1 台北到花莲的位移及路径长

2.2 平均速度的大小不能代表运动的快慢?

台北到花莲自强号的例题凸显了一个问题:平均速度的定义和生活经验相矛盾,它的大小不仅不等于平均速率,而且也不能代表火车运动的快慢,我们不禁要问,物理课本这样定义的目的何在?

再举个例子:某一时钟其秒针长为 10cm,秒针由 10走到 12期间,针尖之平均速度大小为多少 cm/s?这一题的答案要用秒针尖端点的位移(=10cm)除以时间 (10sec),所以答案是 1cm/s(别忘了还要标示方向).虽然这题的目的是让学生熟悉平均速度的定义,但是,如果把题目改成秒针从 9走到 12,或者从 6走到 12,算出来的平均速度的大小都会不同.我们当然不能解释成秒针在绕一圈的过程中,走得快慢会有所不同,但是,说平均速度的大小不能代表运动的快慢,似乎和课本的说法不太一致.那么,问题的症结是什么呢?

2.3 小学的速度和初高中的速度不一样?

再来看一个大家都很熟悉的例子.山路长 3公里,小明上山花了 2小时,下山花 1小时,请问小明的速度是多少?小学的自然课和数学课都是用“速度”来描述物体运动的快慢,并让学生学到速度和距离及时间的关系.小学教科书里的速度,其实就是中学物理课本里的“平均速率”.因此,以小学六年级的数学来算,来回山路的总长 (6公里)除以上下山总共花的时间 (3小时),因此答案是 2公里/小时.如果这一题出现在初三或高中的考卷里,学生就要回答,平均速度是零,平均速率是 2公里 /小时.同样的题目,有不同的解答,问题出在哪里?

速度的定义,小学和初中不一样,数学和物理也不同,这样显然是违背了九年一贯的精神.小学和初中的定义不一致的现象,让小学相关课程的教材编辑者及教师限于两难的境地,既不好太强调速度和速率的差别,又不敢大胆说速度和速率一样,以免和物理的定义相违背.

小学六年级的数学课教到“速度等于距离除以时间”的单元时,大都是用“速度”而较少用速率.高年级自然课本里讲到运动的快慢时,也都是用“速度”.小学的速度,其实就是中学物理课本里的“平均速率”.在初中及高中的物理课中,速度是向量,包括大小和方向,定义为位移除以时间,又说速度的大小就是速率.但是上述几个例子,根据定义所算出的平均速度和平均速率的大小并不相同,到底哪里出了问题?是物理上的定义有问题?还是教材教法上出了问题?

2.4 特别强调平均速度的定义

为了要说明平均速度和平均速率的不同,某高中物理课本特别举了这样的例题 (图2):某人沿着周长 400m的运动场,由 A点逆时钟跑了半圈到达正北方的 B点,共花了 40s,则此人跑步之平均速率是多少?平均速度是多少?根据定义,平均速率是 5m/s,平均速度是 2m/s(向北).教科书的作者在课文中以这个例子来说明:“可知平均速度的量值不一定等于平均速率”.对初中及高中物理老师来说,这是一个常见的题目,但是若要和小学数学“一贯”的话,就要再特别说明清楚:“这题的平均速率就是小学里的速度,而平均速度是位移除以时间,它的大小不能用来描述运动的快慢.”

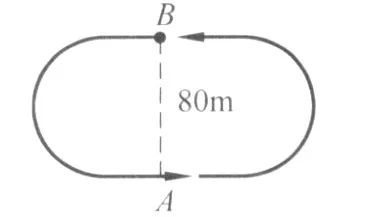
图2 操场问题

3 问题与讨论

3.1 日常生活用语和物理课本相矛盾

在中文里,我们惯用“速度”,而少用“速率”,而在英文的使用上,却是常用 speed而少用velocity.但物理课本里的速度是 velocity,速率却是speed.学术用语和日常用语的混淆,加上平均速度的定义又和生活经验相矛盾,这对学生的学习,不会造成困扰吗?

到底形容物体运动的快慢是速度还是速率?是 speed还是 velocity?在台湾,研究学童这个概念的论文,有的用速度,有的用速率,连英文的对应也有称 speed是速度,velocity是速率的.造成这样的混乱,恐怕和物理教科书的定义和日常生活习惯用语不一致脱不了关系.

3.2 瞬时与平均

不少课本都提到,瞬时速度简称为速度;瞬时速率简称为速率.我们日常生活中和课本里所提到的速度或速率,并不见得都是“瞬时”的意思吧?有些物理课本说,速度是向量,包括大小和方向,速度的大小就是速率,前述几个例子却都展现出速度的大小并不见得就是速率.还有,既然平均速度的定义与日常经验不符,物理课本为何要这样定义?物理课本里的定义,怎会有这么多的矛盾?

平均速度定义为位移除以时间并不奇怪,这样的定义是有意义的,是所举的例题把它弄奇怪了.平均速度 (位移除以时间)的定义应该用于时距很短的情况下,在时距很短很短的情况下,二点之间的路径长就趋近于位移,这是微积分里的非常非常重要的基本概念.因此,老师及教科书应该多举适当的例子让学生了解及体会,在时距很短的情况下,路径长会很接近位移,而不是故意举长时距长距离的例子 (如台北到花莲的自强号、上山下山问题)来强调路径长和位移的不同.

3.3 把运动分为三类

速度和速率的大小到底相不相同?如果我们把运动分为直线单向运动、一维往返运动和二维运动等三类来说明 (这是笔者自创的分法),问题就清楚多了.直线单向运动中,平均速度和平均速率的大小相等,瞬时速度的大小和瞬时速率也相等的,都只是有方向没方向的差别,因为大小都相等,所以教学上不适合用这样的例子来说明速度和速率的差别.一维往返运动 (如上山下山),只适合用来讲平均速率,若强调用这样的情况来计算平均速度,不仅不能帮助学生了解概念,反而造成如本文所讨论的各种矛盾与混淆.二维运动(如跑操场、秒针问题),适合结合极限的观念来说明在时间很短很短的情况下,瞬时速度的大小可以逼近瞬时速率.但若在长时间长距离的情况下,用来强调平均速度和平均速率的大小不等,笔者认为是不太恰当的.

3.4 瞬时速度的极限概念

瞬时速度的概念是物理上各种运动,如自由落体、抛体运动、圆周运动、简谐运动等的基础.牛顿当年就是基于要解决这些运动的数学问题,提出时间的无穷小变化量而发展出微积分的.

要了解平均速度和瞬时速度的概念,所举的例子应该是要让学生熟悉在什么情况下,位移和路径长很接近.其实这就是极限的观念,当年阿基米德计算圆周长就是用这样的想法 (如图3),三国时代的数学家刘徽描述得很贴切:“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体而无所失矣!”.

图3 以内接多边形估算圆周长的示意图

二维运动的例子是很适合用来教“极限”观念的.以前面秒针尖端点的例子来说,它的运动是等速率的,因此瞬时速度的大小就是平均速率,即圆周长 (2πr,r=10cm)除以绕一圈的时间 (60s),等于 1.0472(cm/s).我们所举的例子应该是让学生明了,秒针尖端从 11走到 12的位移的大小会比从 10走到 12更加接近它的路径长.如果计算的时间越短 (例如只算一秒),所得到的位移大小就越接近它的路径长,这样算出来的平均速度就越能代表瞬时速度.因此,笔者认为,使用得当的话,其实秒针问题是一个很好的例子.但是如果只考从 10走到 12的平均速度,反而会把平均速度的意义弄得很奇怪,对学生的学习不仅无帮助而且还有反效果.

瞬时速度的极限概念包括两个部分,一是长度的极限,二是时间的极限.如前所述,在二维运动的情况下,若一直切割下去,路径长就可以用位移大小来取代,这个概念并不是很难了解.学生比较难理解的恐怕是时间的极限部分,在微积分的发展上,这一个非零又很接近零的“无穷小量”概念,曾经造成了数学家们很大的困扰.因此,这可能是教学上学生较难理解的部分.所以,在中学的物理教学上,要如何避免直接教微积分,又能够让学生明了瞬时的极限观念,是一个值得大家深思的问题.

4 结论与建议

4.1 日常生活用语与教科书用语的不一致造成教学上的困扰

对英语体系的人来说,在日常生活中的 speed正好和物理上的 speed概念一致,velocity则是物理上专用的字,因此没有日常用语与教科书不一致的问题.对华文体系的人来说,教科书中 velocity和 speed分别被翻译成速度和速率,造成教科书用语和日常生活用语的不一致的现象:在日常生活中,我们惯用“速度”,而少用“速率”,但实际生活上遇到的例子大都是“平均速率”.于是,对教与学都造成了许多困扰.

4.2 过于强调位移和路径长的不同反而有效反果

平均速度的定义看来和日常生活相矛盾,并不是定义不对,而是我们所举的例题不恰当而把它弄奇怪了.平均速度是教瞬时速度概念的过渡,我们应该举例来帮助学生了解在“极限”的情况下位移大小和路径长很接近,而不是拿长时距长距离的例子来特别强调位移大小和路径长的不同.

[1] 王春奎,锺静.儿童速率概念之初探研究,师大学报,2004,49(1):41～64

[2] Chiu,Yun-Ju.A Study on the Misconceptions of Average Velocity from Teaching and Learning Approaches. Paper presented at the Conference of Asian Science Education(CASE2008),Kaohsiung,Taiwan,2008,February 20～23

MISCONCEPTIONS OF AVERAGE VELOCITY AND SPEED IN PHYSICS TEACHING

Chiu Yun-Ju
(General Education Center,Chang Gung University,Taiwan)

This paper addresses some factors which will make students confused in class when they are learning the definition of the average velocity.To teach the concept of average velocity,teachers must understand the mis match of daily language and textbook language will make students confused.Teachers must select suitable examples and strategies to help their students.

concepts;velocity;speed;kinematics;textbook

2011-03-05)

邱韵如 (1963年出生),女,台湾台北人,长庚大学通识中心助理教授,台湾师范大学物理博士,主要从事大一普通物理学、普物实验教学及科学教育研究.