工程机械液压泵和马达模型的非线性改进

王安麟,岳滨楠,周鹏举,刘 赫

(同济大学 机械工程学院, 上海201804)

工程机械产品当中行走液压传动的应用日趋广泛.在工程机械动力匹配问题方面, 液压泵和液压马达的效率对于工程车辆的性能影响不可忽视.通常液压件生产商为主机厂商提供试验测试得出的各工况的效率分布曲线供选用参考.然而,工程机械与其他采用液压传动的设备相比具有工况复杂、载荷变化剧烈的特点.传统的设计选型过程中,一般仅根据产品样本资料进行简易估计和静态匹配,无法进行动态量化模型计算, 因此工程机械行走液压传动系统在极端工况下容易出现匹配不合理的问题.为了实现合理的动力匹配, 解决厂商对于泵和马达最关心的各工况效率问题, 需进行工程机械的动力学建模, 其中液压泵和液压马达的模型必须能够描述不同工况下的效率变化, 以准确反映工程机械在不同工况下的性能.

大多数文献对于泵和马达的研究主要集中于斜盘动态特征的数学描述[1-3],但对于各工况效率的描述方面的研究较少.文献[4] 中提到了一些传统的效率计算模型, 但一般属于线性描述,且其中的系数没有较好的确定方法,应用较为困难.主流的键合图法建模[5]当中对于效率的处理方式是采用阻性元件分别表示机械摩擦和内泄漏反映其效率,但因液压元件具备复杂非线性特征, 这种线性建模方法面临参数确定困难和精度不足的问题.因此本文将集中研究精确描述效率的模型改进方法,建立优化算法,以优化并合理确定模型各参数, 使改进后模型能更精确地描述液压元件的特性.

1 传统模型的效率描述

对于泵和马达的模型, 目前主要采用键合图方法,键合图如图1 所示[5],转化为框图形式如图2 所示.图中,S f,Se分别为键合图理论中的流源和势源;0 ,1 分别为键合图理论中的共势结和共流结;TF为键合图理论中的变换器;m为变换器模数;R为阻性元件;Cf,Cv分别为摩擦系数和泄露系数;T i,ωi分别为机械端转轴的扭矩和转速;Po,Qo分别为液压端压力和流量;T f为机械摩擦力矩;QV为泄露流量.

图1 泵和马达的键合图模型Fig .1 Bond graph of pump and motor' s characteristic model

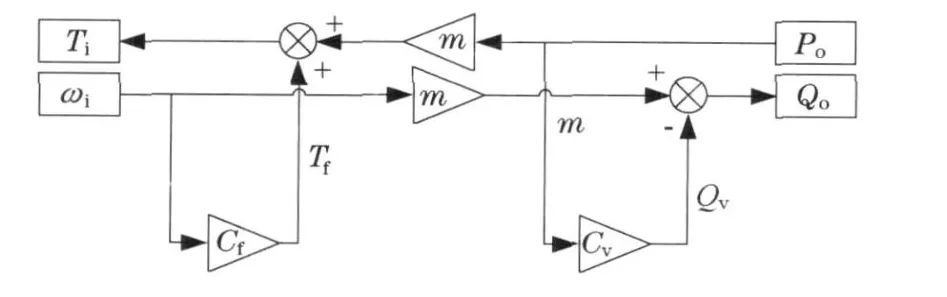
图2 泵和马达的模型框图Fig.2 Diagram of pump and motor' s model

因此, 模型主要参数为m及C f,Cv.其中变换器系数由泵的排量确定,以下列举阻性元件的方程式.机械摩擦力矩与转速关系为T f=ωi C f,内泄漏流量与工作压力关系为Qv=Po Cv.以上C f及C v属于需要确定的模型参数.

泵和马达的键合图中, 变换器两边的阻性元件可分别表示机械摩擦和内泄漏, 从而反映出其机械效率和容积效率在不同工况下的变化.根据机械摩擦与转速的关系以及内泄漏流量与工作压力的关系,可绘制出泵或马达产品各工况下效率分布图.

传统模型中阻性关系采用线性关系, 即机械摩擦力矩与转速成正比;内泄漏流量与工作压力成正比.因此如将其绘制为各工况下效率分布图的形式,则等效率曲线, 呈现为直线形式.而现有的泵和马达产品的样本效率图显示其等效率曲线, 呈现曲线形式.这说明实际的泵和马达具备非线性特性, 这使得线性模型在高压、低转速等极端工况下不够准确,只能适用于较小的工况范围内.

2 改进模型的提出

对传统键合图模型进行非线性改进, 采用平方关系代替一次关系, 即机械摩擦力矩与转速的平方成正比;内泄漏流量与工作压力的平方成正比;并在机械部分加入库伦摩擦力矩.对图2 中的框图进行改进, 如图3 所示.图中,Tf0为库伦摩擦力矩;Cf2,Cv2分别为二次摩擦系数和二次泄露系数.

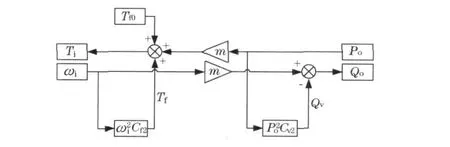
图3 泵和马达改进后模型框图Fig .3 Diagram of improved pump and motor' s model

机械摩擦力矩与转速关系为Tf=ω2iCf2;内泄漏流量与工作压力关系为Qv=P2oCv2.

加入库伦摩擦力矩Tf0,即认为初始力矩需要克服泵或马达内部的静摩擦启动工作, 在泵或马达正常工作阶段,Tf0也可作为模型动摩擦力的一部分.

式中:Ti为转轴力矩;T3为有效转化力矩;Tf0为库伦摩擦力矩.

可见改进后模型需要确定的参数为Cf2,Cv2及Tf0.

因平方关系可使得等效率曲线具备圆弧曲线形式,同时考虑了启动所需的摩擦力矩,因此改进后的模型应比原始线性模型更加符合实际情况.以下将对2 种模型进行对比.

3 改进模型与传统模型的对比分析

3 .1 参数确定优化算法的提出

在实际工程应用中, 模型中参数确定是难点.因种种原因, 厂商通常不能提供键合图模型中所需的参数Cf及Cv.但模型的参数变化与各工况下泵和马达的效率有关, 通常厂商可提供实验得出的全工况效率分布图,以Sauer-Danfoss 的51 型柱塞马达为例, 其效率分布图如图4[4].

图4 Sauer-Danfoss 51 系列柱塞马达的等效率曲线分布Fig .4 Distribution of Sauer-Danfoss 51 series piston motor' s equal efficiency curve

模型中参数Cf及Cv与机械效率和容积效率相关,而这两者的乘积即为总效率, 所以模型中参数与总效率的分布有关.厂商提供的效率分布图为实验台测试得出,可作为试验数据来评价模型的精确性.因此提出以下方法:以样本效率分布图中的实验数据为评价基准, 效验不同模型参数下各工况的计算理论效率值,并优化模型参数,使得模型在各工况下计算得出效率的误差最小化.优化程序如图5 所示.

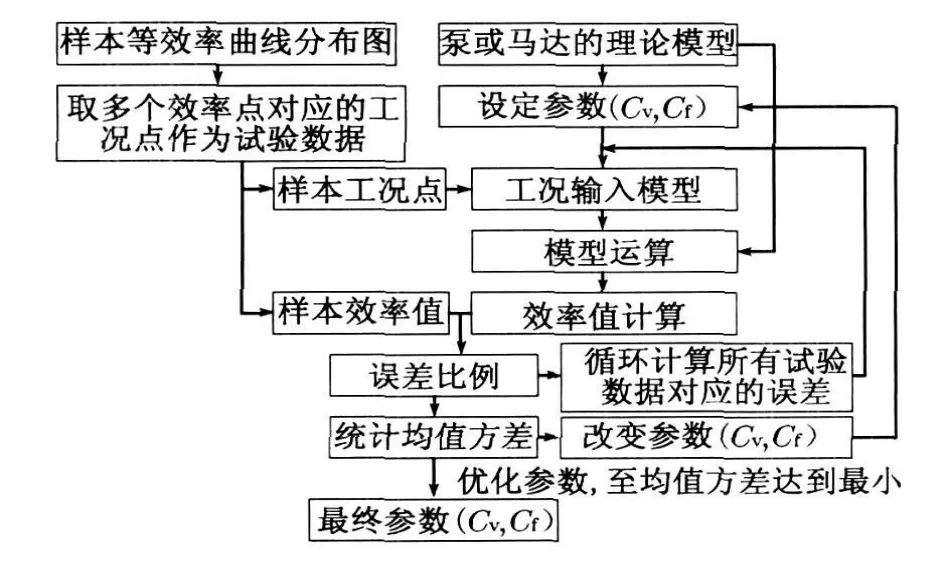
图5 模型参数优化流程Fig .5 Optimization process of models' parameters

也可选取Cf2,Cv2及Tf0为优化参数,如此不仅可根据样本数据确定参数Cf及Cv,也可解决新模型的参数Cf2,Cv2及Tf0的确定问题.

为与产品样本进行科学的对比, 必须对2 种模型的参数均进行优化, 分别得出其与实际情况最为符合的参数设定,再进行误差的分析对比[6-7].以下模型对比过程中将首先采用优化程序对2 种模型的参数进行优化.

3.2 2 种模型的对比

以一种典型产品对象为例对2 种模型进行对比, 以证明改进模型的优越性.这里以Sauer-Danfoss 的51 系列110 柱塞马达为例,产品参数如表1 所示[4].

表1 Sauer-Danfoss 51 系列110 型柱塞马达参数Tab.1 Parameters of Sauer-Danfoss 51 series 110 piston motor

为优化模型参数,以效率分布图(图4)中的等效率曲线上的点作为试验采样点作为以下分析中优化的试验数据依据.取点越密集则优化结果越精细,本示例中共取了137 个点进行计算, 其中74 .5 %效率曲线上取29 个点, 84 .5 %效率曲线取32 个点,90 .5 %效率曲线取30 个点, 93 .5 %效率曲线取30个点, 94 .5 %效率曲线取16 个点.

对比将采用如下步骤进行:①采用优化程序优化模型参数;②根据优化后参数绘制效率分布图;③根据样本的数据分析其误差比例分布;④计算误差比例统计数据.根据以上分析结果, 即可量化反应改进后模型在精度方面的提高.

3 .2.1 模型参数优化

针对2 种模型, 根据样本的实验数据与模型计算数据进行对比, 建立运算程序优化摩擦系数和内泄系数2 个参数使效率的均值和方差达到最小.对2种模型分别进行优化参数, 得到的参数优化结果如表2 所示.

表2 2 种模型参数优化结果Tab.2 Optimization results of two models' parameters

3 .2.2 等效率曲线图对比

根据以上参数, 可分别计算不同工况的效率值,绘制效率分布图如图6 所示.

从图6 中可以看到,传统模型的等效率线呈直线形态,与图4 相似性很低, 这是由模型的线性特征决定的.而改进后模型的等效率线与图4 对比具有明显的相似性, 可见改进模型的描述更加精确.为量化说明问题, 以下将对2 种模型的误差进行分析.

3 .2.3 误差比例分布对比

对样本中实验数据的效率值与模型计算的效率值进行对比,并分别绘制2 种模型的误差比例分布,如图7 所示.

实际工作的极端工况中, 泵或马达的最大功率相对稳定, 当液压端压力呈现高压力时,转速呈现为低转速,而当液压端转速呈现高转速时,压力呈现为低压, 因此泵或马达的产品极端工况表现为高压力、低转速工况和低压力、高转速工况.根据工程实际应用,厂方提供的产品效率分布图通常只表述高压力、低转速工况,如0～30 %转速工况.

图6 2 种模型的等效率曲线理论分布Fig .6 Theoretical distribution of two models' equal efficiency curve

图7 2 种模型的误差比例在各转速工况的分布Fig.7 Distribution of two models' tolerance proportion in various speeds

由图7 可见,传统模型在高转速区段误差较小,但在高压力、低转速(0～30 %)的极端工况下误差较大,而改进后模型在这些极端工况下误差明显减小.这说明改进后模型的工况适用范围较好, 在较复杂工况的设备建模中更能体现优势.

3.2.4 误差比例统计

将图7 中数据进行统计分析, 得到2 种模型的误差比例均值和方差如表3 所示.

表3 2 种模型的误差比例统计Tab.3 Statistic of two models' tolerance proportions

统计显示改进后模型的误差均值和方差都更小,说明模型精度在整体上得到了提升.

3.2.5 结果讨论

根据以上模型对比分析, 可得出以下结论:

(1)模型得出的工况效率分布图(图6)与实验图线(图4)对比表明, 改进后模型明显比传统模型具备更好的相似性.

(2)误差比例分布表明, 传统模型在高压、低转速等极端工况下误差较大,而新模型的误差则较小.

(3)与试验数据对比误差分析证明, 传统模型误差均值比例为3 .55 %, 方差比例为0 .005 298 0 ;改进后模型误差均值比例为1 .18 %, 方差比例为0 .000 487 5 ,可见改进后模型精度得到了提升.

此外, 已有的一些其他泵和马达产品样本的效率分布图显示, 等效率曲线形态与本文中的Sauer51型马达的等效率曲线形态具备相似性, 因此, 虽然本文尚未对其他厂或其他型号的泵和马达应用本模型进行研究, 但泵和马达的键合图模型在结构上具备一定的普适性, 区别在于模型的各参数数值不同以及模型描述产品的准确度有所差别.只要通过采用优化程序进行参数调节,本模型均可实现对其较为准确的描述.但鉴于实际问题的复杂性,模型的适用性仍然需要更进一步的研究.

4 结论

与传统模型相比,改进后模型得出的工况效率分布图与实验图线明显具备更好的相似性.与试验数据对比误差分析证明, 传统模型误差均值比例为3 .55 %,方差比例为0 .005 298 0 ;改进后模型误差均值比例为1 .18 %,方差比例为0 .000 487 5 ,可见改进后模型精度得到了提升.

[1] Zhang X, Cho J, Nair S S, et al.Reduced order modeling of the dynamics of an indexing valve plate pump[C] ∥Proceedings of the American Control Conference.Chicago:[s.n.],2000:3595-3599.

[2] Manring Noah D.T he control and containment forces on the swash plate of an axial piston pump utilizing a secondary swashplate angle [C] ∥Proceedings of the American Control Conference.Anchorage:[s .n.],2002:4837-4842.

[3] DU Hongliu.Pressure control with power limitation for hydraulic variable displacement piston pumps[C] ∥Proceedings of the American Control Conference. Anchorage:[s.n.],2002:940-945.

[4] 姚怀新.工程车辆液压动力学与控制原理[M] .北京:人民交通出版社, 2006.YAO Huaixin.Hydraulic dynamics and control principles of engineering machinery [M] .Beijing:China Communications Press, 2006.

[5] 王中双.键合图理论及其在系统动力学中的应用[M] .哈尔滨:哈尔滨工程大学出版社, 2007.WANG Zhongshuang.Bond graph theory and its application in system dynamics[M] .Harbin:Harbin Engineering University Press, 2007.

[6] 李晓田, 王安麟, 慈健.变冲击系数的几何参数化变矩器特性模型[J] .农业机械学报, 2009(7):15.LI Xiaotian, WANG Anlin, CI Jian.Parametric torque converter dynamic model with variable shock loss coefficient [J] .Transactions of the Chinese Society for Agricultural Machinery,2009(7):15.

[7] 李晓田, 王安麟, 慈健, 等.基于参数敏感度分析的管片散热器再设计方法[J] .同济大学学报:自然科学版, 2009(10):1498.LI Xiaotian, WANG Anlin, CI Jian, et al.Aredesign method based on parameter-sensitivity analysis for plate fin-and-tube radiators[J] .Journal of Tongji University:Natural Science, 2009(10):1498.