不含相邻三角形的平面图的线性 2-荫度*
盛慧玉
(浙江师范大学数理与信息工程学院,浙江金华 321004)
0 引 言
本文仅考虑简单有限无向图.对于一个图 G,分别用 V(G),E(G),Δ(G),δ(G)表示点集、边集、最大度和最小度.k-点表示度是 k的顶点,k+-点表示度至少是 k的顶点.「x┒表示不小于实数 x的最小整数,┖x」表示不大于实数 x的最大整数.一个图 G的边划分是指将 G分解成子图 G1,G2,…,Gm,使得E(G)=E(G1)∪E(G2)∪…∪E(Gm)且 E(Gi)∩E(Gj)=Ø(i≠j);线性 k-森林是指一个图 G,它的每个连通分支是长至多为 k的路;图 G的线性 k-荫度是指使得 G可以边划分成 m个线性 k-森林的最小整数m,用 lak(G)表示.显然,当 k≥1时,lak(G)≥lak+1(G).特别地,la1(G)就是 G的通常边色数χ′(G);la∞(G)表示每个分支路均为无限长的情况,也就是 G的线性荫度 la(G).
图的线性 k-荫度最早由 Habib和 Péroche引进,文献 [1-3]对此作了深入的研究;圈、树、完全图及完全二部图的线性 2-荫度在文献 [1,4]中进行了讨论;文献 [5]证明了当 k≥5时,对于 3-正则图 G有lak(G)≤2,而且该结果是最好的.关于线性荫度的一个著名猜想由 Akiyama[6]提出:对于每一个简单图面图,文献[10-11]证明了该猜想成立.

1 几个引理
引理 1 设 G是不含相邻三角形且δ(G)≥2的平面图,则以下 2个结论中必有 1个成立:存在边xy∈E(G),使得 dG(x)+dG(y)≤11;存在 2-交错圈 v1v2…v2sv1,使得 d(v1)=d(v3)=…=d(v2s-1)=2.
证明 假设均不成立,则以下断言成立:
断言 1 ∀xy∈E(G),满足 dG(x)+dG(y)≥12,从而 2-点的邻点一定是 10+-点,3-点的邻点一定是9+-点.
断言 2 设 G2是 G中 2-点关联的边生成的子图,则 G2是森林.
由假设不成立可知,G2不含偶圈,由断言 1知,G中任意 2个 2-点不相邻,从而 G2中也不含奇圈,所以 G2是森林.
断言 3 G2包含一个匹配M,使得M饱含 G中的所有 2-点.

假设 G中的顶点和面已被赋权,即当 x∈V(G)∪E(G)时,初始权 ch(x)=d(x)-4,ch*(x)表示最终权.
权转移规则如下 (见图 1):
R1:每个 2-点从 2-master得权 2.

3)若 3-面关联均为 5+-点,则 3个点分别
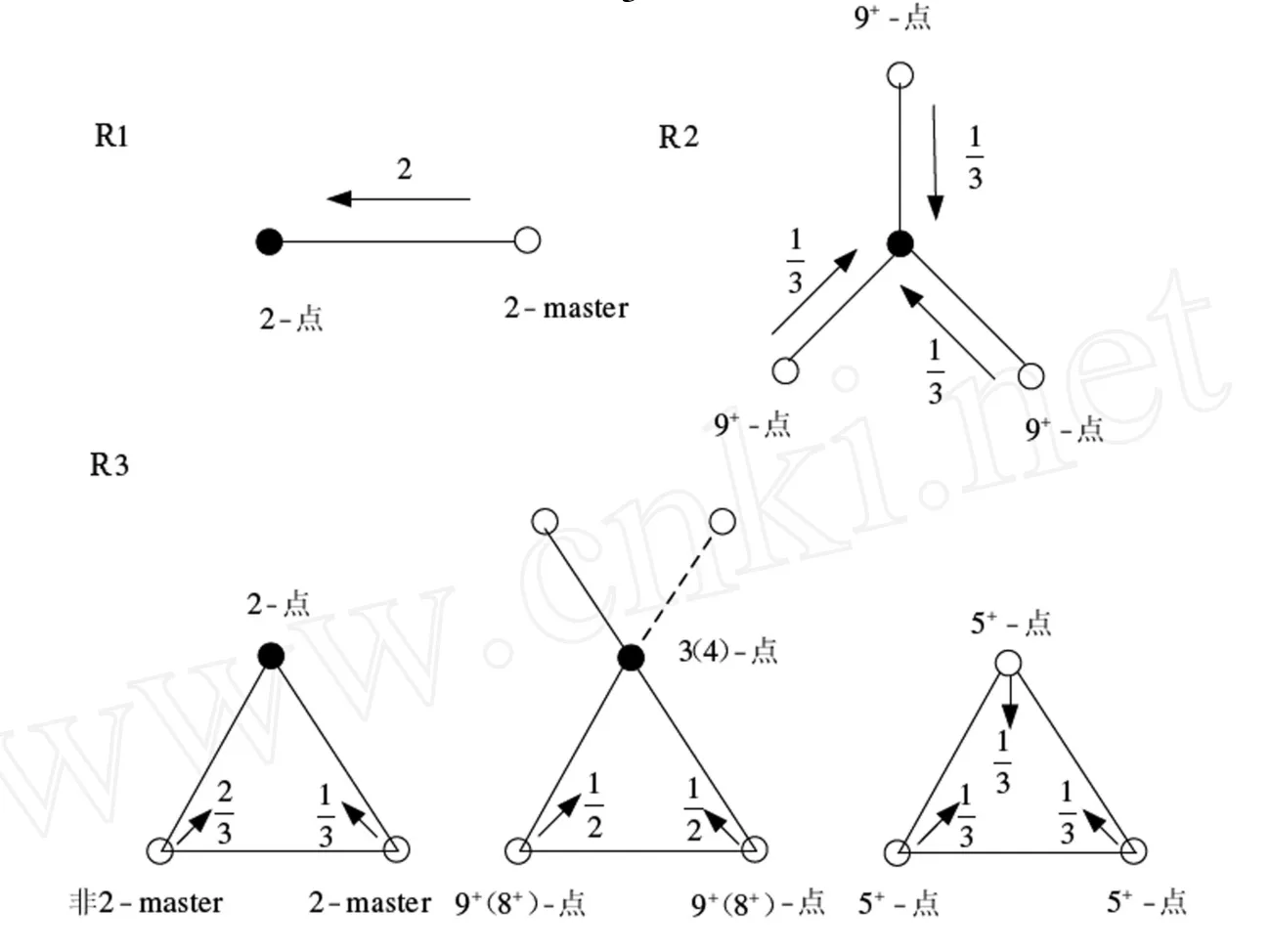
图 1 权转移规则
验证新权:
下面通过 2个断言证明∀x∈V∪F,有 ch*(x)≥0.
断言 4 ∀f∈F(G),ch*(f)≥0.
当 f是 3-面时,根据 R3,可以接受其相关联的 2个或 3个点的权共 1,则 ch*(f)≥0.
当 f是 4+-面时,f既不接受权,也不转出权,故 ch*(f)=ch(f)≥0.
断言 5 ∀v∈V(G),ch*(v)≥0.
当 v是 2-点时,根据 R1,它的 2-master给它权 2,故 ch*(v)=-2+2=0.

当 v是 10+-点时,分 2种情况讨论:


证明 对 |V(G)|+|E(G)|用数学归纳法.当 |V(G)|+|E(G)|≤5时,结论显然成立.当 |V(G)|+|E(G)|≥6且Δ(G)≤6时,只要令 F1=F2=Ø,H=G即满足引理 2条件.

如果δ(G)≥2,由引理 1,只需考虑 2种情况.
1)存在边 xy∈E(G),使得 dG(x)+dG(y)≤11.


2 主要结果
证明
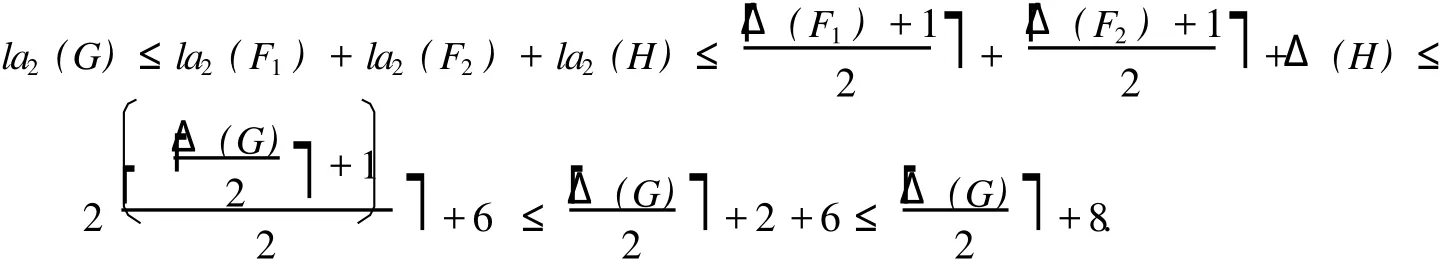
定理 1证毕.
[1]Aldred R E L,Wormald N C.More on the lineark-arboricity of regular graphs[J].Australas J Comb,1998,18(1):97-104.
[2]Be rmond J C,Fouquet J L,HabibM,et al.On lineark-arboricity[J].DiscreteMath,1984,52(2/3):123-232.
[3]Jackson B,Wormald N C.On the lineark-arboricity of cubic graphs[J].DiscreteMath,1996,162(1/2/3):293-297.
[4]HabibM,Pèroche P.Some problems about linear arboricity[J].DiscreteMath,1982,41(2):219-220.
[5]Thomassen C.Two-coloring the edges of a cubic graph such that each monochromatic component is a path of length at most 5[J].J Comb Theroy Ser:B,1999,75(1):100-109.
[6]Akiyama J.Three developing topics in graph theory[D].Tokyo:University of Tokyo,1980.
[7]Akiyama J,Exoo G,Harary F.Covering and packing in graphsⅢ:Cyclic and acyclic invariants[J].Math Slovaca,1980,30(4):405-417.
[8]Enomoto H,Pèerche B.The linear arboricity of some regular graphs[J].J Graph Theory,1984,8(2):309-324.
[9]Guldan F.The linear arboricity of 10-regular graphs[J].Math Slovaca,1986,36(3):225-228.
[10]Wu Jianliang.On the linear arboricity of planar graphs[J].J Graph Theory,1999,31(2):129-134.
[11]Wu Jianliang,Wu Yuwen.The linear arboricityofplanar graphsofmaximum degree seven is four[J].J Graph Theory,2008,58(3):210-220.
[12]Lik KW,TongLida,WangWeifan.The linear 2-arboricity of planar graphs[J].Graphs Comb,2003,19(2):241-248.
[13]孙向勇,吴建良.特殊平面图的线性二荫度[J].山东师范大学学报:自然科学版,2007,22(3):9-13.
[14]Chen B L,Fu H L,Huang K C.Decomposing graphs into forests of pathswith size less than three[J].Australas J Comb,1991,3(1):55-73.
(责任编辑 陶立方)

