退火工艺对 Fe基薄带纵向＊驱动应力阻抗效应的影响

李文忠, 郑建龙, 马 云, 何 佳, 方允樟

(浙江师范大学数理与信息工程学院,浙江金华 321004)

0 引 言

1997年,Shen等[1]首次在负磁致伸缩系数的 CoSiB非晶丝中发现了巨应力阻抗 (GSI)效应,其应力阻抗比可达 20%,是半导体力敏材料的 6倍以上,此后一直受到各国研究者的关注.但是,由于不断发展的实际应用需求[2-3],人们仍然追求更高灵敏的应力传感器.为了提高巨应力阻抗的灵敏度,研究者做了大量的工作:文献[4]通过对 Fe73.5Cu1Nb3Si13.5B9合金掺 V进行组分调制获得巨应力阻抗比达-22.4%;文献[5]通过对 Fe73.5Cu1Nb3Si13.5B9合金薄带进行温度退火处理使应力阻抗比达 25%;文献[6]又通过对 Fe73.5Cu1Nb3Si13.5B9合金薄带外加张应力电流退火来改善纳米晶的磁导率和磁各向异性,获得的应力阻抗比高达 350%,是目前所见报道中采用横向驱动模式获得的最大值,显著提高了应力阻抗效应的灵敏度.

1998年,杨介信等[7]在研究 Fe73.5Cu1Nb3Si13.5B9合金薄带的巨磁阻抗效应 (G M I)时采用了纵向驱动的方法将磁阻抗的灵敏度提高了 1个数量级,由于这种方法采用非接触模式[8],可以有效地避免横向驱动模式中导线与晶带之间的接触电阻及由此产生的焦耳热损耗,同时产生了一个沿晶带纵向的磁化场,从而影响材料内部的磁化状态,导致其产生较大的磁阻抗效应.这种方法用于应力阻抗效应 (SI)应该能够获得更高的灵敏度,但相关工作至今仍未见报道.

本研究采用了纵向驱动的方法对 Fe73.5Cu1Nb3Si13.5B9合金薄带的应力阻抗效应进行了系统研究,发现其在纳米微晶状态下的应力阻抗比可达 650%,应力响应灵敏度达 120%/MPa.这种获得高灵敏的应力阻抗效应的方法为研发高灵敏的新型应力传感器提供了一种新途径.

图 1 纵向驱动应力阻抗效应测量系统简化图

1 实 验

采用单辊快淬的方法制备了宽为 0.4 mm,厚为30μm,成分为 Fe73.5Cu1Nb3Si13.5B9的非晶薄带.截取长 20 mm的样品在空气中分别以 400,500,550,580,620℃退火,保温 1 h后自然冷却到室温,退火过程中样品的长度方向与地磁场平行.用DSC对 Fe基合金薄带进行了热分析,用 XRD(Cu-kα)对 Fe基合金薄带进行了结构的分析.在应力阻抗测量过程中,样品被放置在一个直径为 0.57 mm的驱动线圈内,组成一个等效的阻抗元件,接入 HP4294A型阻抗分析仪进行应力阻抗测试,线圈内通过 10 mA的交流驱动电流,在样品的纵向产生一个驱动磁化场,驱动频率从 40 Hz到 20 MHz.图 1为纵向驱动应力阻抗测量系统简化图,样品纵向加载的应力范围为 0～105 MPa,所加载的应力由外加不同砝码提供.定义应力阻抗比为

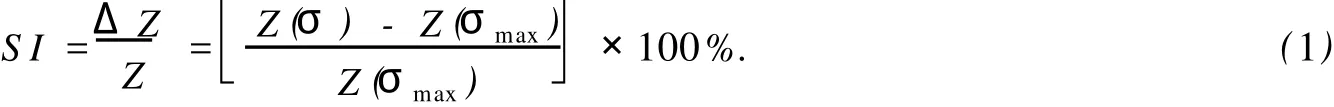
式 (1)中,Z(σ)和 Z(σmax)分别表示在任意外加张应力和最大张应力时的阻抗值.定义应力阻抗的灵敏度为

式 (2)中:(ΔZ/Z)max为最大应力阻抗比;ΔH为应力阻抗比曲线的半高宽.

2 结果与讨论

2.1 Fe基合金薄带的 XRD分析

图 2 不同温度退火后 Fe基合金薄带的 XRD谱图

为了说明温度退火后 Fe基合金薄带微结构对 SI效应的影响,图 2为 Fe基合金薄带在不同温度退火 1 h后的 XRD衍射图谱,其中铸态和 400℃之前退火样品的 XRD图谱呈现为典型的“馒头峰”,表明400℃之前退火的样品仍为非晶态.这个过程对合金薄带样品来说是个内应力释放的过程,SI比铸态有明显的提高.当退火温度达到 500℃时,在 (110),(200)和 (211)面开始出现了α-Fe(Si)晶化峰,SI效应得到了进一步的升高.当退火温度达到 550℃时,合金薄带样品内的 (110)面α-Fe(Si)晶化峰得到进一步 增 强,由 Scherrer公 式[9]D =0.96λ/(Bcosθ)(其中:λ是 X射线的波长;θ是衍射角;B为衍射峰的半高宽)计算得,退火温度从 500～620℃的α-Fe(Si)纳米晶粒尺寸为 10～15 nm,晶粒尺寸变化不大,此时样品的矫顽力达到最低值,磁导率达到一个峰值,而磁导率直接影响材料的磁阻抗[10]及应力阻抗效应[11].由图 2可知,退火温度在550℃时具有最显著的 SI效应.笔者认为当退火温度达到 550℃时,α-Fe(Si)纳米晶相和非晶相存在着较强的磁交换耦合作用,局域的磁晶各向异性平均化,导致其磁导率提高,进而使 SI效应得到改善.当退火温度为580℃时,α-Fe(Si)晶化峰更加“尖锐”,纳米晶相所占的体积分数进一步地增大,SI效应逐渐减弱.当退火温度在 620℃以上时,晶化进一步加强并伴随有硬磁相 Fe2B和 Fe3B的出现,导致磁导率的急剧下降,应力阻抗效应极其微弱,SI值几乎接近于零.以上结果表明,退火过程中 Fe基合金薄带微结构的变化对纵向驱动 SI效应有明显的影响.

2.2 不同温度退火 Fe基合金薄带的 SI效应

图 3为 Fe基合金薄带在不同温度退火处理后的纵向驱动应力阻抗效应曲线.图 3中,(a),(b),(c),(d)分别代表 Fe基合金薄带在铸态及经 500,550,580℃退火 1 h后在驱动频率为 2.375MHz时的纵向驱动应力阻抗效应曲线.

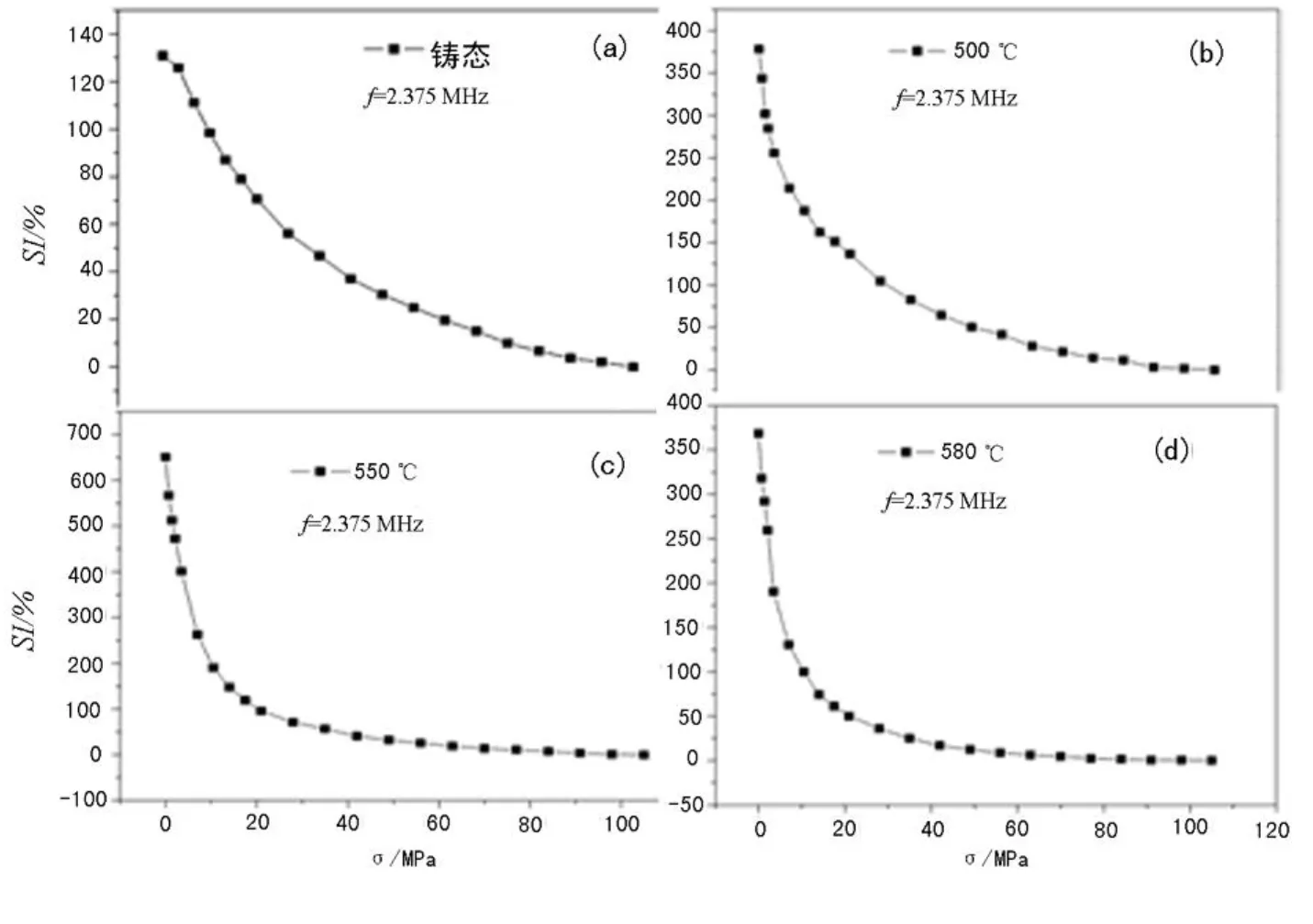
图 3 Fe基合金薄带 SI曲线

数据显示样品在铸态下应力阻抗比较小,随应力的增加单调递减.当退火温度为 500℃时,由于样品开始有纳米晶粒析出,软磁性能得到改善,因而应力阻抗比随之有明显升高.当退火温度达到550℃时,非均质的纳米晶粒逐渐增多,并与样品内部的残余非晶相达到一定的比例,此时样品的综合软磁性能达到最佳,应力阻抗比也达到最大值 650%.当外加应力逐渐增加时应力阻抗比呈单调递减,这是由于纵向驱动的磁化场与样品的易磁化方向一致.当外加张应力时,样品畴壁的移动和磁矩的转动受到阻碍,从而导致了有效磁导率的下降,进而导致了应力阻抗值的下降.当退火温度继续升高达到 580℃时,样品中的α-Fe(Si)相纳米晶粒逐渐长大,同时纳米晶粒所占的比例进一步增大,导致了有效磁导率的下降,从而使得应力阻抗比下降.

磁弹性材料的磁致伸缩系数对材料的 SI效应有很大的影响,早期 Twarowski等[12]在研究Fe73.5Cu1Nb3Si13.5B9合金在退火过程饱和磁致伸缩系数的变化时证实:非晶具有较大的正磁致伸缩系数,而α-Fe(Si)纳米晶具有负的磁致伸缩系数,当非晶相与纳米晶相达到一定的比例时,饱和磁致伸缩系数趋于零.由图 3可知,在纵向驱动模式下,非晶和纳米晶样品的 SI曲线都表现为随外应力的增加而单调下降,这是因为:具有正磁致伸缩系数的材料受到张应力时,由于磁化方向和张应力方向一致,其外加应力相当于一个等效的磁场,由于磁弹耦合作用,薄带内部的等效场发生改变,从而影响自发磁化,进而影响有效磁导率,最终导致非晶和纳米晶状态下纵向驱动 SI曲线随外应力的增加而单调降低.同时,比较非晶和纳米晶状态的 SI曲线,明显看到纳米晶时 SI曲线随应力下降的趋势比较快,在较小的应力范围内就达到饱和,这是由于对于正磁致伸缩系数材料而言,当样品受到张应力时,由于磁化方向和张应力方向一致,其外加应力相当于一个等效的磁场,由于非晶态样品的磁致伸缩系数比较大,当施加一个较大的张应力时可以等效为施加一个比较小的外磁场.因此,铸态 Fe基合金薄带的 SI曲线随应力的下降趋势比较缓慢.与此相反,纳米晶样品的磁致伸缩系数比较小,样品轴向施加一较小的应力时可以等效为施加了一个比较大的磁场,因而其 SI曲线随应力的下降趋势比较快,在较小的应力范围内就达到饱和,应力响应灵敏度较高.

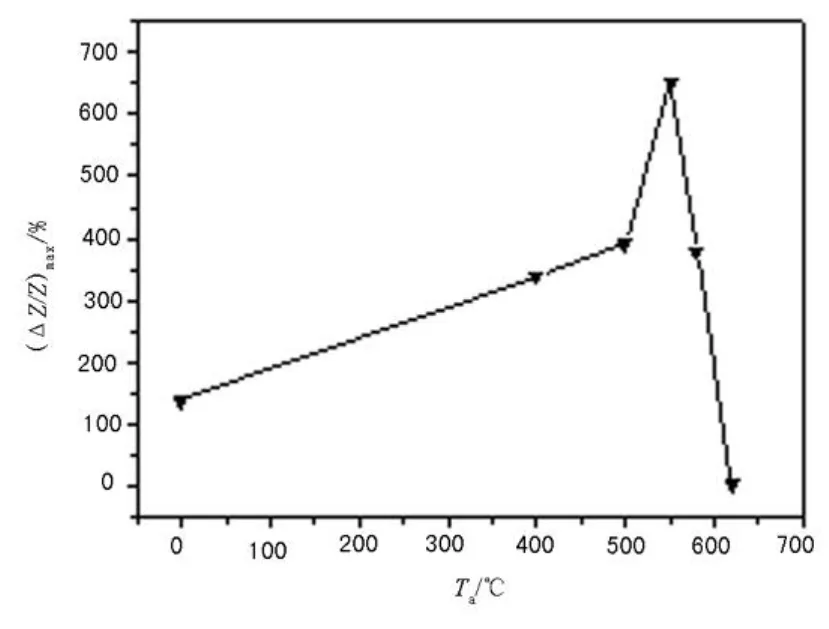
图 4 最大应力阻抗比与退火温度的关系

为了说明退火温度对 Fe基合金薄带 SI的影响,图 4显示 Fe基合金薄带样品在铸态和经 400,500,550,580,620℃退火 1 h的最大应力阻抗比随退火温度的变化关系.开始时应力阻抗比随退火温度的升高而增大,当退火温度达到 550℃时,应力阻抗比达到最大值,之后随着退火温度的升高应力阻抗比随之下降.上述结果表明:样品在退火过程中纳米晶的生长对材料纵向磁结构有很大的影响,同时材料的综合软磁性能与纵向驱动应力阻抗效应有密切的关系.

2.3 Fe基合金薄带 SI效应与频率的关系

图 5 Fe纳米晶薄带应力灵敏度随频率变化关系

通常认为 SI效应与材料的磁导率、磁致伸缩系数以及磁趋肤深度有关,当磁弹性材料受到张应力作用时,材料发生相应的应变.由于磁弹耦合的作用,材料内部的等效磁场发生改变,从而影响自发磁化,导致了磁导率的改变,同时由于驱动频率的变化,进而影响趋肤深度δ=磁导率)的变化,最终影响到 SI效应的改变.图 5为Fe73.5Cu1Nb3Si13.5B9合金薄带在 550℃退火纳米晶状态下应力响应灵敏度随频率的变化关系.应力响应灵敏度ξ由方程 (2)计算可得.开始时由于趋肤效应不明显,应力响应灵敏度随频率的增加而增加,在驱动频率f=2.375 MHz时应力响应灵敏度达到最大值ξ=120%/MPa,并随频率的进一步增大而快速降低.在频率 f≤2.375 MHz时,应力响应灵敏度随频率迅速增加,可能是由于 Fe基纳米晶薄带畴壁的移动和磁矩的转动,从而导致应力阻抗增加的幅度大于其应力各向异性的增加.相反,当驱动频率 f≥2.375MHz时,由于趋肤效应抑制着畴壁的移动,SI效应主要由旋转磁化引起,应力阻抗的降低并伴随着应力各向异性的增加,从而导致灵敏度的快速下降.

3 结 论

采用纵向驱动模式可以获得较横向驱动模式更为显著的 SI效应,这为研发高灵敏的应力传感器提供了一种新途径.退火温度可以明显地改善 Fe基合金薄带的 SI效应.经 550℃退火 1 h的样品,在驱动频率为 2.375 MHz时,应力阻抗比和应力响应灵敏度分别达到最大值 650%和 120%/MPa,可能是由于退火过程中内应力的释放以及非晶和纳米晶达到一定比例后两者特殊的磁弹耦合作用所致.

[1]Shen L P,Uchiyama T,Mohri K,et al.Sensitive stress-impedance micro sensor using amorphous magmetostritive wire[J].IEEE TransMagn,1997,33(5):3355-3357.

[2]Mohri K,Uchiyama T,ShenL P,et al.Amorphouswire and CMOS IC-based sensitive micro-magnetic sensors(M I sensor and SI sensor)for intelligentmeasurements and controls[J].J MagnMagnMater,2002,249(1/2):351-356.

[3]Kusumoto D,ShenL P,Naruse Y,et al.Detection of finger-tip blood vesselpulsation usingCoSiB thin amouphouswire CMOS-I C SI sensor[J].IEEE TransMagn,1999,35(5):4115-4117.

[4]Hu Jifan,Qin Hongwei,Chen Juan,et al.Giant stress-impedance effect in Fe73.5CuNb3-xVxSi13.5B9amorphous ribbons[J].JMagnMagnMater,2003,266(3):290-295.

[5]LiDeren,Lu Zhichao,Zhou Shaoxiong.Giant stress-impedance effect in amorphous and thermally annealed Fe73.5Cu1Nb3Si13.5B9ribbons[J].SensActuatorsA,2003,109(1/2):68-71.

[6]LiD R,Lu Z C,Zhou S X.Magnetic anisotropy and stress-impedance effect in Joule heated Fe73.5Cu1Nb3Si13.5B9ribbons[J].J Appl Phys,2004,95(1):204-207.

[7]杨介信,杨燮龙,陈国,等.一种新型的纵向驱动巨磁致阻抗效应[J].科学通报,1998,43(10):1051-1053.

[8]Wang Z C,Gong F F,Yang X L,et al.Longitudinally driven giantmagnetoimpedance effect in stress-annealed Fe-based nanocrystalline ribbons[J].J Appl Phys,2000,87(9):4819-4821.

[9]CullityB D.Element of X-ray diffraction[M].2nd ed.Reading,Mass:Addison-Wesley,1978:102.

[10]PhanM H,Peng H X,W isnomM R,et al.Effectof annealingon the microstructure andmagnetic propertiesof Fe-based nanocompositematerials[J].Composites:PartA,2006,37(2):191-196.

[11]BayriN,Atalay S.Giant stress-impedance effect in Fe71Cr7Si9B13amorphouswires[J].Journal ofAlloys and Compounds,2004,381(1/2):245-249.

[12]Twarowski K,KuimiiiskiM,Siawska-Waniewsha A,et al.Magnetostriction and its temperature dependence in FeCuNbSiB nanocrystalline alloy[J].J MagnMagnMater,1995,150(1/2):85-92.