关于弱d-Koszul模的一个注记＊

陈沛森

(1．浙江师范大学数理与信息工程学院，浙江 金华 321004;2．义乌工商职业技术学院，浙江 义乌322000)

Koszul代数最初由Priddy［1］于1970年提出，它是一类具有许多优美同调性质且在数学的诸多分支均有重要应用的二次代数．受整体维数是3的Artin-Schelter正则代数的影响，Berger［2］于2001年首次把这类代数推广到高阶齐次分次代数的情形，引入了非二次的Koszul代数;Green等［3］又把这类代数进一步地推广到0次分支是半单的情形，并称这类代数为d-Koszul代数;2003年，Martínez-Villa等［4］研究了Koszul代数上有限生成分次模的Koszul性质，定义了弱Koszul模的概念;2007年，作为弱Koszul模和d-Koszul模的推广，吕家凤等［5］研究了d-Koszul代数上有限生成分次模的d-Koszul性质，引入了弱d-Koszul模的概念．特别地，文献［5］的主要结果之一是证明了每个弱d-Koszul模都可以由d-Koszul子模来逼近．在证明该结果时，下面这个结果发挥了重要作用:

命题1［5］设A是d-Koszul代数，0→K→M→N→0是有限生成的分次A-模正合列，则

1)如果K和M是弱d-Koszul模且JkK=K∩JkM，k≥0，则N是弱d-Koszul模;

2)如果K和N是弱d-Koszul模且JK=K∩JM，则M是个弱d-Koszul模．

从命题1可以看出，弱d-Koszul模范畴在一定的条件下是扩张封闭的且保持单同态的余核．一个自然的问题是:弱d-Koszul模范畴在什么情形下保持满同态的核?本文的主要目的就是给出一个使得弱d-Koszul模范畴在满同态的核下封闭的充分条件．

定理1 设A是d-Koszul代数，0→K→M→N→0是有限生成的分次A-模正合列且M和N是弱d-Koszul模．若对任意的 i，k≥0，有 JkΩi(K)=Ωi(K)∩JkΩi(M)，则 K 也是弱 d-Koszul模．其中:J是 A的分次Jacobson根;Ωi表示第i个合冲．

为了证明定理1，先给出2个引理．

引理1［5］设0→K→M→N→0为gr(A)中的正合列，则下列命题等价:

1)JkK=K∩JkM，k≥0;

2)A/Jk⊗AK→A/Jk⊗AM(k≥0)是单同态的;

3)0→JkK→JkM→JkN→0(k≥0)是正合的;

4)0→JkK/Jk+1K→JkM/Jk+1M→JkN/Jk+1N→0(k≥0)是正合的;

5)0→JkK/JmK→JkM/JmM→JkN/JmN→0，m ＞k≥0．

引理2 设A是分次代数，0→K→M→N→0是有限生成的分次A-模正合列，则JK=K∩JM当且仅当有如图1所示的行列正合的交换图．

图1 正合交换图之一

图1 中，P0→K→0，L0→M→0及Q0→N→0是分次投射盖．

证明 必要性 由题设JK=K∩JM，再根据引理1，可得正合列0→K/JK→M/JM→N/JN→0．注意到对任意有限生成的A-模M，A⊗A0M/JM→M→0是分次投射盖．现令

因为A0是半单的，故可得正合列0→P0→L0→Q0→0．于是，可得如图2所示的除顶行外的行列正合的交换图．

图2 正合交换图之二

根据“3×3”引理，可得正合列0→Ω1(K)→Ω1(M)→Ω1(N)→0，故必要性得证．

充分性 注意到一个有限生成的分次模的分次投射盖在同构意义下是唯一的，故不妨设P0:=A⊗A0K/JK，L0:=A⊗A0M/JM，Q0:=A⊗A0N/JN．由图1的中间一行是正合的可得正合列0→A⊗A0K/JK→A⊗A0M/JM→A⊗A0N/JN→0．又A0是半单的，故有正合列0→K/JK→M/JM→N/JN→0．再根据引理1，有JK=K∩JM．引理2证毕．

定理1的证明 由题设JK=K∩JM，再根据引理2，可得正合交换图1，显然有如图3所示的行列正合的交换图．

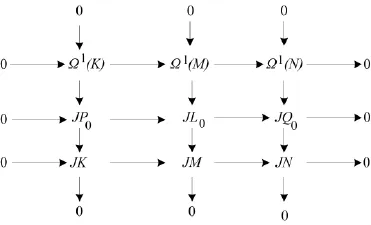
图3 正合交换图之三

将加法函子A/Jk⊗A作用于正合交换图3，再根据引理1，可得如图4所示的行列正合的交换图．

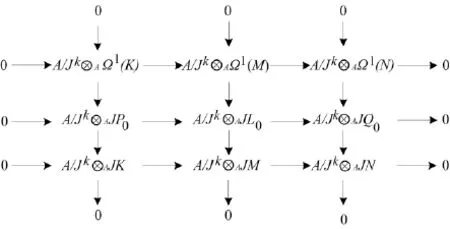
图4 正合交换图之四

根据引理1，有JkΩ1(K)=Ω1(K)∩Jk+1P0．类似地，有如图5所示的行列正合的交换图．

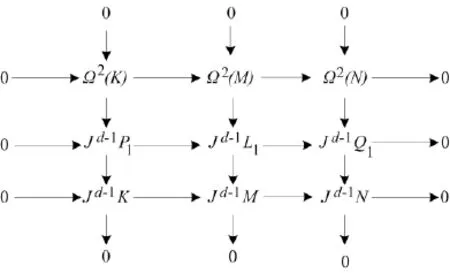
图5 正合交换图之五

将加法函子A/Jk⊗A作用于正合交换图4，再根据引理1，可得如图6所示的行列正合的交换图．

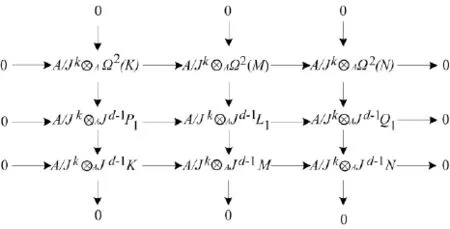
图6 正合交换图之六

再根据引理1，有 JkΩ2(K)=Ω2(K)∩Jk+d-1P1．

对于i≥3的情形，重复上述步骤，均可类似得证．定理1证毕．

［1］Priddy S．Koszul resolutions［J］．Trans Amer Math Soc，1970，152(1):39-60．

［2］Berger R．Koszulity for nonquadratic algebras［J］．J Alg，2001，239(3):705-734．

［3］Green E L，Marcos E，Marínez-Villa R，et al．d-Koszul algebras［J］．J Pure Appl Alg，2004，193(1):141-162．

［4］Martínez-Villa R，Zacharia D．Approximations with modules having linear resolutions［J］．J Alg，2003，266(2):671-697．

［5］吕家凤，何济位，卢涤明．具有 d-Koszul子模滤的分次模［J］．数学年刊，2007，28(2):231-238．