超立方体网络的容错哈密顿Laceability＊

叶彩月， 马美杰， 王维凡

(浙江师范大学数理与信息工程学院，浙江金华 321004)

人们通常用连通的简单图G=(V，E)表示互连网络拓扑结构，其中V和E分别表示图G的点集和边集．本文未定义的记号和术语见文献［1］．

以 u，v为端点的边记为(u，v);以 u，v为端点的路用 P(u，v)或 P(u，v)=〈u，P(u，s)，s，t，P(t，v)，v〉表示，其中P(u，s)和P(t，v)分别表示P(u，v)中u到s的子路和t到v的子路;用E(P)表示路P的边集;2个端点相同的路称为圈，记为C．包含图中所有点的路称为哈密顿路;包含图中所有点的圈称为哈密顿圈．如果图中有一条哈密顿圈，则称它是哈密顿的;如果图中任何2个不同点之间都有哈密顿路，则称它是哈密顿连通的．若图的顶点集可以划分为2个非空子集Vw和Vb，使得对图的任意一条边(u，v)∈E，有 u∈Vw，v∈Vb，则称该图为二部图，记为 G=(Vw∪Vb，E)．在二部图中，如果位于不同部分的任意2个顶点u∈Vw，v∈Vb之间都有哈密顿路，则称二部图是哈密顿Laceable．

大型互连网络的结点和连线在使用过程中难免会发生故障，因此考虑发生故障的网络具有现实意义．如果对图G的任意故障点(或边)集F⊂V(G)(或E(G))且|F|≤k，图G-F仍是哈密顿的，则称图G是k点(或边)容错哈密顿的．对二部图G的任意故障集F⊂V(G)∪E(G)且|F|≤k，图G-F仍是哈密顿Laceable，则称图G是k容错哈密顿Laceable．

n维超立方体网络Qn(或简称为n立方体)由2n个顶点构成，每个顶点v用一个n位二进制串v0v1…vn-1表示．2个顶点相连当且仅当2个顶点对应的二进制串恰有一位分量不同．特别地，Qn是点可迁和边可迁的二部图(Vw∪Vb，E)［1］．

由Qn的定义知，Qn可分解为2个Qn-1添加一些边集构成:Qn=Lk⊙Rk．其中:Lk表示Qn中第k个分量为0的点导出的子图;Rk表示Qn中第k个分量为1的点导出的子图．Qn中连接Lk和Rk的2n-1条边称为Qn的k维边，记为Ek．称Qn=Lk⊙Rk为Qn的一个k维划分．

引理1［2］当n≥3时，超立方体网络Qn的fe条故障边集设为Fe．若fe≤2n-5，且Qn-Fe中每个顶点至少与2条非故障边相关联，则Qn-Fe是哈密顿Laceable．

引理2［3］当n≥3时，超立方体网络Qn的故障集为F=Fav∪Fe．其中:Fe表示fe条故障边集;Fav表示fav对不相交的相邻故障点对集．则

1)当0≤fav≤n-2，fe+fav≤n-2 时，Qn-F 是哈密顿的;

2)当0≤fav≤n-3，fe+fav≤n-2 时，Qn-F 是哈密顿 Laceable．

引理3［3］当n≥3时，超立方体网络 Qn=(Vb∪Vw，E)的 fe条故障边集设为 Fe．若 fe≤n-3，则在Qn-Fe中任意点 w'，w"∈Vw，b'，b"∈Vb间有 2 条内不交的路 P(w'，b')和 P(w"，b")，分别连接 w'，b'和 w"，b"，且 V(P(w'，b'))∪V(P(w"，b"))=V(Qn)．

引理4［3］当n≥4时，超立方体网络Qn=(Vb∪Vw，E)的 fe条故障边集设为Fe．若fe≤n-4，则任意点 w，w'∈Vw，b，b'∈Vb在 Qn-Fe-{w'，b'}中存在一条哈密顿路 P(w，b)．

引理5［4］当n≥3时，超立方体网络Qn=(Vb∪Vw，E)的 fe条故障边集设为Fe．若fe≤n-3，则任意点 w'，w"∈Vw，b'∈Vb在 Qn-Fe-{b'}中存在一条哈密顿路 P(w'，w")．

定理1 当n≥3时，超立方体网络Qn的故障集为F=Fav∪Fe．其中:Fe表示fe条故障边集;Fav表示fav对不相交的相邻故障点对集．若0≤fav≤n-3，fe+2fav≤2n-5，且Qn-F中每个顶点至少与2条非故障边相关联，则Qn-F是哈密顿Laceable．

证明 对超立方体的维数n(n≥3)用数学归纳法证明．当n=3时，fav=0，fe≤1，由引理1知，定理1成立．

当n=4时，fav=0，fe≤3或 fav=1，fe≤1，由引理1和引理2知，定理1成立．

设定理1在Qn-1中成立．下证定理1在Qn(n≥5)中也成立．

由引理1知，当 fav=0 时，定理1成立．下设1≤fav≤n-3．因为 fe+2fav≤2n-5，所以 fe≤2n-7．在Qn-F中至多有1个点与n-2条故障边相关联．否则，如果存在2个点与n-2条故障边相关联，那么fe≥2n-5，这与 fe≤2n-7 矛盾．用 Eav={(wi，bi)|{wi，bi}⊂Fav}表示故障点对之间的边集．因此

1)若存在一个点v与n-2条故障边集Ev相关联，则由于故障点对集fav≤n-3，因此存在Qn的一个 k 维划分，使得 Ev∩Ek=1，Ek∩Eav= φ;

2)若每个点都至多与n-3条故障边相连，则存在Qn的一个k维划分，使得Ek∩Eav=φ．

所以，存在Qn的一个划分Qn=L⊙R，使得L和R中任意一点都至少与2条非故障边相关联，且故障点对{wi，bi}∈V(L)或者{wi，bi}∈V(R)．将连接 L 和 R 的边集记为 Ec．令

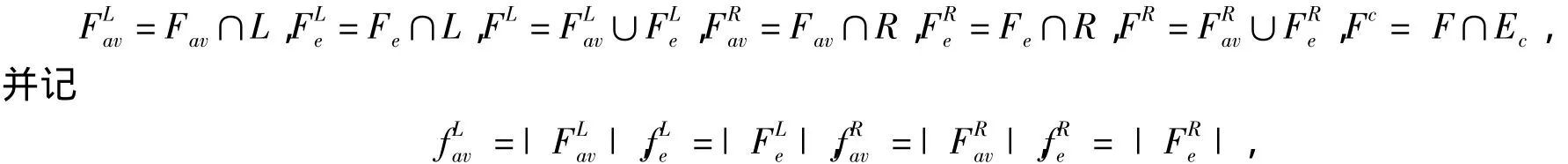
则

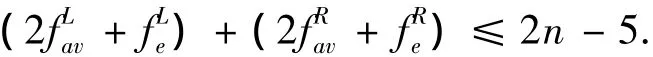
不妨设

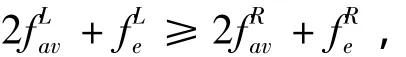
则

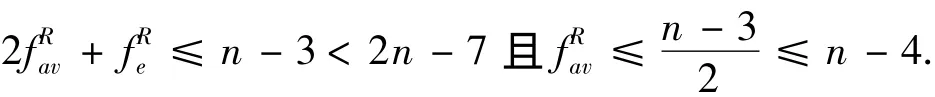
因此R满足归纳假设，即R-FR是哈密顿Laceable．

下证对Qn-F中的任意位于不同部分的2个点w∈Vw，b∈Vb存在一条哈密顿路连接w和b．分以下2种情形讨论:

情形 1．1 w，b∈V(L-FL)或 w，b∈V(R-FR)，不妨设 w，b∈V(L-FL)．

由归纳假设知，在L-FL中存在一条哈密顿路P(w，b)．由于

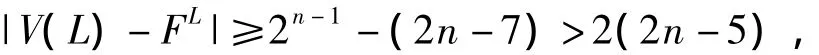
因此，在路 P(w，b)上存在一条边(x，y)，使得边(x，xR)，(y，yR)为非故障边，且点 xR，yR为非故障点(其中 xR与 yR分别表示 x与 y在 R 中的邻点)．记 P(w，b)=〈w，P(w，x)，x，y，P(y，b)，b〉．根据归纳假设，在R-FR中有一条哈密顿路P(xR，yR)，因此在Qn-F中有一条哈密顿路

情形 1．2w∈V(L-FL)，b∈V(R-FR)或者 w∈V(R-FR)，b∈V(L-FL)．不妨设 w∈V(L-FL)，b∈V(R-FR)．

在L-FL中存在点z∈Vb，使得(z，zR)为非故障边，且zR为非故障点(其中zR表示点z在R中的邻点)．根据归纳假设，在L-FL和R-FR中分别有一条哈密顿路P(w，z)和P(zR，b)，因此在Qn-F中有一条哈密顿路 P(w，b)=〈w，P(w，z)，z，zR，P(zR，b)，b〉．

断言1 在L-FL中存在一对相邻故障点对{w1，b1}，使得L-(FL-{w1，b1})中位于不同部分的任意两点w'∈Vw，b'∈Vb在L-(FL-{w1，b1})中存在一条哈密顿路P连接w'和b'，满足w1与b1在路P上的邻点不与L之外的故障边关联．

证明 如果Fc=φ，则由归纳假设知，L-(FL-{w1，b1})中有一条哈密顿路P连接w'和b'，显然w1与b1在路P上的邻点不与L之外的故障边关联．

如果 Fc={(u，v)}者存在故障点wi与u之间的邻边是故障边，并设此故障点为w1，则由归纳假设知，L-(FL-{w1，b1})中有一条哈密顿路P连接w'和b'，显然w1在P上的邻点不能为u．如果任意故障点wi都与u相邻且邻边都是非故障边，则由故障点对fav≥1知，在L中存在故障点(设为w1)与u相邻，且边(u，w1)是非故障边．由归纳假设知，L-(FL-{w1，b1})-(u，w1)中有一条哈密顿路P连接w'和b'，使得u与w1在P上不相邻．

因此，断言1成立．

根据断言1，分下列3种子情形来构造Qn-F中连接w与b的哈密顿路:

情形2．1 w，b∈V(L-FL)．由断言1 知，存在一对相邻故障点对{w1，b1}，使得L-(FL-{w1，b1})中存在一条哈密顿路P(w，b)，满足w1与b1在路P上的邻点不与L之外的故障边关联．

如果(w1，b1)∉E(P(w，b))，并设 P(w，b)=〈w，P(w，s)，s，w1，t，P(t，x)，x，b1，y，P(y，b)，b〉，且(s，sR)，(t，tR)，(x，xR)，(y，yR)都是非故障边，则由引理3 知，在 R-FR中存在 2 条内不交路 P(sR，xR)和P(tR，yR)包含R-FR中的所有点．因此，在Qn-F中存在一条哈密顿路(如图1(a)所示)

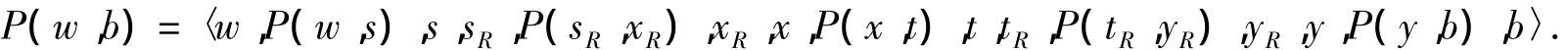
如果(w1，b1)∈E(P(w，b))，并设 P(w，b)=〈w，P(w，x)，x，w1，b1，y，P(y，b)，b〉，则由引理 1 知，R-FR中有哈密顿路P(xR，yR)，因此在Qn-F中存在一条哈密顿路

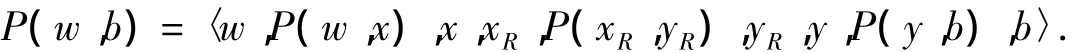
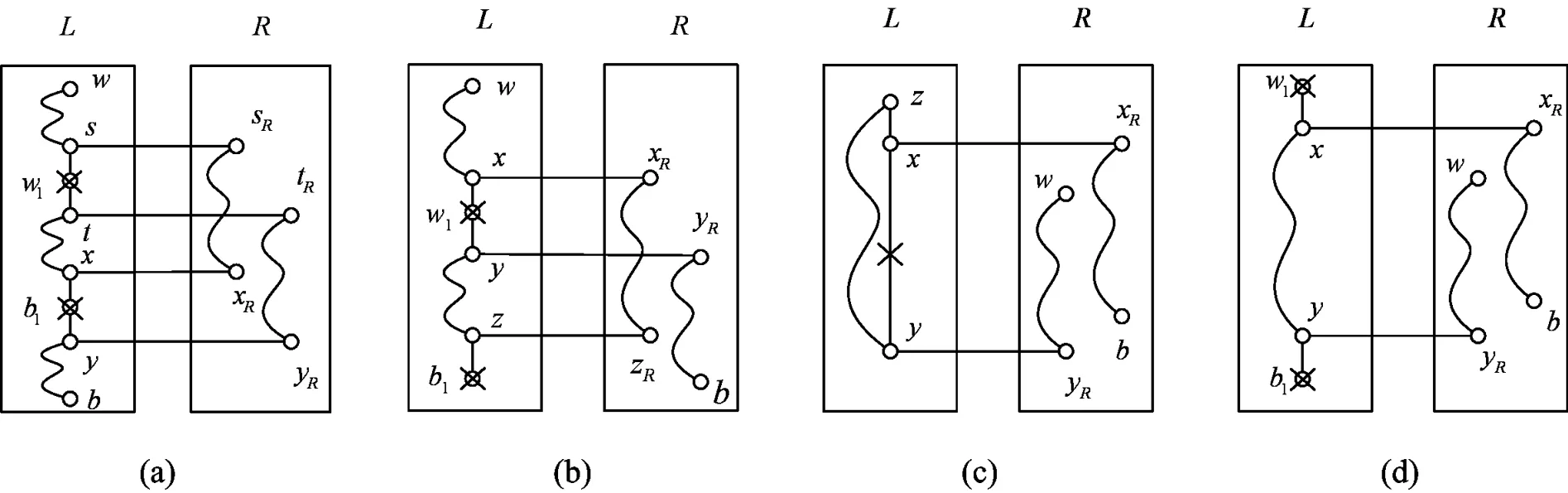
图1 Qn-F中的哈密顿路

情形2．2 w∈V(L-FL)，b∈V(R-FR)．由断言 1 知，存在一对相邻故障点对{w1，b1}，使得L-(FL-{w1，b1})中存在一条哈密顿路P(w，b1)，满足w1与b1在路P上的邻点不与L之外的故障边关联．

如果(w1，b1)∉E(P(w，b1))，则可设 P(w，b1)=〈w，P(w，x)，x，w1，y，P(y，z)，z，b1〉．如果 zR≠b，则由引理3知，在R-FR中存在2条内不交路P(xR，zR)和P(yR，b)包含R-FR中的所有点．因此，在Qn-F中存在一条哈密顿路(如图1(b)所示)

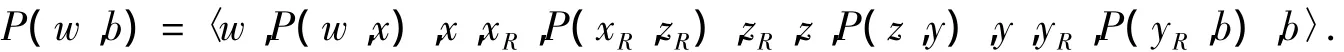
如果zR=b，则由引理5知，R-FR-{b}中有哈密顿路P(xR，yR)．因此，Qn-F中存在一条哈密顿路

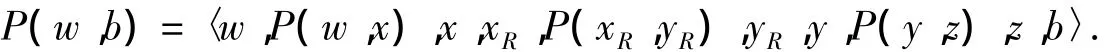
如果(w1，b1)∈E(P(w，b1))，并设 P(w，b1)=〈w，P(w，x)，x，w1，b1〉，则由引理 1 知，R-FR中有哈密顿路P(xR，b)．因此，Qn-F中存在一条哈密顿路

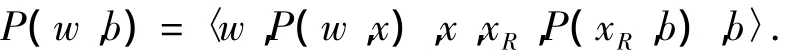
情形 2．3 w，b∈V(R-FR)．当 n=5，fRe=1时，分以下2种情形讨论:

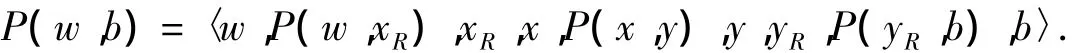
如果 xR≠b，yR=w 或者 xR=b，yR≠w，不妨设 xR≠b，yR=w，则由引理5 知，R-FR-{b}中存在哈密顿路P(w，yR)．因此，Qn-F中有一条哈密顿路

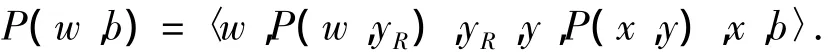
当(x，y)∉E(C)时，与①类似，在Qn-F中存在一条哈密顿路P(w，b)．

综上所述，定理1得证．

注1 如果故障点对fav=n-2，则定理1不成立．如在Q3中，当点000，010为故障点对时，Q3中点101到点111无哈密顿路(如图2(a)所示)．故定理1中的界0≤fav≤n-3是紧的．

注2 如果故障数fe+2fav=2n-4，则定理1不成立．如在Q4中，当点0000，0010为故障点对，(0110，1110)，(0011，1011)为2条故障边时，Q4中任意一点都至少关联于2条非故障边，此时fe+2fav=2+2=8-4=4，而点0101到点0111无哈密顿路(如图2(b)所示)．故定理1中的界fe+2fav≤2n-5是紧的．

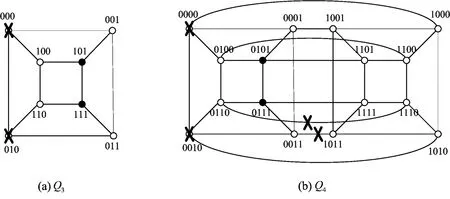
图2 Q3，Q4中无哈密顿路的情形

［1］徐俊明．组合网络理论［M］．北京:科学出版社，2007．

［2］Tsai C H．Linear array and ring embeddings in conditional faulty hypercubes［J］．Theoretical Computer Science，2004，314(3):431-443．

［3］Hung Chunnan，Chang Yihua，Sun Chaoming．Longest paths and cycles in faulty hypercubes［C］//Proceedings of the 24th IASTED International Conference on Parallel and Distributed Computing and Networks．Innsbruck:ACTA Press Anaheim，2006:101-110．

［4］Tsai C H，Jimmy J M T，Hsu L H．Fault-tolerant hamiltonian laceability of hypercubes［J］．Information Processing Letters，2002，83(6):301-306．