一阶中立型差分方程的振动性

陈春华

(周口师范学院化学系,河南周口466000)

近几年来,关于差分方程解的振动性质的研究引起了大批学者的兴趣[1-6]。本文考虑一阶中立型差分方程

其中Δ为向前差分算子,即Δxn=xn+1-xn;p,q, τ,σ为正常数,且 p∈(0,1)。

文献[1]给出了在01和τ-σ=1两种情况下对方程(1)的振动性进行研究。

定义1 方程(1)的解{xn}称为振动的,如果xn既不最终为正,也不最终为负;否则,称为非振动的。

1 主要结果

引理1[6]方程(1)的所有解振动的充分必要条件是其特征方程

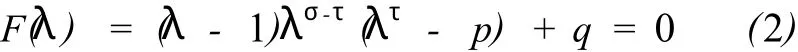
没有正实根。

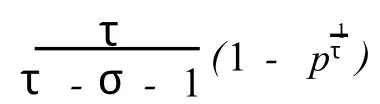
证 由于 F(λ)=(λ-1)λσ-τ(λτ-p)+q= 0且q>0,所以只有(λ-1)λσ-τ(λτ-p)<0时方程才可能有根,而00,方程没有实根,所以特征方程只有在区间(p,1)内可能有正实根。

因为 F(λ)=(λ-1)λσ-τ(λτ-p)+q在[p,1]上连续,所以 F(λ)在[p,1]有最大值和最小值。显然在边界点上 F(1)=F(pτ1)=q取得最大值,那么在(p,1)内至少存在一点ξ,使得 F(ξ)为最小值。显然函数 F(λ)=(λ-1)(λτ-p)+q在区间(p,1)内是连续可导的,故ξ点也为极小值点。由费马定理知,F′(ξ)=0,即

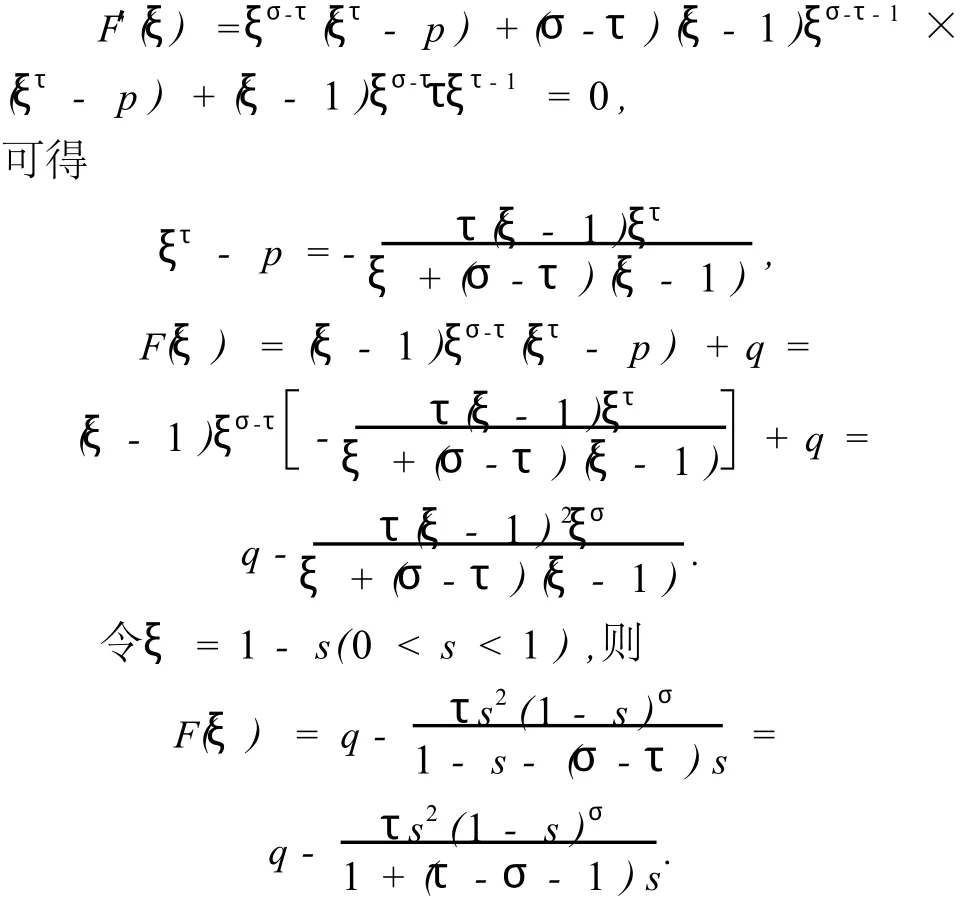
由τ-σ>1得τ-σ-1>0,所以(τ-σ+1)s> 0,因此

[1]陈晓童,王保平.一种新型的图像去噪滤波器[J].河北理工学院学报,2003,25(3):52-55.

[2]关新平,赵立兴,唐英干.图像去噪混合滤波方法[J].中国图像图形学报,2005,10(3):332-337.

[3]金良海,李德华.基于噪声检测的图像去噪算法[J].模式识别与人工智能,2008,21(3):28-32.

[4]Rafael C Gonzalez,Richard EWoods,Steven L Eddins.数字图像处理(MA TLAB版)[M].北京:电子工业出版社,2005:117-120.

[5]李威,郁道银,谢洪波,等.基于领域信息优化方法的图像恢复与增强[J].天津大学学报,2001,34(4): 495-498.