基于Matlab的单螺杆泵线型打扣分析
韩道权,韩 超,丁宝林,叶卫东
(1.东北石油大学机械科学与工程学院,黑龙江大庆163318;2.大庆油田装备制造集团,黑龙江大庆163255) ①
基于Matlab的单螺杆泵线型打扣分析
韩道权1,韩 超1,丁宝林2,叶卫东1
(1.东北石油大学机械科学与工程学院,黑龙江大庆163318;2.大庆油田装备制造集团,黑龙江大庆163255)①
根据单螺杆泵定子骨线及其等距曲线的形成原理,利用Matlab软件对单螺杆泵定子骨线打扣现象进行了深入剖析,并利用数值法绘出了单螺杆泵定子头数、变幅系数和不打扣条件下的最大等距半径之间的关系图形。结果表明:当定子头数确定时,变幅系数与不打扣最大等距半径的关系曲线为递减规律;当变幅系数确定时,定子头数越小,允许的不打扣半径越大。
螺杆泵;曲线;干涉;数学分析
1 单螺杆泵定子骨线方程
定子骨线的研究主要是在复平柱面坐标系下,它与常规的空间直角坐标系O-x-y-z的不同之处在于以复平面1-O-j取代实平面x-O-y,并取向下方向为z轴正方向。复平柱面坐标系中,O-1称为实轴,单位是1;O-j称为虚轴,单位是,如图1所示。单螺杆泵定子骨线是将半径为r的滚圆沿半径为R的导圆做相对纯滚动时,滚圆平面上任意点A在导圆平面上形成的轨迹。3头定子骨线如图2所示,圆O1为导圆,圆O2为滚圆。定子骨线在复平柱面坐标系下的方程[1-2]为
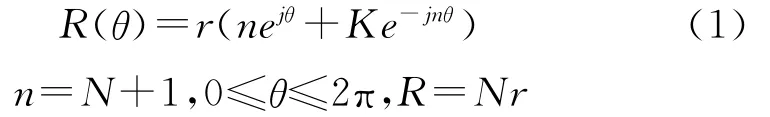
式中,n为转子的头数;K为变幅系数,即发生点A到滚圆圆心O2的距离与r的比值。

图1 复平柱面坐标系
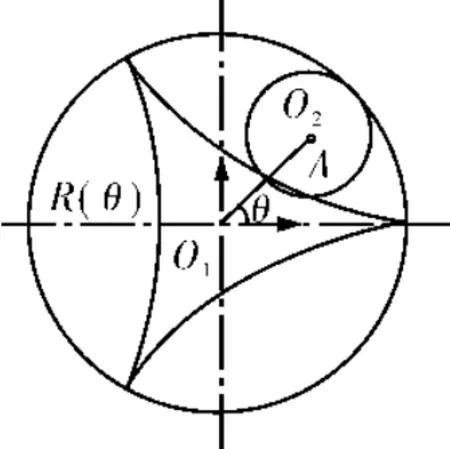
图2 3头定子骨线
2 定子轮廓线打扣现象分析
单螺杆泵定子轮廓线是圆心在骨线上、半径为ra的一系列圆外包络(即等距曲线)得到的。因此,当等距圆上外包络点出现回行时,就会产生打扣现象[3-4],如图3所示。
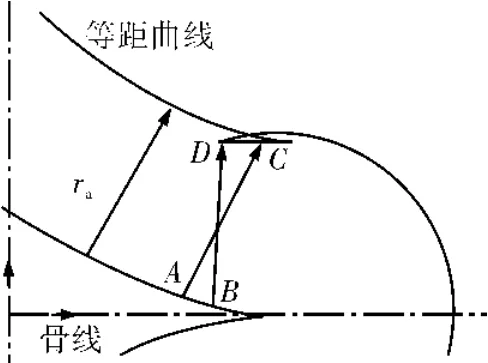
图3 等距曲线打扣
点A在等距曲线上的等距点为C,点B的等距点为D,D点出现了回行,这时就产生了打扣现象,即打扣现象产生的根本原因就是骨线上任意2点相邻的法线在等距半径范围内有交点。这时生产出来的定子并不是严格的摆线等距曲线。如果打扣较小,唯一的解决办法是通过橡胶的过盈来进行补偿,但是如果打扣较大,则不能用这种方法解决。
由式(1)可得到骨线在复平柱面坐标系下的切线方程为[5-8]
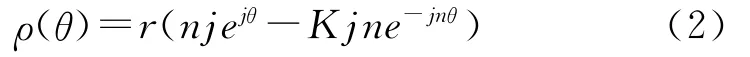
由式(2)可得直角坐标系下坐标方程为
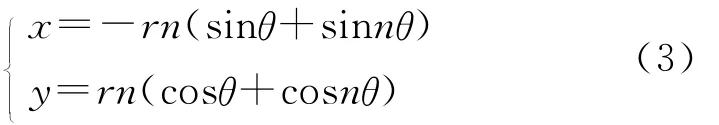
由式(3)可推出,骨线在直角坐标系下任意点的切线方程为

由式(3)~(4)可得骨线任意点上的法线方程为
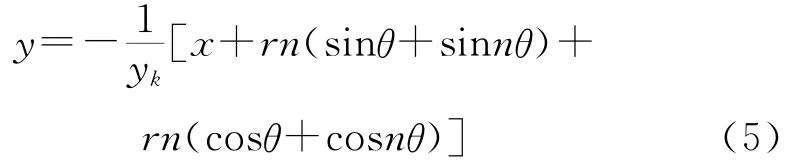
通过上述公式利用软件绘制定子骨线及其法线图形。由于定子骨线是轴对称图形,因此,只研究其1个对称区间的图形即可。当K=1时,定子骨线及其法线图形如图4所示。当θ=0时,法线是垂直的,它与其他法线的焦点随着θ的减小而越来越接近骨线,这时无论等距半径取多大,等距曲线都会产生打扣现象。这也是由于骨线在θ=0处为尖点所致。

图4 K=1时3头骨线及其法线
K=0.8时,骨线及其法线图形如图5所示。可以看出,在θ=0处,骨线为弧形,因此法线是水平的,而后法线斜率先递增,后递减。但法线在一定范围内彼此间仍有交点。因此,等距曲线的打扣现象是在等距半径增大到一定范围内产生的。

图5 K=0.8时3头骨线及其法线
K=0.5时,骨线及其法线图形如图6所示。可以看出,在θ=0处法线仍是水平的,而后法线呈递增规律。法线在骨线外侧是发散的,没有交点,这时无论等距半径取多大,等距曲线都不会产生打扣现象。
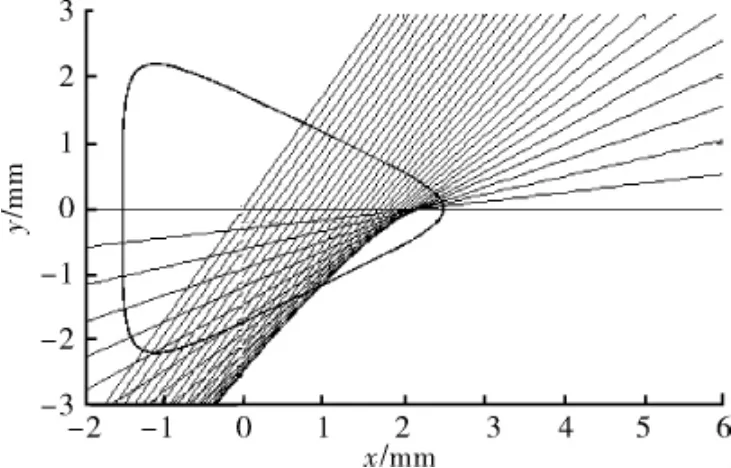
图6 K=0.5时3头骨线及其法线
以3头单螺杆泵骨线为例,通过Matlab绘制定子骨线法线斜率图形,进一步直观判断定子打扣现象。图7自下而上分别是K为0.1~0.9(步长0.1)时法线斜率;K=1时法线斜率如图8所示。
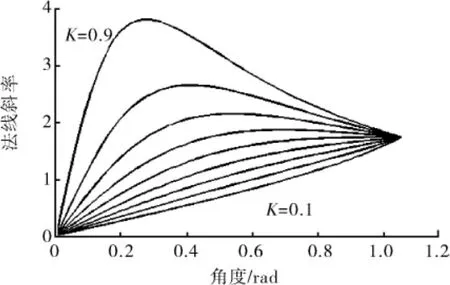
图7 K=0.1~0.9时3头骨线法线斜率
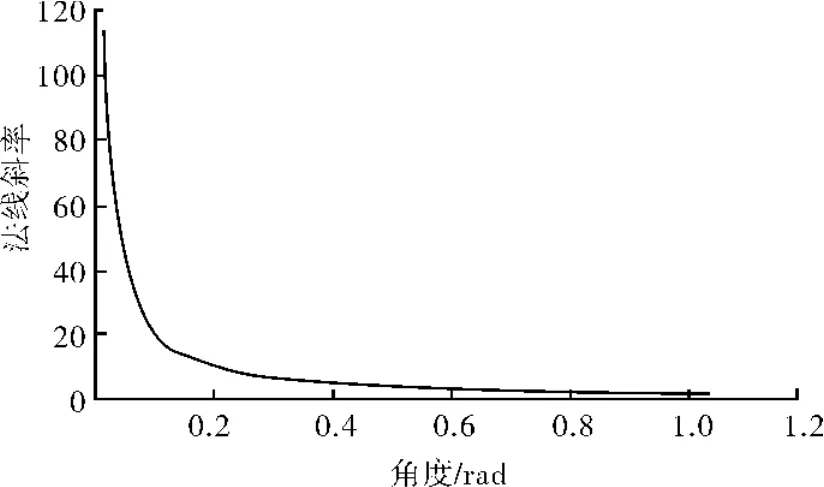
图8 K=1时3头骨线法线斜率
如图7所示,当K趋近于0时,斜率曲线向右下方下凹,并且单调递增。随着K的增加,曲线下凹趋势不断变缓,直至上凸。如图8所示,当K=1时,上凸曲线左侧消失,只剩下右侧,变成唯一一条向左下方下凹的曲线,此时,在θ=0处法线是垂直的。当K<1时,骨线在θ=0处为弧形,因此法线为水平方向。当法线斜率单调递增时,彼此之间就不会有交点;当法线斜率先递增后递减时,打扣现象是在一定范围内产生的;当法线递减(K=1)时,定子轮廓线永远打扣。
3 数值法求解不打扣最大等距半径
通过上述分析可知,定子轮廓线不打扣的最大等距半径即为骨线外侧法线交点到骨线距离中的最小值。基于这个条件,用Matlab进行编程,求出这个最小值,过程如下:

通过上述程序可以找到在n、K条件下定子不打扣的最大等距半径,并得到1组头数不变、K变化的数据。通过曲线拟合的形式可以做出不同头数、变幅系数与最大等距半径之间的关系图形,如图9所示。图9中,取ra=1,即单位摆线;当ra的值不为1时,最大等距半径数值上等于单位摆线的等距半径乘以滚圆半径。
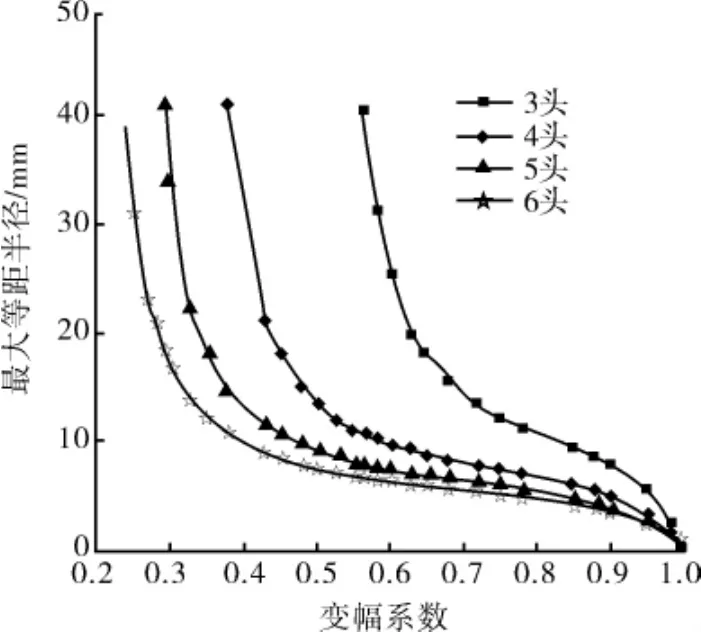
图9 3~6头骨线最大等距半径曲线
由图9可以看出,定子不打扣的最大等距半径是随着变幅系数的增加而逐渐减小的;图中清晰地反应出了定子头数、最大不打扣等距半径和变幅系数K三者之间的关系。例如,当K=0.85时,从图中可得3~6头定子不打扣的最大等距半径分别为9.4、5.9、4.7和4.2mm,即头数越少,允许的不打扣等距半径越大。
普通内摆线是当式(1)中K=1时的摆线,共轭曲线副是定转子头数相差1得到的。短副内摆线型单螺杆泵是短副内摆线做定子骨线,用被定子骨线内包络的共轭曲线作为转子骨线。因此,如果定子是不打扣的,那么用这种包络曲线的方法得到的转子骨线及其等距曲线也是不打扣的[5]。因此,只要保证基础骨线R(θ)的等距曲线不打扣,就可以得到严格的定转子共轭曲线。基础骨线的等距曲线打扣条件遵从图9的规律。
4 结论
1) 当变幅系数K=1时,等距曲线永远打扣;当0<K<1时,等距曲线永远不打扣。
2) 当变幅系数K趋近于1时,不打扣等距半径迅速下降,越接近1,可用等距半径越小。
3) 不同头数、相同变幅系数、头数越少时,允许的不打扣等距半径越大。
4) 相同头数、变幅系数越小时,允许的不打扣等距半径越大。
[1] 苏义脑,谢竹庄.螺杆钻具马达线型分析基础及研究方法[J].石油机械,1985,13(6):10-20.
[2] 杜秀华,任 彬,韩国有.双头单螺杆泵的线型设计及虚拟建模[J].石油矿场机械,2007,36(1):33-35.
[3] 万邦烈.单螺杆泵式水利机械的研究与开发[J].石油矿场机械,1995,24(3):14-18.
[4] 熊建新,陈次昌,魏存祥.双头单螺杆泵衬套线型分析[J].石油机械,2008,36(12):31-33.
[5] 宋玉杰,温后珍,孟碧霞.单螺杆式水力机械变幅系数的选择[J].中国机械工程,2010,21(18):69-71.
[6] 王国庆,师国臣,马志权,等.大庆油田螺杆泵机采井系统效率现状及对策[J].石油矿场机械,2011,40(7):25-28.
[7] 韩国有,姜长鑫,杜秀华.普通内摆线型双头螺杆泵建模及运动仿真[J].石油矿场机械,2011,40(1):1-4.
[8] 王春阳,夏秀文,李良军,等.预轮廓定子螺杆钻具性能研究[J].石油矿场机械,2011,40(5):90-92.
Analysis of Linear Dozen Buckle of Single Screw Pump Based on Matlab
HAN Dao-quan1,HAN Chao1,DING Bao-lin2,YE Wei-dong1
(1.College of Mechanical Science and Engineering,Northeast Petroleum University,Daqing163318,China;2.Daqing Petroleum Equipment Group,Daqing163255,China)
According to formation mechanism of stator skeleton lines and its isometric profiles of screw pump,the phenomenon of Dozen buckle of bone line of single screw pump stator has been analyzed by mathematical software Matlab,the relationship between the different number of single screw pump stator,the radius variation ratio and the radius of the maximum isometric under the condition of no dozen buckle has been painted out.The results show that:when the stator head is determined,the radius variation ratio and the radius of the maximum isometric show a decreasing trend;when the radius variation ratio is determined,the fewer the number of stator head,the larger the radius.
screw pump;curve;interaction;mathematic analysis
1001-3482(2011)12-0038-04
TE933.3
A
2011-06-13
黑龙江省教育厅科技攻关项目(11551014)
韩道权(1966-),男,黑龙江大庆人,副教授,主要从事机械设计制造及其自动化研究,E-mail:handq2003@163.com。

