二氧化碳/甲烷/氮气二元混合物在有序介孔碳材料CMK-3中的吸附和分离
彭 璇 张勤学 成 璇 曹达鹏
(1北京化工大学信息科学与技术学院,北京100029;2北京化工大学理学院,北京100029; 3北京化工大学有机无机复合材料国家重点实验室材料分子设计模拟研究室,北京100029)
二氧化碳/甲烷/氮气二元混合物在有序介孔碳材料CMK-3中的吸附和分离
彭 璇1,*张勤学2,3成 璇3曹达鹏3
(1北京化工大学信息科学与技术学院,北京100029;2北京化工大学理学院,北京100029;3北京化工大学有机无机复合材料国家重点实验室材料分子设计模拟研究室,北京100029)
采用分子模拟与吸附理论研究了天然气成分在有序介孔碳材料CMK-3上的吸附和分离.巨正则系综蒙特卡罗(GCMC)模拟表明,CH4和CO2气体的较优存储条件分别为208 K、4 MPa和298 K、6 MPa,其最大超额吸附量分别为10.07和14.85 mmol·g-1.基于双位Langmuir-Freundlich(DSLF)模型,使用理想吸附溶液理论(IAST)预测了不同二元混合物在CMK-3中的分离行为,发现吸附选择性SCO2/CH4与SCH4/N2比较接近,在298 K和4 MPa下约等于3,而N2-CO2体系中的CO2吸附选择性较高,可达到7.5,说明CMK-3是一种适合吸附和分离天然气组分的碳材料.
巨正则系综蒙特卡罗;吸附选择性;理想吸附溶液理论;甲烷;二氧化碳;氮气;CMK-3
1 引言
煤石油天然气资源的枯竭和温室效应的加剧,迫使各国研究人员加速研发高效存储甲烷氢气能源和捕捉二氧化碳气体的技术.相比于液化和压缩技术,吸附技术在操作安全性、低成本和能源效率方面具有一定的优势,因此制备新型多孔材料并应用于气体吸附和分离一直是国际性的学术前沿和研究热点.Jun和Ryoo1基于模板碳化技术,2以蔗糖为碳源和介孔硅材料SBA-15为模板,成功地制备出了一种结构呈六方形排列的新型介孔碳材料CMK-3.该材料的水热稳定性较好、比表面积较高、孔道结构规则有序、孔径分布狭窄和孔径大小连续可调,有望在吸附、分离、催化和光电磁等领域得到广泛的应用.3
目前研究者们已对CMK-3材料上的吸附开展了一些实验和模拟工作,4-7如Zhou等5制备了CMK-3材料并使用体积法测量了N2、CH4和CO2等小分子气体的吸附等温线;Xia等6在CO2活化的CMK-3材料上研究了H2的吸附存储,发现活化后储氢量有明显改善,在77 K和105Pa下能达到2.27% (w);Monk等7采用分子动力学方法模拟了CMK-3材料孔中[dmim+][Cl-]型离子液体的结构和动力学性质.值得一提的是,Zhou等5根据实验测量的纯气体吸附等温线推测CMK-3可能是一种适合分离混合物中CO2的材料,但此观点有待实验和理论上的支持.更重要的是,CMK-3材料上的微观吸附机理还不是很清楚.为此,本文将采用计算手段去研究该材料上的气体吸附及分离性质.
研究吸附现象的计算方法主要有分子模拟8和吸附理论9两种.许多研究者提出了不同的吸附理论模型,如理想吸附溶液理论(IAST),10二维状态方程,9,11简化局部密度函数理论,12Ono-Kondo模型.13近年来基于双位Langmuir-Freundlich模型(DSLF)的IAST在碳材料的吸附分离研究中得到广泛应用,14,15我们将采用该方法来预测常温下CMK-3中的分离效果,为吸附工艺条件的设计与优化提供理论上的依据.
本文的工作由以下部分组成:(1)对CMK-3材料结构进行了模型化,建立了有效表征流体与碳层间的相互作用的势能模型;(2)利用巨正则蒙特卡罗(GCMC)方法8,16模拟优化了CH4和CO2纯气体在CMK-3上的存储条件;(3)利用IAST评价了CH4-N2、CO2-CH4及CO2-N2二元体系的吸附分离性能.

图1 CMK-3材料模型示意图Fig.1 Schematic diagram of CMK-3 material
2 CMK-3材料结构的模型化
Ryoo等4通过透射电子显微镜(TEM)和X射线衍射(XRD)实验,以及密度泛函理论(DFT)分析,建立了CMK-3的结构模型,其示意图如图1所示.本文将借鉴Ryoo等提出的结构模型16进行分子模拟研究.由图1可知,一个基本的模拟晶胞由四根呈六方排列的碳柱构成,其中a为单元晶胞的结构参数,d为模拟碳柱的直径,孔间距(H)定义为H=(2a/ 31/2)-d.尽管CMK-3材料在结构上长程有序,但从原子水平上观察,则近程无序.对于这种本质上为无定形碳的材料,常规的理论方法难以描述原子水平的微观结构.为对该结构模型进一步简化,我们假设碳柱由一组同轴心的、层间距为0.34 nm的单原子层构成.这种处理方式在其他类CMK材料的吸附模拟17-19中取得了较好的效果.
3 分子模拟
3.1 理想化势能模型
任一流体分子在CMK-3材料孔中的总势能ΦT可表示为两部分之和,一部分是流体分子与其它流体分子之间的势能Φff,另一部分是流体分子与碳层之间的势能Φsf,即

由于模拟中连续势能总是要被截断,因此计算流体分子之间的势能时采用截断漂移势能8

式中ΦLJ为12-6 Lennard-Jones(L-J)势能,rc为截断半径,rc=5σff,σff是流体分子LJ势的尺寸参数.流体分子与单个碳层之间的作用势由Gordon模型20计算:

表1 Lennard-Jones势能模型参数Table 1 Parameters of Lennard-Jones potential models
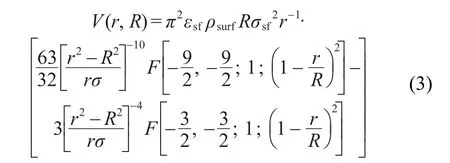
其中F[α,β;γ;χ]为超比几何函数,R表示单个碳层的半径,r表示流体分子到碳层的距离,ρsurf为二维碳层密度,ρsurf=38.2 nm-2,εsf与σsf分别表示流体分子与碳原子之间的能量与尺寸相互作用参数,由Lorentz-Berthelot混合规则计算.不同流体分子与碳原子的L-J势能模型参数在表117,21,22中列出.
3.2 有效势能模型
由于上文描述的是一个高度理想化的模型,该模型对流体与碳层间的相互作用的表征并不十分准确,因此为了有效地描述流体与碳层间的相互作用,我们在高度理想化模型的基础上,对计算流体与碳层交互作用的Lorentz-Berthelot混合规则引入可调参数ksf21

通过吻合吸附等温线的实验与模拟结果来确定一个有效的交互作用参数ksf,从而使得该模型能有效地表征流体分子与碳层间的相互作用.
3.3 模拟细节
采用化学势µ、体积V和温度T固定的GCMC方法研究流体分子在CMK-3材料中的吸附.模拟中,碳柱长度取20 nm,同时在x、y、z三维方向上施加周期边界条件.每个模拟条件产生2×107个构型,其中最初的1×107个构型将被丢掉,以确保模拟平衡和消除初始构型的影响.而在计算热力学量的系综平均时,只对后面1×107个构型进行统计,其总势能和平均数密度的统计偏差都在2%以内.通常实验中测量的吸附量为超额性质,即排除吸附相体积被主体相气体所填充后的吸附量,而分子模拟计算则为绝对性质.为将分子模拟结果与实验结果比较,根据以下关系式将绝对吸附量Na转换成超额吸附量Nex

其中ρb为气体主体密度,由Peng-Robinson状态方程计算得到,V为吸附剂的自由体积.
4 吸附理论
4.1 双位Langmuir-Freundlich模型
纯组分吸附的等温线由DSLF模型14,15关联,回归的模型参数用于IAST进行混合物的吸附预测. DSLF模型由如下等式描述

其中f为主体气体在吸附平衡时的主体气相逸度, Ni、ki和ni为待回归的模型参数,分别表示i吸附位的最大吸附量、亲和常数以及对简单Langmuir方程的偏离程度.
4.2 理想吸附溶液理论
当达到吸附平衡时,气相与吸附相之间的i组分逸度相等,即

p为气相总压,xi、yi分别为i组分在吸附相、气相的摩尔分数,Φi为由Peng-Robinson状态方程计算的i组分气相逸度系数,fi0为i组分的吸附相逸度,π为吸附表面的扩张压力.对于二元混合物,吸附平衡时两组分的扩张压力相等,即

式中Ni0为组分i在逸度fi时的吸附量.采用数值积分和方程求根的方法,由上式可解出组分i在吸附相中的摩尔分数xi.组分i对j的吸附选择性Sij定义为

5 结果与讨论
5.1 纯组分吸附的分子模拟
5.1.1 确定交互作用参数kfw
为与实验吸附等温线比较,模拟中根据文献5的实验值选取CMK-3材料的结构参数,a=9.8 nm和H=3.8 nm.图2给出了常温下N2、CH4和CO2超额吸附等温线的实验与模拟结果.如图2所示,不进行交互作用参数调整时(ksf=1.0),模拟值普遍低于实验值,表明真实无定形材料的结构复杂性难以用一种简化模型去精确地描述.另外也说明模拟中流体分子与碳柱间的相互作用偏小.同样,Nguyen等23发现如果基于常见的碳-碳作用势参数,使用Lorentz-Berthelot混合规则计算的碳与氢气之间作用也存在偏低的现象.因此,我们适当地上调ksf,发现当ksf= 1.25时吸附曲线的实验值和模拟值均吻合一致,得到的ksf参数可用于GCMC预测中.

图2 298 K下超额吸附等温线的实验与模拟比较Fig.2 Comparison of experimental and simulated excess adsorption isotherms at 298 K(a)N2;(b)CH4;(c)CO2
5.1.2 纯气体吸附存储条件的优化
吸附剂的存储量主要取决于吸附过程的工艺条件.为对实验中的吸附条件进行优化设计,我们模拟了不同温度下CH4和CO2在CMK-3材料中的超额吸附等温线.如图3所示,当压力较低时,孔内吸附流体密度大于主体相流体,提高压力可使超额吸附量增加,压力过高时则相反.因此,每条吸附等温线均存在一个最优的压力使得对应的超额吸附量最大.此外,从图3还可看出,低压下温度的升高会引起超额吸附量的降低,但是高压高温下的超额吸附量反而较大.这可根据等式(5)来解释,对于前者,低压下的主体相密度很低,故对超额吸附的影响忽略不计,而温度的升高使流体分子的动能增加,从而削弱了碳材料对流体分子的吸附能力,导致绝对吸附量的减少;对于后者,高温引起的主体相密度降低对超额吸附的影响占主导作用,明显强于高压引起的主体相密度增加和高温引起的绝对吸附量降低这两种因素.因此,这种主体密度的净减少使得超额吸附量随着温度增加而提高.图4给出了CH4和CO2在不同温度下的超额吸附量极值随着最优操作压力的变化.由图4可知,最大气体存储量随着温度的升高快速下降;同时,满足该极值目标需相应地提升压力.对于CH4和CO2的存储,较优的条件为208 K、4 MPa和298 K、6 MPa,其最大吸附量分别为10.07和14.85 mmol·g-1.
为了从微观水平上理解气体在CMK-3中存储的机理,我们在图5和6中分别给出了常温条件下CH4和CO2达到吸附平衡时的分子构型和对应的孔内流体局部密度分布.由图5可知,气体分子在CMK-3材料的表面出现大量聚集的现象,但基本上仍以单层吸附为主,同时随着压力的升高,吸附量明显增加;相同压力条件下,由于CO2具有较大的势能作用参数,CMK-3对CO2的吸附能力要强于CH4.图6中,两种物质的局部密度在r*=10时均最高,这对应着材料表面上的吸附单层,而在r*=12,15时均出现两个较弱的峰,其中前者为发生在吸附单层上面的第二层吸附,后者是发生在两相邻碳柱距离最短处因势能叠加引起的吸附层.此外,随着压力的提高,峰的强度变得更加明显.这些观察与图5中的流体分子构型是相互一致的.
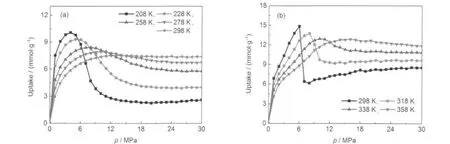
图3 GCMC模拟的甲烷与二氧化碳在不同温度下的超额吸附等温线Fig.3 Excess adsorption isotherms of methane and carbon dioxide from GCMC simulation at different temperatures(a)CH4;(b)CO2

图4 不同温度下甲烷与二氧化碳的最大超额吸附量与对应的最优压力Fig.4 Maximum adsorption amounts and the corresponding optimum pressures at different temperatures(a)CH4;(b)CO2
5.2 二元混合物的吸附分离
5.2.1 IAST方法的验证
为节省GCMC方法的计算耗时,本文选择更简单的IAST预测方法来考察二元体系的分离性质,即以双位Langmuir-Freundlich模型关联纯气体吸附的实验数据,再使用IAST计算混合物的吸附性质.我们先使用Sudibandriyo等24在活性炭上测量的纯气体和混合物吸附数据验证IAST方法的可靠性.从图7可以看出,即使压力高至13 MPa,Langmuir模型拟合和IAST的预测均与实验吻合,证明这种研究方法是可以接受的.表2给出了拟合CMK-3材料上纯气体的实验数据得到的双位Langmuir-Freundlich模型参数.由表2看出,对三种纯气体的吸附,拟合的吸附量与实验之间的平均相对偏差(ARD)均小于1%,表明回归的Langmuir模型参数可用于混合物吸附的IAST预测.
5.2.2 等摩尔比下的吸附选择性

图5 298 K下甲烷与二氧化碳在CMK-3中不同压力下的分子构型图Fig.5 Molecular configurations of methane and carbon dioxide in CMK-3 at 298 K and different pressures(1,4)1 MPa;(2,5)6 MPa;(3,6)12 MPa

图6 CMK-3材料中甲烷与二氧化碳在不同压力下的局部密度分布图Fig.6 Local density profiles of methane and carbon dioxide at different pressures in CMK-3(a)CH4;(b)CO2;ρ*:local density,r*:reduced distance from axis

图7 318.2 K下活性炭材料上绝对吸附等温线计算值和实验值比较Fig.7 Comparison of the calculated absolute adsorption amount with experimental data on dry activated carbon at 318.2 K(a)pure gases;(b)CH4-CO2mixture with CH4feed composition of 40.1%

表2 CMK-3材料中纯组分吸附的双位Langmuir-Freundlich模型参数Table 2 Parameters of dual-site Langmuir-Freundlich model for pure adsorption in CMK-3

图8298 K下IAST预测CMK-3材料上等摩尔混合物的选择性(S)Fig.8 IAST predictions for adsorption selectivity(S)of equimolar mixtures in CMK-3 at 298 K
图8为CH4-CO2、N2-CH4及N2-CO2二元混合物在常温298 K和气相等摩尔比下的吸附选择性.从图8可以看出,低压(<0.2 MPa)下的吸附选择性较高,这说明CMK-3材料中存在部分微孔的吸附作用.压力稍微增加时,微孔容积已被流体分子填充,引起吸附选择性的陡然下降.当压力高于0.5 MPa时,材料中介孔中的固体孔壁对流体的多层吸附能力较弱,而单层表面吸附对分离的贡献起主导作用,这使得吸附选择性的变化逐渐平缓.此外,对于CH4-CO2体系,其CO2吸附选择性与N2-CH4中的CH4选择性相差不大,在较高压力约为3,而CMK-3材料对N2-CO2中的CO2具有较强的优先吸附能力,其选择性稳定后保持在7.5左右.这可以根据图9中气体混合物中组分的绝对吸附等温线解释.在图9(a)与(b)中,CH4、CO2之间和N2、CH4之间的吸附等温线差距随着压力的变化总是很小,故两体系分离的选择性比较接近;而图9(c)中N2、CO2之间的吸附量差距要明显大于另外两种体系,可见CMK-3材料尤其适合分离N2-CO2体系中的CO2.尽管低压下的气体吸附选择性较高,但低压也不利于组分的存储.综合权衡,建议在4 MPa下进行吸附操作,以同时满足分离和存储的性能需求.

图9298 K下IAST预测CMK-3中等摩尔混合物的绝对吸附等温线Fig.9 IAST predictions for absolute adsorption isotherms of equimolar mixtures in CMK-3 at 298 K

图10 298 K下IAST预测CMK-3中二元混合物不同摩尔比下的吸附选择性Fig.10 IAST predictions for adsorption selectivity of binary mixtures with different molar ratios in CMK-3 at 298 K as a function of bulk pressure
5.2.3 不同摩尔比下的吸附选择性
为考察主体组成对分离性能的影响,图10给出了常温下不同气相摩尔比的二元混合物吸附选择性的变化.
由该图可知,N2-CH4体系中不同气相摩尔比的吸附曲线几乎重合,说明吸附选择性受主体相组成的影响不大.然而对于含CO2的体系,CO2选择性在压力大于2.0 MPa时随着压力和气相中CO2浓度而增加,并且压力越高现象越显著.这可根据CO2分子具有较强的四极矩特性解释.由于孔内吸附相CO2分子的密度高于主体相,在四极矩的作用下孔内CO2流体会吸引更多的主体相CO2分子进入孔内,导致孔内的吸附量和选择性提高.
6 结论
通过巨正则系综蒙特卡罗模拟提出了一种有效表征CMK-3材料结构的理论模型,并对CH4和CO2纯气体存储进行了吸附条件的优化.同时利用基于双位Langmuir-Freundlich吸附模型的理想吸附溶液理论考察了N2/CH4/CO2二元混合物在CMK-3材料上的分离性质.计算表明,CMK-3材料不仅适合于CH4和CO2气体的存储,也是一种高效分离天然气成分的吸附剂.
(1) Jun,S.;Ryoo,R.J.Am.Chem.Soc.2000,122,10712.
(2) Kyotani,T.;Sonobe,N.;Tomita,A.Nature 1988,331,331.
(3) Lee,J.;Han,S.;Hyeon,T.J.Mater.Chem.2004,14,347.
(4) Joo,S.H.;Ryoo,R.;Kruk,M.J.Phys.Chem.B.2002,106, 4640.
(5)Zhou,L.;Liu,X.W.;Wang,N.;Wang,Z.;Zhou,Y.P.Chem. Phys.Lett.2005,413,6.
(6)Xia,K.;Gao,Q.;Wu,C.;Song,S.;Ruan,M.Carbon 2007,45, 1989.
(7) Monk,J.;Singh,R.;Hung,F.J.Phys.Chem.C 2011,115,3034.
(8) Allen,M.P.;Tildesley,D.J.Computer Simulation of Liquids; Clarendon Press:Oxford,1987;pp 110-139.
(9)Peng,X.;Wang,W.C.;Xue,R.S.;Shen,Z.M.AIChE J.2006, 52,994.
(10) Myers,A.L.;Prausnitz,J.M.AIChE J.1965,11,121.
(11) Zhou,C.;Hall,F.;Gasem,K.;Robinson,J.Ind.Eng.Chem. Res.1994,33,1280.
(12) Rangarajan,B.;Lira,C.T.;Subramanian,R.AIChE J.1995,41, 838.
(13) Ottiger,S.;Pini,R.;Storti,G.;Mazzotti,M.Langmuir 2008,24, 9531.
(14)Peng,X.;Cao,D.P.;Wang,W.C.Ind.Eng.Chem.Res.2010, 49,8787.
(15)Peng,X.;Cao,D.P.;Wang,W.C.Chem.Eng.Sci.2011,66, 2266.
(16)Peng,X.;Zhou,J.;Wang,W.C.;Cao,D.P.Carbon 2010,48, 3760.
(17) Peng,X.;Cao,D.P.;Wang,W.C.Langmuir 2009,25,10863.
(18)Peng,X.;Cao,D.P.;Wang,W.C.J.Phys.Chem.C 2008,112, 13024.
(19) Peng,X.;Cao,D.P.;Zhao,J.S.Sep.Purif.Technol.2009,68, 50.
(20) Gordon,P.A.;Saeger,R.B.Ind.Eng.Chem.Res.1999,38, 4647.
(21) Cao,D.P.;Wang,W.C.;Duan,X.J.Colloid Interface Sci. 2002,254,1.
(22) Peng,X.;Zhao,J.S.;Cao,D.P.J.Colloid Interface Sci.2007, 310,391.
(23) Nguyen,T.X.;Bae,J.;Wang,Y.;Bhatia,S.K.Langmuir 2009, 25,431.
(24) Sudibandriyo,M.;Pan,Z.J.;Fitzgerald,J.E.;Robinson,R.L., Jr.;Gasem,K.A.M.Langmuir 2003,19,5323.
April 20,2011;Revised:June 8,2011;Published on Web:July 12,2011.
Adsorption and Separation of CO2/CH4/N2Binary Mixtures in an Ordered Mesoporous Carbon Material CMK-3
PENG Xuan1,*ZHANG Qin-Xue2,3CHENG Xuan3CAO Da-Peng3
(1College of Information Science and Technology,Beijing University of Chemical Technology,Beijing 100029,P.R.China;2College of Science,Beijing University of Chemical Technology,Beijing 100029,P.R.China;3Division of Molecular and Materials Simulation,State Key Laboratory of Organic-Inorganic Composites, Beijing University of Chemical Technology,Beijing 100029,P.R.China)
The adsorption and separation of natural gas in the ordered mesoporous carbon material CMK-3 was investigated by molecular simulation and adsorption theory.Grand canonical ensemble Monte Carlo (GCMC)simulations show that a maximum excess uptake of 10.07 and 14.85 mmol·g-1is obtained at the optimum temperature and pressure of 208 K,4 MPa for CH4and 298 K,6 MPa for CO2adsorption, respectively.Based on the dual-site Langmuir-Freundlich(DSLF)model,ideal adsorption solution theory (IAST)was used to predict the adsorption and separation of binary mixtures.The adsorption selectivity of SCO2/CH4is approximately the same as that ofSCH4/N2,with a value of about 3 at 298 K and 4 MPa while the highest CO2selectivity of 7.5 was found in the N2-CO2system under the same conditions.This indicates that theCMK-3 material isapromising candidate for natural gas separation.
Grand canonical ensemble Monte Carlo;Adsorption selectivity;Ideal adsorption solution theory;Methane;Carbon dioxide;Nitrogen;CMK-3
∗Corresponding author.Email:pengxuan@mail.buct.edu.cn;Tel:+86-10-64443254.
The project was supported by the National Natural Science Foundation of China(20806003).
国家自然科学基金(20806003)资助项目
O647;O641
——《势能》

