基于优化教学效果的高职数学中的引例分析与探讨

芦海英

（三亚航空旅游职业学院数学教研室，海南三亚 572000）

基于优化教学效果的高职数学中的引例分析与探讨

芦海英

（三亚航空旅游职业学院数学教研室，海南三亚 572000）

高职高等数学和经济应用数学课程中有些教学内容不易被学生理解，不适合直接阐述，而配备适当的引例既有助于新知识点的导入，又能充分体现数学产生于生产生活、用之于生产生活的特点。使用恰当的引例，不仅能提高学生的学习兴趣，调动学生的学习积极性，而且结合实例的讲解有助于学生对新课内容的理解和掌握。选取实际教学过程中两个引例，结合学生特点，尝试分析与探讨引例在教学过程中的作用。

高职数学;引例;导数定义;乘法原理;教学效果

高职数学课程一般分为两个部分，一部分是公共基础必修课微积分，另一部分是以概率论和运筹学为主要内容的文科类学生的专业基础必修课经济应用数学。这些课程基本都安排在大一，是高职学生认为最难学的一门课。

教师对于学生普遍感到吃力的科目，一方面要从学生的观念、动机、态度、行为、习惯等非智力因素入手，提高学生学习的主动性、自觉性;另一方面要从提高教师本人素质、认真研究教材和教法入手，使得学生乐于接受老师的教导、乐于接受难学的课程、乐于学习难学的内容，并且学得会、学得通、学得好。

美籍华人学习与教育大师李开复先生把学习概括为四种境界。境界一:熟能生巧，在老师指导下学习掌握课本上的基本内容，知道问题的答案;境界二:举一反三，具备思考的能力，掌握学习的方法，能够举一反三，知其然，也知其所以然;境界三:无师自通，掌握自学、自修的方法，在没有老师辅导的情况下主动自学;境界四:融会贯通，将学到的知识灵活运用于生活和工作实践，懂得做事与做人的道理。教师应主动地把对这四种境界的领会运用于日常教育和教学活动中，帮助学生提升学习效率提高学习的境界。

例如在高等数学课程中，导数是重要的学习内容，引入导数的概念时，我们不妨选择物理学中求质点在某个时刻的瞬时速度这样的问题入手。

一 高等数学关于导数定义的两个典型引例

（一）引例内容

1.变速直线运动的瞬时速度

设物体沿直线作变速运动，其规律为s=f（t），其中s表示位移，t表示时间.求物体在运动过程中某时刻t=t0的瞬时速度v（t0）.

当t在t0取得增量Δt时，则在t0到t0+Δt的时间段内，

位移的增量Δs=f（t0+Δt）－f（t0）.

即为t0到t0+Δt到这段时间内的平均速度。

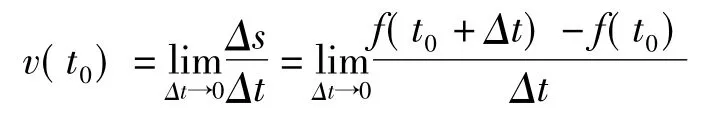
平均速度v称为位移s在t0到t0+Δt时间段内的平均变化率，而瞬时速度则称为位移s在时间t=t0的（瞬时）变化率。

2.质量非均匀分布的细杆的线密度

设细杆自一端起，长度为x的一段质量为m=f（x），求细杆在x=x0处的线密度。

有的高职高等数学教材在引入导数的定义时，使用了这两个实际问题的例子，作为讲解导数的引例。笔者根据多年教学实践的尝试和反馈，认为可以把第一个引例拿来引出导数的定义，因为学生会对高中时学习过的物理学问题产生兴趣，顺着探讨瞬时速度的思路，可以看出导数定义的必要性、实践性，从而顺利地接受与领会导数的定义。

（二）导数的定义

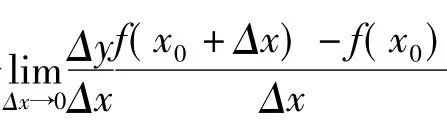
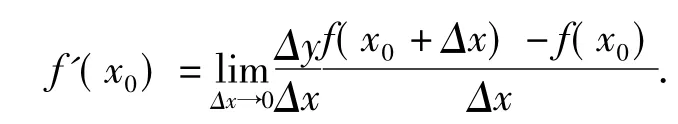
（三）教法分析与探讨

在讲授导数的定义时，如果贸然给出直接的定义，无论老师和学生都会感到抽象，甚至突兀。那么对于以上这两个典型引例，该如何使用?

为了顺利地引入导数定义，笔者建议教师选第一个典例作为引例，并且可以用教室里的讲桌作为“教具”，形象地引入变速直线运动求瞬时速度的问题。先让学生求质点在变速直线运动情况下经过整个讲桌长度时的平均速度;再看半米长度（距离）下的平均速度，再不断地缩小质点运动的距离，突出极限的思想，直到问题变为求讲桌上某个点的瞬时速度为止。这样上课容易抓住学生的注意力，顺利引入导数定义。

而后面一个典例，就放在讲完本节课之后，在小结和复习时再提出来，这样便于学生更好地理解导数的定义，还能对导数的应用产生兴趣。否则，两个引例连续使用恐怕会把学生的注意力分散到他们感到更难的物理问题，产生畏难情绪，影响我们运用引例的效果。

二 经济应用数学关于排列组合中乘法原理的典型引例

（一）三个引例

例题1:由A地到B地有3条道路，由B地到C地有2条道路，问从A地到C地共有几条道路?

例题2:由甲地到乙地的交通路线有三条，第一条路线有2班轮船，第二条路线有3班火车，第三条路线有4班汽车，那么，从甲地到乙地共有多少种不同的走法?

例题3:某同学计划早上从三亚出发，由广州转机当天飞抵哈尔滨。由三亚到广州有3班早班机，由广州到哈尔滨有2班可衔接的航班。问:该同学总共可有多少种飞行方案?

（二）乘法原理

完成一件事有n个步骤，第一个步骤有m1种方法，第二个步骤有m2种方法，…，第n个步骤有mn种方法，且只有依次完成各步骤事件才能完成，则完成这件事共有如下种方法:

A=m1×m2×…×mn

（三）教法分析与探讨

比较以上三个引例，很容易看出第一个引例字数最少，看起来语言最精炼，可是却最抽象概括，最不容易引导学生快速介入;第二个问题比第一个具体，但还是有“甲”、“乙”等这样不为学生普遍能快速介入的“障碍”。我们学院在三亚，班级里有些哈尔滨同学，如何在假期前购买机票是他们最关注的问题。于是乘法原理的引例就变成了动员全班同学帮助家乡远在哈尔滨的同学解决假期购票的问题，很能引起学生的学习兴趣，调动学习积极性，在教学实践中起到良好的效果。

综上，数学基础普遍较差的高职学生的抽象思维能力、逻辑推理能力远不如形象思维能力发达，在高职数学学科备课过程中，在引入新知识的时候，应注意以下几点:第一，尽可能避免连续给出过多的有难度的问题，以保护学生的学习积极性;第二，避免抽象的符号直接介入问题，而尽可能把问题转化为与他们密切相关的实际问题，引发他们的兴趣与思考;第三，为了培养和提高学生的抽象思维能力、逻辑推理能力，在学生理解和掌握了对于新知识点的概念、原理和方法后，再由特殊到一般，由局部到整体地推广学习内容，这样就会收到事半功倍的效果。

［1］李开复.做最好的自己［M］.北京:人民出版社，2005.

［2］张庆林.高效率教学［M］.北京:人民教育出版社，2002.

［3］珍妮特·沃斯，戈登·德莱顿.学习的革命［M］.上海:三联出版社.

The Case Analysis and Discussion Based on Optimizing Teaching Performance in Vocational Mathematics

LU Hai－ying
（Mathematics Department，Sanya Aviation＆Tourism College，Sanya 572000，China）

It is difficult for students to appreciate some materials of mathematic course in vocational advanced mathematics and economic applied mathematics.Therefore，some cases will help introduce the new knowledge and indicate that mathematics come from and serve our daily life.Proper cases will improve students’learning interest and activate their enthusiasm.At the same time，explanations combined with cases will facilitate the students to understand and master new points.The paper tries to analyze and discuss the role of cases in teaching by choosing two cases in teaching process with students’characteristics into account.

Vocational mathematics;Case;Derivative definition;Multiply principle;Teaching performance

G712、O13

A

1009－9743（2011）04－0145－03

2011－11－22

芦海英（1969－），女，汉族，吉林辽源人。三亚航空旅游职业学院基础教学部数学教研室讲师。主要研究方向:高等数学、经济应用数学。容易看出，当Δt越小时，平均速度将越接近瞬时速度，当Δt无限趋近于零时，平均速度也将无限趋近瞬时速度。为此，瞬时速度定义为平均速度当 Δt→0时的极限，即

（责任编辑:于保霞）