超级画板在高中数学概念教学中的应用
杨 黎,雷吉红
(海南师范大学初等教育学院,海南海口 571158)
超级画板在高中数学概念教学中的应用
杨 黎,雷吉红
(海南师范大学初等教育学院,海南海口 571158)
概念是数学中的基本内容。介绍超级画板的特点,结合教学设计案例从概念的形成与概念的同化两个方面探究了超级画板在数学概念教学方面的应用。
超级画板;数学概念;概念的形成;概念的同化
超级画板能满足数学教学和学习的需求,能够用于课堂教学、解题、复习知识、数学课外活动等各种环境中,是一款智能教育软件,在数学教学中具有独特的优点[1]。数学概念是数学中的基本内容,学生掌握数学概念不仅仅是能够用自然语言来表述数学概念,更重要的是能够理解和掌握并应用数学概念。概念的形成与概念的同化是概念获得的两种方式。依据陈琦和刘儒德的观点[2](p240-241),笔者认为,概念的形成是学生对同类事物的各种实例进行分析比较,发现这类事物共同本质属性的过程;而概念的同化是教师直接用概念的方式向学生展示一类事物的本质属性,学生利用其认知结构中已有的概念理解新概念的过程。同样,数学概念也有数学概念的形成与数学概念的同化两种获得方式。应用超级画板进行数学概念的教学,把抽象的数学概念变成具体直观的知识,使学生在理解、掌握数学概念的基础上准确地运用数学概念。针对这两种数学概念的获得方式,笔者设计了两种关于数学概念的教学方式。
一数学概念的形成的教学设计
根据新课程理念,数学概念的形成采取如下的教学方法进行教学:“第一步,向学生出示概念的正例和反例;第二步,要求学生总结归纳,得出概念;第三步,呈现例子以巩固概念,这种方式被称之为:例子——规则——例子”。与之相应的教学流程如图1:

图1
(一)案例:函数单调性定义的教学设计
设计意图:函数是高中数学必修1的内容。函数单调性是第一个函数性质,也是第一个用数学符号语言来刻画的概念,教学可借助超级画板展现函数单调性的实际生活情境,教师引导学生从自然语言过渡到图形语言,再过渡到数学语言,从而总结归纳出函数单调性概念。
具体设计:
1.创设情境,提出问题
教师出示:某市一天的气温变化数据表,给出了具有代表性的几组数据(如图2),在超级画板中用函数曲线表示该市的气温变化图(如图3)。教师提问:观察这个气温变化图,回答气温在这一天内的变化情况;怎样用数学语言刻画这一天内“随时间的增长,气温逐渐升高或降低”这一特征?教师引导学生观察函数图,启发学生思考,引导学生从函数图像中获得尽可能多的信息,其中有两方面的信息要注意:一是当天的最高温度、最低温度以及何时到达的;二是某些时段温度升高,某些时段温度降低。

图2

图4
到目前为止,教师已经引导学生从自然语言符号和图形语言符号,即“形”的角度认识了函数单调性,接下来应该引导学生从数学符号语言,即“数”的角度来刻画函数的单调性定义。学生先独自思考,再分小组交流谈论。教师引导学生总结归纳得出函数单调性(增函数)的定义。最后,教师引导学生总结减函数的定义。

图3
2.探索新知,归纳小结,形成概念
教师在超级画板中画出两个具体函数图像(图4、图5)。教师提问:函数图像有什么共同特征?并引导学生讨论下列问题:在超级画板的界面中,从左向右,函数图像是如何变化的?随着x的增大,y如何变化?让学生在函数图像上任意作一点A(x1,y1),引导学生在超级画板的界面上由左向右移动点A,在测量中观察点A纵坐标的变化。
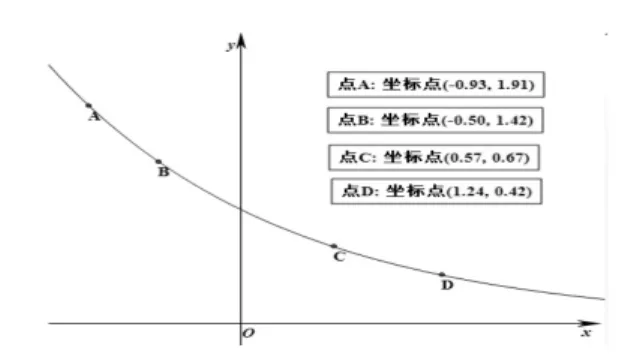
图5
3.利用实例深化概念
让学生在理解函数单调性定义的基础上判断出函数y=3x+1(图6),y=(图 7),y=x2(图8)的单调性,提醒学生注意有些函数的单调性是对定义域内某个区间而言的。
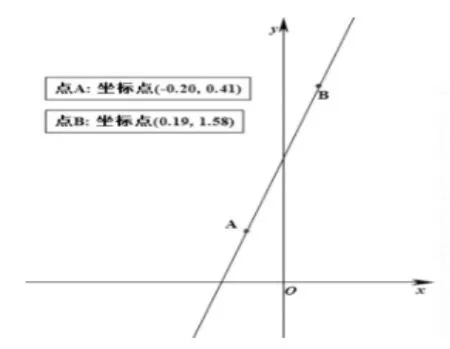
图6

图7
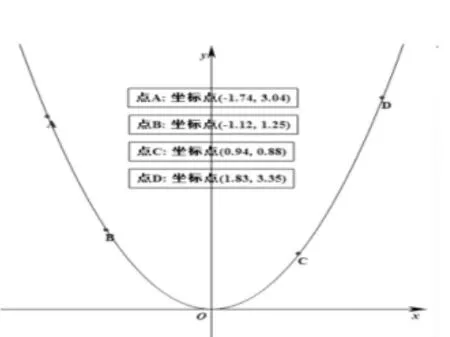
图8
设计分析:函数单调性学习应先引导学生接触生活实际的函数图像,进而观察数学函数的图像,通过归纳抽象出数学符号的概念。借助超级画板可以直观形象地呈现教学所需的函数图像,让学生更加形象直观地理解和接受函数单调性的定义。
二 数学概念的同化的教学设计
上面分析了通过概念的形成来进行数学概念教学的流程和案例,对于数学概念的同化要采取不同的教学方法来进行数学概念的教学:“第一步,教师给学生一个概念;第二步,要求学生判断正例和反例;第三步,引导学生分析上述例子是如何代表这一概念的,这种方式称之为规则——例子——规则”。与之相应的教学流程如图9:

图9
(一)案例:异面直线的教学设计
设计意图:异面直线是高中数学必修2的内容。高中学生的心智发育程度决定了他们对空间几何存在一定的认知困难。在进行异面直线的教学时,教师应先从学生生活中的实例引入,再告知学生异面直线的实例与异面直线的关键特征,然后引导学生找出超级画板界面中的直观图形(长方体)中的异面直线,不断地改变长方体的摆放位置,在寻找判断中理解并掌握异面直线的概念。
具体设计:
1.出示定义,告知关键特征
教师引导学生观察教室中模型的点、线、面,以及引导学生观察超级画板中长方体(图10)的点、线、面,然后告知学生异面直线的定义:“不同在任何一个平面内的两条直线叫做异面直线”。关键特征:既不平行,也不相交。

图10

图11

图12

图13
2.提出问题,观察探究,类比分析
教师引导学生观察超级画板中的图形,提问:在长方体中,下列哪些直线平行?哪些直线相交?另外,下列两组直线AA’与BC、A’B与B’C是否平行?是否相交?是否为异面直线?教师要求学生作出回答,根据回答的情况在超级画板的界面上不断地转动长方体到不同的位置(图11、图12、图13),让学生反复观察长方体各条边的关系,尤其这两组直线的位置关系。
3.获得概念,深化概念
在讨论得出一定结论后,教师引导学生总结空间两条直线的关系和空间内两条直线位置关系的分类(分别从有无公共点的角度和是否共面的角度),让学生自己总结出异面直线不同于平行直线、相交直线的特征,促使学生获得异面直线的概念。最后,要求学生在长方体中找出其他的异面直线。
设计分析:立体几何是培养学生空间想像能力的重要内容,掌握异面直线的概念是理解立体几何中其他一些概念的基础。此上述教学设计中直观形象的长方体能够帮助学生以概念同化的形式获得异面直线的概念:首先学生从教师所给的定义和特征中了解异面直线关键属性——不共面;然后在实例中与平行直线、相交直线分类比较,进一步概括出异面直线的概念,最后由学生在超级画板界面中展示的不同摆放位置的长方体中找出其们异面直线,是对异面直线概念的巩固和深化。
三结语
超级画板充分体现了数形结合的数学思想,符合很多数学概念教学要求,特别是在图形的可视化处理和动态演示方面,均起到了促进学生更好地掌握数学概念,提高教学质量的作用。以上只是通过实例简单描述超级画板在数学概念教学中的辅助作用。然而,任何教学技术都只是一种教学工具,一种教学手段,应该服从教学目标,不可过分依赖。在借助超级画板进行教学的过程中,要注意对学生能力的培养,而不是增加学生的学习负担。
[1]张景中.超级画板在高中数学教学中的应用[J].高等函授学报(自然科学版),2008(22).
[2]陈琦,刘儒德.教育心理学[M].北京:高等教育出版社.2005.
[3]闫喜玲.信息技术与高中数学课程整合下的教学设计研究[D].首都师范大学.2009.
[4]何克抗.信息技术与课程深层次整合的理论与方法(上)[J].电化教育研究,2005(1).
[5]杨世军.超级画板与初中数学课程整合的教学研究[D].华中师范大学学位论文,2008.
[6]尚晓青.DGS技术与初中几何教学整合研究[D].西南大学学位论文.2008.
Application of Super Sketchpad in Teaching Mathematical Concepts in High School
YANG Li,LEI Ji- hong
(Department of Elementary Education,Hainan Normal University,Haikou 571158,China)
Mathematical concept is the basic content in mathematics.This article describes?the characteristics of the Super Sketchpad,with cases of instructional design from the assimilation and conformation of concepts in teaching mathematical concepts.
Super Sketchpad;Mathematical concept;Assimilation of concept;Conformation of concept
G 633.6
A
1009-9743(2011)04-0141-04
2011-12-01
杨黎(1986-),女,汉族,湖北襄阳人。海南师范大学课程与教学论专业在读硕士。主要研究方向:数学课程与教学论;雷吉红(1985-),女,苗族,贵州紫云人。海南师范大学课程与教学论专业在读硕士。主要研究方向:教学论。
(责任编辑:于保霞)

