盾构刀盘掘进载荷的数值模拟
苏翠侠,王燕群,蔡宗熙,亢一澜,黄 田
(天津大学机械工程学院,天津 300072)
盾构掘进机是目前隧道掘进的专门工程机械,被广泛用于地下交通、运输管道等隧道工程建设.施工过程中刀盘系统与土体相互耦合作用,并受到地质等因素的影响,刀盘载荷十分复杂,因此,研究刀盘载荷分布规律,分析刀盘系统与土体的适应性,对优化刀盘拓扑结构、提高施工效率具有指导意义.
盾构刀盘的作业空间处于地表以下,属于封闭式作业且工作环境复杂多变,无法直接观测刀盘在掘进过程中的载荷分布,因此目前针对刀盘载荷的研究较少.以往对盾构刀盘的研究主要集中在简化理论与模型实验等方面:简化理论方面主要是通过分析各种刀具的切削机理[1]推导盾构掘进所需总载荷[2],进而分析刀盘一般设计理论及其影响因素[3];模型实验方面主要是通过制造等比例小型简化刀盘,进行土箱实验分析不同地质条件和掘进参数对掘进推力、扭矩等载荷的影响[4];另外一种方法是结合大量的实际工程的施工数据建立刀盘掘进参数的经验公式[5],总结各种刀具破坏形式及其检测方法[6],对影响刀盘掘进效率的因素进行分析及改进.
近年来随着数值技术的发展,有限元法为研究盾构刀盘载荷提供了一种新工具.盾构刀盘的载荷主要由刀盘与土体相互作用产生,刀盘掘进过程本质上可以视为动态的切削问题.采用有限元法从切削角度分析刀盘掘进必须考虑以下几个方面的问题:有限元模型的建立、土体本构的选择和切屑分离的模拟.
创建适合的模型是数值仿真的首要问题,在满足计算精度要求的基础上应对模型进行合理的简化以节约计算成本.
土体本构的选择直接影响计算结果,近年来土力学的发展较为成熟,已经有越来越多的适合描述不同岩土特性的本构模型被提出,目前应用较多的岩土模型主要有Duncan-Chang 双曲线模型、Drucker-Prager非线性弹塑性模型、Cam-Clay 模型、黏弹塑性盖帽模型等,研究结果表明它们大都能够给出满足适当精度要求的结果.
有限元模拟切屑分离的方法有很多,根据分离依据可以分为两类:基于应力、应变能密度或有效塑性应变等[7]物理量的物理准则和基于距离等几何尺寸的几何准则[8].具体实现方法包括单元移除、节点脱粘、节点分离等.切削仿真中上述切削分离方法选取不当经常引起网格畸变导致计算不收敛,采用离散元和有限元结合[9]、ALE 方法[10]、流固耦合、自适应网格划分技术[11]等方法在一定程度上能够描述网格大变形问题,但在应用中存在各自的局限性.
以往的研究或着眼于静力分析或将刀盘简化为简单的柱形刚体,都忽略了切削过程,相关的耕耘机刀具与土壤的切削仿真[12]以及金属切削仿真[8]研究为有限元分析盾构刀盘切削问题提供了一定的参考.Shen 等[10]在此基础上将有限元分析土壤切削的方法应用于盾构刀盘掘进分析,针对盾构刀盘建立了一个简化三维模型,实现了刀盘掘进仿真.Shen 采用的Ls-Dyna 中的MAT147 材料模型对标准的摩尔-库伦准则进行了修正,确定了与压力相关的峰值剪切强度,并提出了将ALE 方法应用于刀盘-土体切削,从流体-固体耦合的角度处理了刀盘-土体的相互作用,解决了切削引起的土体大变形问题.但是一般来说,采用ALE、流固耦合等方法计算时间较长,占用了大量的计算资源;且此类方法研究的刀盘模型都比较简单,给出的关于刀盘载荷的信息不是特别丰富.正是由于这些因素的存在,至今未能得到刀盘在掘进过程中的更多的有效的载荷信息.
针对盾构刀盘掘进载荷问题,笔者采用有限元软件ABAQUS/Explicit 进行了数值模拟仿真计算,建立了模拟盾构刀盘掘进过程中连续切削土体的三维动态仿真模型.在计算中采用了扩展的 Ducker-Prager 非线性弹塑性的材料本构关系,应用了具有单元删除功能的损伤失效准则,实现了对盾构刀盘掘进过程中的土体切屑分离的数值模拟.最后,本文基于三维仿真结果,讨论了盾构刀盘动态掘进过程中的切削载荷沿刀盘半径分布、随时间变化规律以及刀盘系统切削土体所受到的扭矩.
1 三维动态仿真模型
隧道掘进是一个复杂的施工过程,它对周围环境扰动较大,且由于盾构装备结构的复杂性,机械本身和施工环境影响盾构掘进过程的因素也很多.本文重点研究盾构刀盘掘进过程中的载荷分布,因此有限元建模包括了盾构机刀盘与正前方相互接触区域的土体,以此作为盾构刀盘系统三维动态仿真整体模型.
1.1 模型介绍
以天津地铁工程中的土压平衡盾构刀盘作为原型.刀盘直径为6.4,m,根据刀盘的二维设计图纸,经适当简化建立相应的三维有限元模型.简化包括删除不影响结构强度的螺栓孔、泡沫注入口、倒角、拐角等特征.刀盘原型以切刀为主,由于面板相邻切刀的刀间距较小,因此对切刀进行简化,在保证刀具前角及后角不变的基础上在切刀布刀位置以连续刀刃代替分散的切刀,如图1 所示.
在刀盘正前方加入圆柱形的土体模型,形成刀盘切削土体的整体有限元分析模型,如图2 所示.整个有限元模型采用六面体8 节点实体单元划分网格,模型节点总数为104,364,单元总数为80,828.为得到较好的计算精度并提高计算效率,将仿真过程中与刀盘直接接触的被切削的部分土体网格加密,未与刀盘直接作用的土体网格适当加大.
盾构刀盘的材料为Q345 钢.弹性模量E= 210 GPa ,密度 ρ=7 850 kg m3,泊松比ν= 0.26.土体取天津地区的黏性软土,主要材料参数为:弹性模量E= 7.098 MPa ,密度ρ=1 850 kg m3,泊松比ν= 0.3,内聚力9.5 kPa ,摩擦角23°.
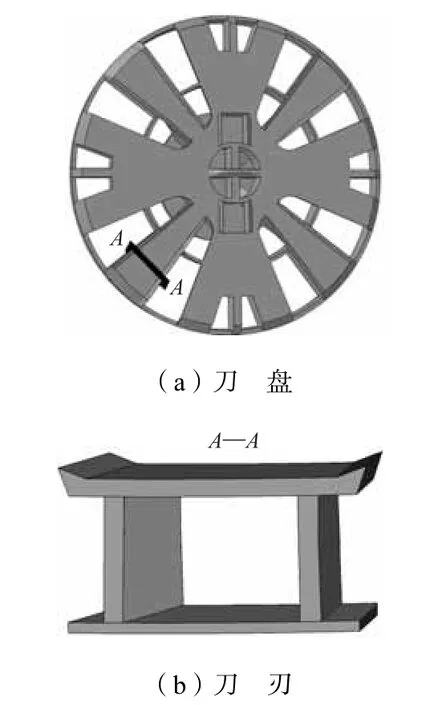
图1 盾构刀盘模型Fig.1 Model of cutterhead
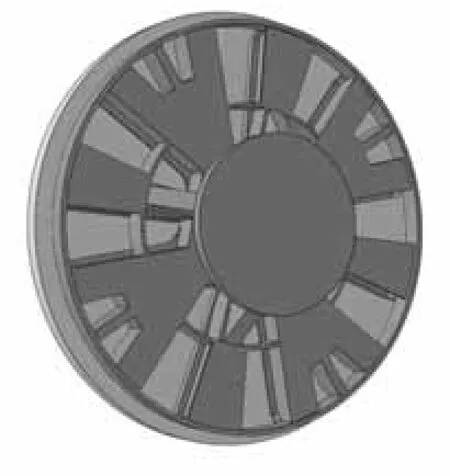
图2 刀盘与土体模型Fig.2 Model of cutterhead and soil
在实际施工中,盾构刀盘旋转切割土体的同时受到后方液压千斤顶的顶进作用,以缓慢速度向前推进.鉴于本文中只是初步模拟盾构刀盘切削土体过程,综合以上各点,对实际分析模型进行相应考虑和简化,施加的载荷和位移边界条件可总结如下.
(1) 初始状态盾构刀盘与土体即将接触.
(2) 刀盘的旋转速度为1 r min .
(3) 刀盘的推进速度为40 mm min .
(4) 仿真时间为30,s,即盾构刀盘环向切割土体1/2 圈.转速和推进速度在前5,s 以光滑加载方式由零增加到最终值,随后保持不变.
(5) 约束土体模型外边界的位移自由度,保持待开挖表面为自由表面.
(6) 利用非光滑接触条件模拟盾构刀盘和土壤之间的相互作用.
1.2 土体模型
掘进过程中土体材料特性直接影响刀盘载荷分布.盾构掘进施工面临的地质情况复杂多变,应根据实际工程采用与之相适应的本构模型.本文采用了文献[13]的扩展Drucker-Prager 非线性弹塑性本构.
与常用的Tresca 屈服条件、von Mises 屈服条件和双剪应力屈服条件相比,Drucker-Prager 模型不仅在屈服准则中引入了中间主应力对材料屈服面的影响,同时考虑了静水压力对材料屈服面的影响.Mohr-Coulomb 屈服条件虽然应用比较广泛,但它的屈服面在Π平面上表现为一个不等角的等边六边形,具有棱角奇异性,应用于数值计算时会带来较大的困难.Drucker-Prager 屈服准则克服了这一缺点,并且选择适当的材料常数可以与 Coulomb 模型相匹配.本文采用的土体模型是对Drucker-Prager 准则加以改进的扩展Drucker-Prager 准则,即
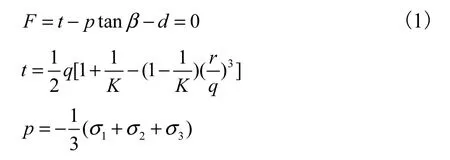
式中:r 为偏应力第三应力不变量;K为单轴拉伸屈服应力与单轴压缩屈服应力比值;d为凝聚力;β为材料摩擦角;q 为Mises 等效应力;p为平均压应力;σ1、σ2和σ3分别为3 个方向的主应力.实际计算时要考虑土体围压的影响.
在传统的Drucker-Prager 准则基础上,考虑拉伸、压缩环境不同对屈服面的影响引入参数K,如图3 所示,当材料的拉伸强度与压缩强度相同时K= 1,t=q,即退化为传统的Drucker-Prager 准则.流动法则采用关联流动法则.
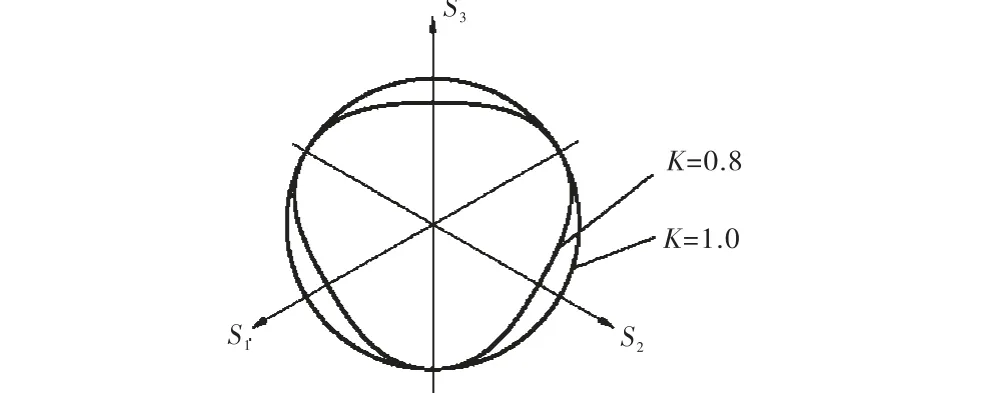
图3 偏平面内线性扩展Drucker-Prager 屈服准则Fig.3 Typical yield surfaces of Drucker-Prager model in the deviatoric plane
1.3 包含单元删除功能的单元损伤失效模型
土体从屈服到破坏是一个连续的过程,以往的仿真研究中对土体切屑的处理一般认为屈服即破坏,即以土体屈服点的各种特征判断切屑分离、形成准则,而忽略了切削形成到分离这一过程.引用的包含单元删除功能的单元损伤失效模型则描述了材料从屈服发展到破坏响应过程.
单元删除功能是为了克服有限元本身缺陷的一种方法.有限元是基于连续介质力学原理的,即物质域在空间中连续,因此单元本身是不会消失的.而在实际情况中,损伤断裂的存在必会使得一些单元消失或完全的失效,为了能够模拟这种情况,有限元中引入了单元删除功能.单元损伤失效是基于断裂力学描述损伤对于材料破坏的影响而提出的,假设基于特定本构关系的单元材料在达到强度极限以后,材料刚度按照一定的规律逐渐衰减到零,单元完全丧失承载能力并退出整体模型的计算.如图4 所示,单元损伤失效过程包含3 个部分:单元失效前的材料响应AB段、初始破坏点B点(由初始损伤准则判定)和损伤演变规律BC段.
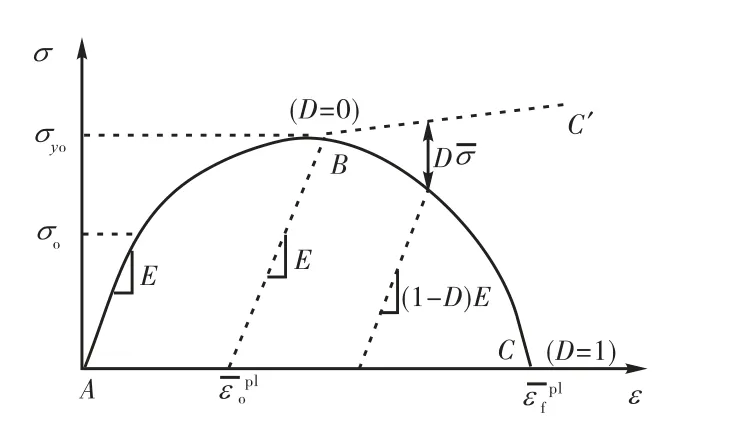
图4 损伤失效模型应力-应变响应曲线Fig.4 Stress-strain curve with progressive damage degradation
如图4 所示,AB段材料处于弹塑性变形阶段,材料达到强度极限后,由单元积分点的等效塑性应变建立基于剪切失效准则的初始损伤准则,即假设材料在开始破坏之前的塑性应变为,定义一个描述塑性变形随等效塑性应变递增的状态变量为

式中:θs为剪应力率;τmax为最大剪应力;为应变率.
当ω s达到1 时,达到初始破坏点B.
材料达到初始破坏点后刚度开始衰减直至丧失承载能力,损伤演变规律描述了材料刚度衰减规律(图4 中BC段).引入损伤变量D(当D= 1时,材料完全失去承载能力),初始损伤发生后任意时刻材料的应力张量

式中为当前时刻不考虑失效时(图4 中BC′段)的有效应力张量.
本文采用位移控制损伤定义材料损伤演变规律.如上所述,当材料达到剪切破坏准则以后,有效塑性位移由式(3)所示的损伤演变方程决定.假设材料完全失效时(如图4 中C点)的有效塑性位移为,定义

式中L 为单元特征长度.
单元完全失效后(图4 中,C点),随即被从模型中删除不再显示,就像失效单元已经消失了一样.基于连续介质力学原理,有限元实际处理单元删除问题时,材料完全失效时单元并未消失,只是失效单元刚度乘了一个极小的数值后接近于零,使得失效单元退出对有限元整体模型的贡献.
2 盾构刀盘掘进三维仿真结果分析
2.1 刀盘刀刃切向切削力分布规律
由刀盘结构可以看出刀具始终高于刀盘面板.在掘进过程中,刀具首先与掌子面接触并成为整个切削过程的主体,也是整个刀盘切削载荷的主要承力部位.刀具与土体相互作用使得刀具受到垂直于前刃面的作用力,将此作用力按照刀具的切削轨迹沿切向及法向分解即得到切向破坏土体所需要的切削力和法向与土体挤压的作用力.以下就盾构刀盘刀刃部分在掘进过程的数值计算结果进行分析.
图5所示为R= 2.8 m 处刀刃切向切削力在掘进过程中随掘进时间t的变化曲线,其中R为刀刃所在位置的半径.从图中可以看出,在掘进初始阶段,刀盘刀刃与土体逐渐接触,切削力迅速增大,经过一段时间进入稳定掘进状态,切削力也趋于稳定.分析刀具切削路径,由于沿径向分布的刀刃各部分切削形式相同、切削路径一致,刀刃各部分的切向切削力随时间变化规律一致.
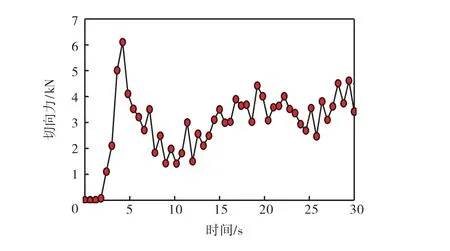
图5 R=2.8 m 处刀刃切向切削力随时间的变化Fig.5 Change of tangential force of simplified cutter when R=2.8 m
图6 所示为掘进过程中 3.6 st= 时盾构刀盘刀刃切向切削力沿半径方向的分布.可以看出:随着半径增大,刀刃切向切削力逐渐增大.此时为掘进初始阶段,刀盘缓慢加载,刀盘刀刃与土体逐渐接触,土体单元还未出现失效.由于距刀盘中心的距离不同,刀刃各部分的切削进程也不同,距离刀盘中心较远的刀刃切削力更快地达到稳定值.此时盾构刀盘刀刃切削力与布刀位置有关.
图7给出了掘进过程中 25 st= 时盾构刀盘刀刃切向切削力沿半径方向的分布.可以看出,刀刃切向切削力沿半径方向分布变化较小.掘进过程达到稳定阶段后,刀刃各部分切削形式相同、切削路径一致,切削力趋于稳定,切向切削力沿半径变化较为平缓;且随时间变化较小.距离刀盘中心较近的刀刃由于受中心刀的影响,同时切向线速度较低,切削力相对较小.刀盘面板在半径为2.0,m 处含有环形筋板结构,由于筋板的影响,刀刃刀角大于实际切刀刀角,该处切向力较小.

图6 t=3.6 s 时刀刃切向切削力沿半径方向的分布Fig.6 Tangential force distribution of simplified cutter in the radial direction when t=3.6 s
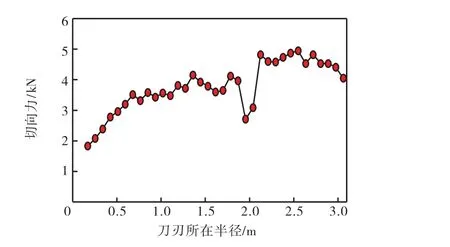
图7 t=25 s 时刀刃切向切削力沿半径方向的分布Fig.7 Tangential force distribution of simplified cutter in the radial direction when t=25 s
2.2 刀盘刀刃法向挤压力分布规律
图8给出了掘进过程中刀盘刀刃法向挤压力合力随时间变化曲线.可以看出,刀刃法向合力在刀盘与土接触后迅速增大到稳定值.刀盘转动1/4 转后首层单元失效完成1 个切削周期,18 s 时刀刃与重新形成的掌子面接触开始第2 个切削周期.刀盘刀刃法向合力具有周期稳定性.

图8 掘进过程刀盘刀刃切削力法向合力随时间的变化Fig.8 Change of total normal force of simplified cutter during excavation
图9给出了掘进初始阶段 3.6 st= 时刀刃法向力沿半径的分布曲线.可以看出:随着半径增大,刀刃法向力逐渐增大.由刀盘结构可以看出掘进初始阶段,刀盘面板与掌子面之间存在空隙,凸出面板许多的中心刀将首先与土体接触并成为面板与掌子面相互作用法向力的主要承重部位,受中心刀的影响,刀盘与掌子面发生变形.随着刀盘继续推进距中心刀较远的刀刃先于距中心刀较近的刀刃接触土体,导致同一时刻刀刃法向力随半径增大.
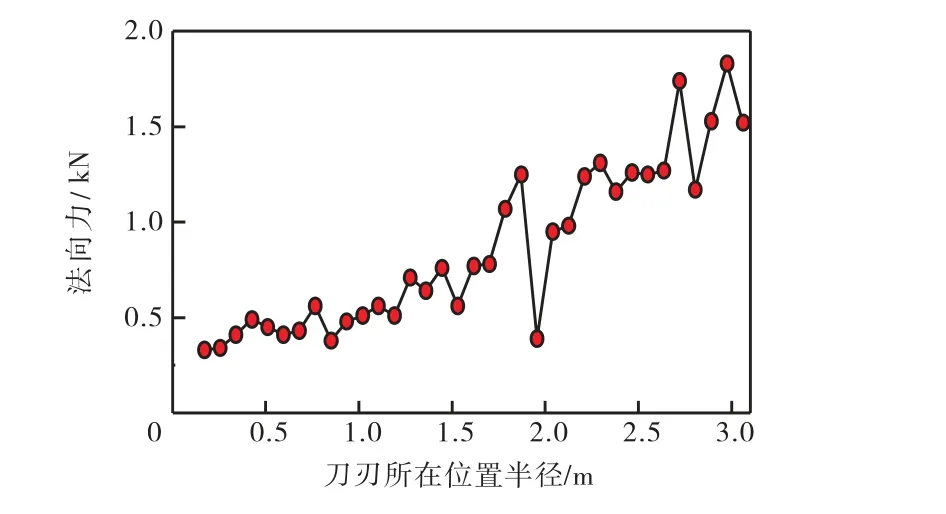
图9 t=3.6 s 时刀刃法向力沿半径的分布Fig.9 Normal force distribution of simplified cutter in the radial direction when t=3.6 s
图10给出了掘进过程中 25 st= 时刀刃法向力沿半径的分布曲线.可以看出:刀刃法向力沿半径方向分布变化不大.与刀刃切向力同理,掘进稳定后刀刃各部分切削环境相似、切削形式相同,法向切削力在掘进稳定后与布刀位置无关.由于筋板处刀刃刀角增大,导致法向力在半径为2.0,m 处数值略有减小.

图10 t=25 s 时刀刃法向力沿半径的分布Fig.10 Normal force distribution of simplified cutter in the radial direction when t=25 s
2.3 刀盘掘进过程扭矩变化
将刀盘上与土体相互作用产生的力沿面板面内对刀盘中心取矩即得到刀盘掘进过程中克服土体阻力所需的扭矩.图11 给出了有限元掘进仿真过程中整个盾构刀盘受到的扭矩随时间的变化情况.可以看出:扭矩在掘进初始时刻随时间迅速增大到稳定值,随后保持不变.盾构实际施工过程中,当掘进过程稳定后,切削状态达到平衡,各掘进参量在整个掘进过程中保持稳定不变.图11 给出的扭矩随时间的变化与实际施工情况相符,反映了刀盘扭矩的变化规律.
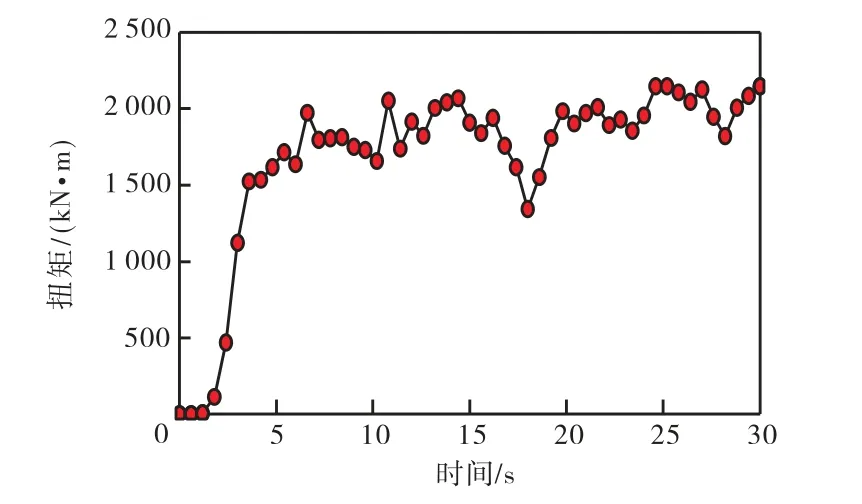
图11 掘进过程中刀盘扭矩随时间的变化Fig.11 Change of torque of cutterhead during excavation
2.4 刀盘面板应力分布
图12给出了掘进过程稳定后(25 st = 时)刀盘面板应力分布.可以看出:刀盘整体受力均匀,高应力区主要集中在刀刃和开口处以及刀盘筋板与面板连接处.最大应力为56,MPa,出现在筋板与面板连接处.计算结果表明,随着刀盘掘进仿真趋于稳定,刀盘自身的受力情况也逐渐稳定,刀盘面板大部分区域应力水平低于20,MPa,远远小于强度极限.
以往有限元研究刀盘载荷问题时,通常是直接将均布载荷施加在刀盘面板上,将动态问题简化为静力分析,忽略了刀盘与土体的相互作用.本文模型较以往的相关研究的有限元简化模型更接近真实刀盘,并考虑了刀盘切削土体的动态效应,因此本文中给出的盾构刀盘在掘进仿真过程中的载荷分布与实际情况更加接近.

图12 t=25,s时刀盘有效应力分布Fig.12 Nephogram of stress pattern of cutterhead when t=25,s
3 结 论
(1) 实现了盾构刀盘掘进过程的直接数值模拟.利用包含单元删除功能的损伤失效模型模拟土体从屈服到破坏这一连续性过程,不仅从形态上反映了盾构刀盘切削土体的物理现象,且单元失效后退出计算时的变形相对较小,在一定程度上避免了网格出现极大的扭曲和畸变.与ALE、流固耦合等技术相比,本文方法求解方程规模小,节省了计算资源.
(2) 得到了刀盘切削载荷随时间变化规律及沿径向分布规律.掘进过程中,盾构刀盘的切削载荷主要集中在刀具上.在掘进初始阶段,由于中心刀与刀刃切削进程的影响,刀刃法向挤压力和切向切削力沿径向递增且变化较大;而在掘进稳定后,则沿半径变化较小.
(3) 得到了刀盘切削扭矩随时间变化规律.在掘进初始阶段,盾构刀盘缓慢加载,刀盘与土体逐渐接触,刀盘切削力矩逐渐增加.掘进稳定后,刀盘的刀刃切削及受力状态也趋于稳定,扭矩增大到最大值后保持稳定不变.总体变化趋势与实际相符.
[1]宋克志,潘爱国. 盾构切削刀具的工作原理分析[J].建筑机械,2007(3):74-76.Song Kezhi,Pan Aiguo. Operation principle analysis of cutting tools on shield[J].Construction Machinery,2007(3):74-76(in Chinese).
[2]管会生. 盾构刀盘扭矩估算的理论模型[J]. 西南交通大学学报,2008,43(2):213-217.Guan Huisheng. Theoretical model for estimation of cutterhead torque in shield tunneling[J].Journal of Southwest Jiaotong University,2008,43(2):213-217(in Chinese).
[3][日]土木学会. 隧道标准规范(盾构篇)及解说[M].宋 伟,译. 北京:中国建筑工业出版社,2001.Japan Society of Civil Engineers.Japanese Standard for Shield Tunneling[M]. Song Wei,Trans. Beijing:China Architectural Industry Press,2001(in Chinese).
[4]朱合华,徐前卫,郑七振,等. 软土地层土压平衡盾构施工参数的模型试验研究[J]. 工木工程学报,2007,40(9):87-94.Zhu Hehua,Xu Qianwei,Zheng Qizheng,et al. Experimental study on the working parameters of EPB shield tunneling in soft ground[J].China Civil Engineering Journal,2007,40(9):87-94(in Chinese).
[5]Bernhard Maidl,Martin Herrenknecht,Lothar Nheuser.Mechanized Shield Tunneling[M]. Berlin:Ernst and Sohn,1996.
[6]赵维刚,刘明月,杜彦良,等. 全断面隧道掘进机刀具异常磨损的识别分析[J]. 中国机械工程,2007,18(2):150-153.Zhao Weigang,Liu Mingyue,Du Yanliang,et al. Abnormal cutter wear recognition of full face tunnel boring machine(TBM)[J].China Mechanical Engineering,2007,18(2):150-153(in Chinese).
[7]Carroll J T,Strenkowski J S. Finite element models of orthogonal cutting with application to single point dia-mond turning [J].International Journal of Mechanical Sciences,1988(11):899-920.
[8]王 霄,卢树斌,高传玉. 金属切削加工有限元模拟技术的研究[J]. 煤矿机械,2006,27(11):51-54.Wang Xiao,Lu Shubin,Gao Chuanyu. Research on finite element modeling techniques of metal cutting[J].Coal Mine Machinery,2006,27(11):51-54(in Chinese).
[9]Onate E,Rojek J. Combination of discrete element and finite element methods for dynamic analysis of geomechanics problems[J].Computer Methods in Applied Mechanics and Engineering,2004,193(27/28/29):3087-3128.
[10]Shen J Q,Jin X L,Li Y,et al. Numerical simulation of cutterhead and soil interaction in slurry shield tunneling[J].Engineering Computations,2009,26(7/8):985-1005.
[11]Susila E,Hryciw R D. Large displacement FEM modeling of the cone penetration test(CPT)in normally consolidated sand[J].International Journal for Numerical and Analytical Methods in Geomechanics, 2003 ,27(7):585-602.
[12]Mootaz Abo-Elnor,Hamilton R,Boyleb J T. 3D dynamic analysis of soil-tool interaction using the finite element method[J].Journal of Terramechanics,2003,40(1):51-62.
[13]Hibbitt,Karlsson and Sorensen,Inc.ABAQUS Analysis User’s Manual Help Online[M]. USA:SIMULIA,2005.
——分清“主”和“次”

