垂直上升管道内气液两相细泡流涡街特性的数值仿真

孙宏军，刘 畅

(1. 天津大学电气与自动化工程学院天津市过程检测与控制重点实验室，天津 300072；2. 北京航空航天大学仪器科学与光电工程学院，北京 100191)

气液两相流广泛存在于自然界和工业生产中，流过绕流物体时，一定条件下会产生漩涡，并引起振动．工业设备中，气液两相流钝体绕流产生的振动一方面具有破坏性[1]，另一方面隐含着流动信息．因此，充分认识气液两相流钝体绕流的规律和流场分布特性，并通过电学手段表征，可以为工业设备的抗振设计以及气液两相流体的流动参数测量提供理论依据．Hulin 等[2]和林宗虎等[3]通过实验研究了气液两相流钝体绕流的一些特性．文献[2]得出当来流含气率小于10%时涡街是稳定的结论，文献[3]在垂直上升和垂直下降2 个流向分析了漩涡脱落特性．但气液两相流流场复杂，真实流动状态不易检测，通过实验无法研究流场各个位置上的基本物理量(速度、压力、温度、组分等)的分布，以及这些物理量随时间的变化情况；因此，利用数值仿真计算模拟真实条件，可以克服实验研究的不便，探究流场的动态过程，并在数值模拟和实流实验之间建立更紧密的互证关系，为气液两相流的测量提供更深入的借鉴依据和有力支撑．

笔者在50,mm 垂直上升管道内，利用Fluent 软件仿真，并通过实验研究了气液两相细泡流绕漩涡发生体流动发生气液两相涡街的一些现象．实验表明，截面含气率在小于10%时涡街是稳定的[4]，因此笔者分析了截面含气率在0～8%变化时对脉动升力以及漩涡脱落的影响．将计算流体动力学(computational fluid dynamics，CFD)仿真结果与实验比较，最大误差小于8%，平均误差小于4%．

1 建模与数值仿真

1.1 模型的选择与建立

考虑到在水平管段，气液两相流在运动过程中极易出现分层的现象，涡街流量计检测到的很多都是纯水的信息，失真太大；而在垂直上升管道内，气液两相流在重力和浮力等作用下，相对混合比较均匀，检测效果也很好，所以选择竖直管段为实验管段，直径D＝50,mm，仿真时建模也按该尺寸建立竖直管段．

从实际出发，涡街流量计需要有前后直管段来保证漩涡分离的稳定性，因此在建立仿真模型时，选取30D长的管道，前直管段处为181,mm，梯形柱漩涡发生体为19,mm，后直管段为400,mm．所选梯形柱漩涡发生体的尺寸为单相流产生稳定涡街的典型尺寸，即迎流面与管径比为0.28．由于二维数值仿真中省略了漩涡的拉伸弯扭项，忽略了边界层条件，造成了二维仿真结果与真实的三维流场存在较大差异，且漩涡自身还有三维的特性，因此，选择建立三维模型[5]．管内采用结构化网格六面体剖面，边界层与漩涡发生体梯形柱采用结构化网格四面体剖面，并进行光顺处理，如图1 所示．

图1 模型全景Fig.1 Model panorama

1.2 纯水仿真与可靠性分析

为检验模型的可靠性，根据纯水在管道中流动的情况分别进行数值仿真和实流实验．由于在单相流中涡街流量计的信号最强处为漩涡发生体后的1.5倍管径处[6-8]，因此选择该点检测出的仿真频率值与实验进行分析比对，如图2 所示．

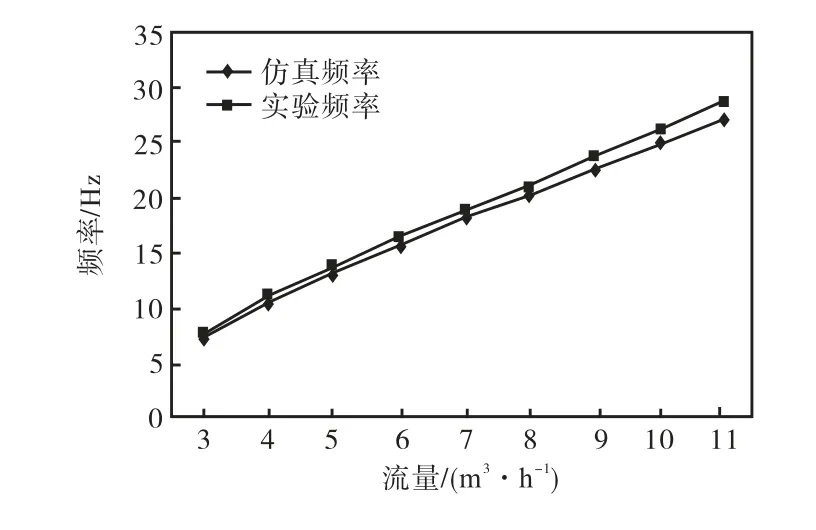
图2 纯水仿真结果与实验结果比对Fig.2 Comparison between simulation and experimental result in pure water

由图2 可见，仿真结果与实验结果相比，最大误差小于7%，平均误差小于5%，表明模型对流场的模拟结果可信．利用这个结果，再加入气相，可以进行气液两相流的数值仿真．

1.3 气液两相流的仿真

仿真条件如表1 所示．仿真时，在速度入口处先根据预定流量设定流速．开始只计算第1 相水相，待出口与入口的流量一致或差值足够小时，即收敛结果比较好时，添加第2 相气相继续计算[9]．共完成了5 组不同流量下(6,m3/h、7,m3/h、8,m3/h、9,m3/h和10,m3/h)不同截面含气率α(1%、2%、3%、4%、5%、6%、7%和8%)的数值仿真．与纯水仿真时一样，在漩涡发生体后1.5 倍管径处检测仿真频率，结果如图3 所示．

表1 仿真条件Tab.1 Simulation conditions

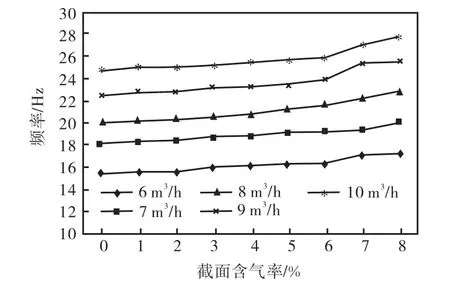
图3 不同截面含气率下仿真涡街信号频率变化Fig.3 Frequency change of simulation signal in different void fractions

由于固定水流量时，不同截面含气率下变化曲线变化趋势存在共性，因此仅分析水流量为6,m3/h 时不同截面含气率(0、2%、4%和6%)下的仿真脉动升力(图4)和仿真脉动升力功率谱密度(power spectral density，PSD)(图5)．

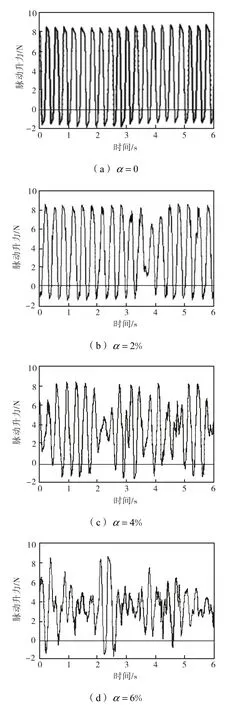
图4 水流量为6,m3/h时不同截面含气率下仿真脉动升力Fig.4 Simulation fluctuating lift in different void fractions when flow rate is 6,m3/h

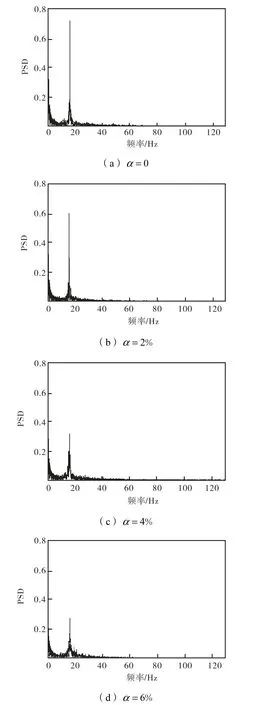
图5 水流量为6,m3/h 时不同截面含气率下仿真脉动升力功率谱密度Fig.5 Simulation power spectral density of fluctuating lift in Fig.5 different void fractions when the flow rate is 6,m3/h

可见，随着含气率上升，脉动升力的周期性被破坏得更为严重，随机性增强[10]，且脉动升力的幅值逐渐减小．脉动升力功率谱存在尖峰，表明有漩涡自梯形柱漩涡发生体交替脱落；尖峰峰值逐渐减小，而峰值对应频率逐渐升高，表现为随机振动中叠加了1 个周期性波动，这种周期性随截面含气率的增加而减弱.

2 实验系统及两相涡街的检测

2.1 实验系统

实验条件见表2，实验工质由已测定流量的水和空气分别送入混合器形成混合物后送入实验管段，其实验在天津大学电气与自动化工程学院油气水三相流综合实验装置上完成，实验装置如图6 所示．实验所用的涡街流量计为工业现场实用的压电式涡街流量计．内径D＝50,mm，涡街流量计安装在垂直上升测量管路上，其前后直管段分别为25D和30D．

表2 实验条件Tab.2 Experimental conditions

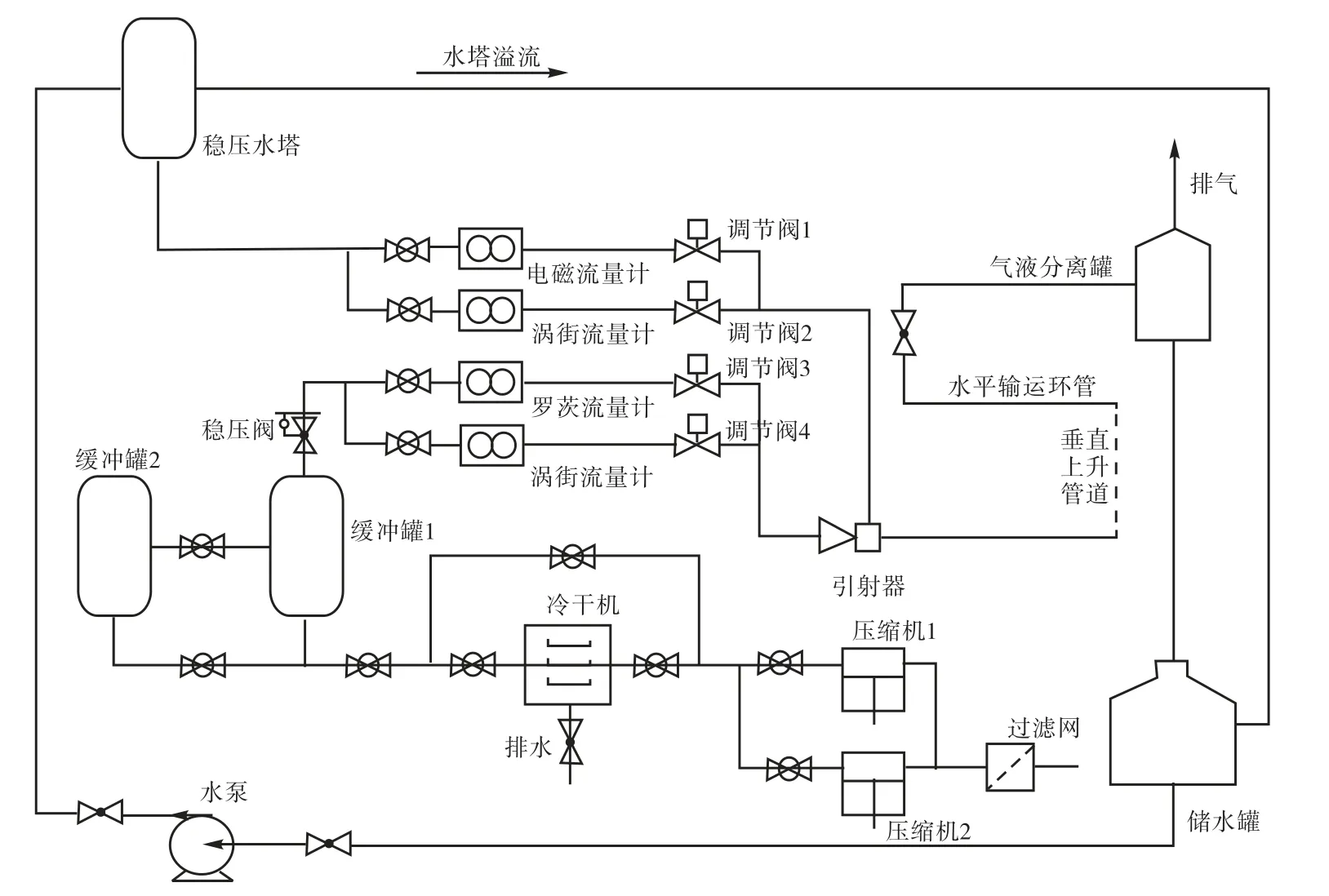
图6 多相流测量装置示意Fig.6 Sketch of multi-phase measuring devices

2.2 两相涡街的检测

实验中利用如图7 所示涡街信号采集系统，将涡街流量传感器探头输出的信号经电荷放大器、低通滤波器、NI-6009 数据采集卡，输入计算机存储．

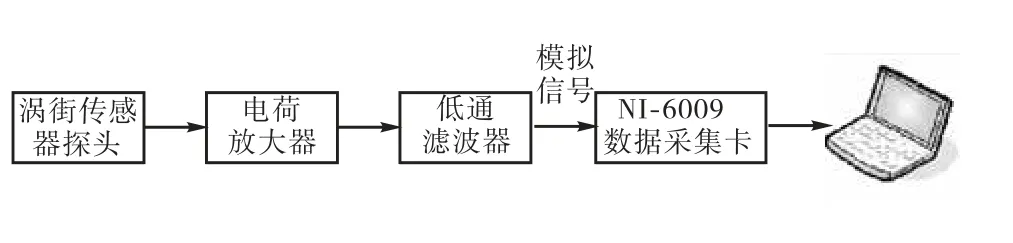
图7 涡街信号采集系统Fig.7 Vortex signal acquisition system

为了与数值仿真相比对，共完成了5 组不同流量下(6,m3/h、7,m3/h、8,m3/h、9,m3/h 和10,m3/h)不同截面含气率(1%、2%、3%、4%、5%、6%、7%和8%)的实流实验，实验频率如图8 所示．

图8 不同截面含气率下实验涡街信号频率变化Fig.8 Frequency change of experimental signal in different Fig.8 void fractions

实验分析方法与数值仿真相同，在水流量为6,m3/h 时对不同截面含气率(0、2%、4%和6%)下的脉动升力(图9)和脉动升力功率谱密度(图10)进行分析．

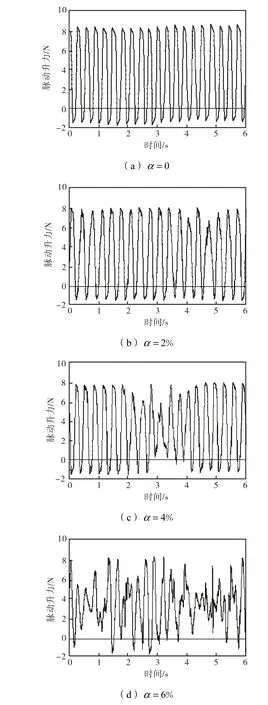
图9 水流量为6,m3/h时不同截面含气率下实验脉动升力Fig.9 Experimental fluctuating lift in different void fractions when flow rate is 6,m3/h

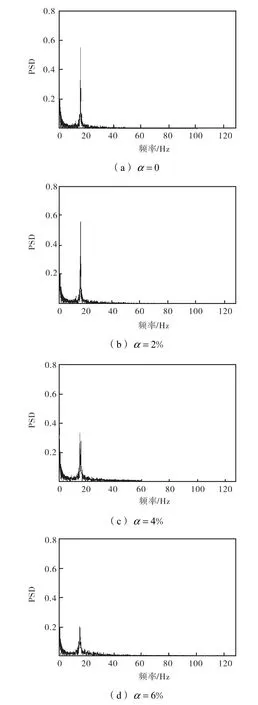
图10 水流量为6,m3/h时不同截面含气率下实验脉动升力功图10 率谱密度Fig.10 Experimental power spectral density of fluctuating lift in different void fractions when flow rate is 6,m3/h

可见，截面含气率的上升，严重破坏了脉动升力的周期性，增强了随机性，减小了振动幅值，脉动升力功率谱的尖峰表明尾流中存在稳定的涡街，尖峰峰值逐渐减小，峰值对应频率逐渐升高，同样表现为在随机振动中叠加了一个周期性随截面含气率增加而减弱的波动．

3 仿真与实验结果的对比与分析

将水流量为6 m3/h 的仿真数据与实流实验数据对比，如图11 所示，最大误差低于8%，平均误差低于4%，表明仿真结果非常贴近实际，在压力、速度等物理量上反映了真实流场的物理特性．

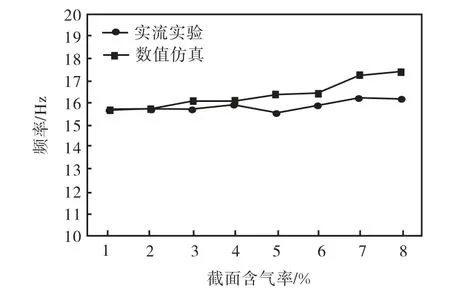
图11 水流量为6,m3/h的仿真数据与实流实验数据比较Fig.11 Comparison between simulation and experiment result when flow rate is 6,m3/h

单相流实验指出[4]，在一定雷诺数范围内，斯特劳哈尔数Sr是一个常量，流量qv与稳定的漩涡脱落频率f 的关系为

式中：d为漩涡发生体特征宽度；D为管径；m为发生体两侧弓形流通面积之和与测量管的横截面积之比．

实验中，单相流纯水 Sr = 0.16，为常数．与单相流纯水的数值相比，气液两相流同一流量下的Sr随截面含气率的变化而变化，说明气液两相流钝体绕流产生的漩涡中存在一定随机性，如图12 所示．

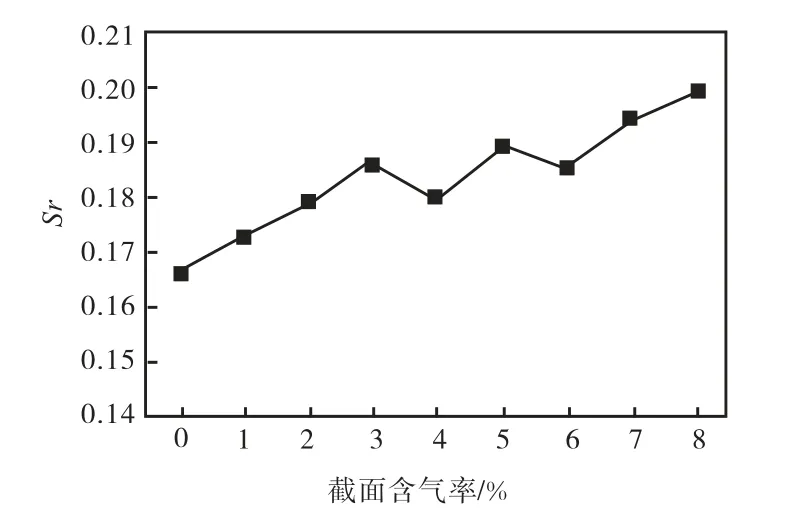
图12 气液两相流中截面含气率对斯特劳哈尔数的影响Fig.12 Impact of void fraction on Sr in gas-liquid two phase flow

在相同的截面含气率、不同水流量下Sr的变化情况如图13 所示．增多，振动的随机性增强，严重破坏了周期性．脱落的漩涡由于其中心吸入了气泡，使漩涡的能量比单相流中低，由此气液两相流中由漩涡脱落引起的脉动升力比单相流时小，且随含气率增加而减小．

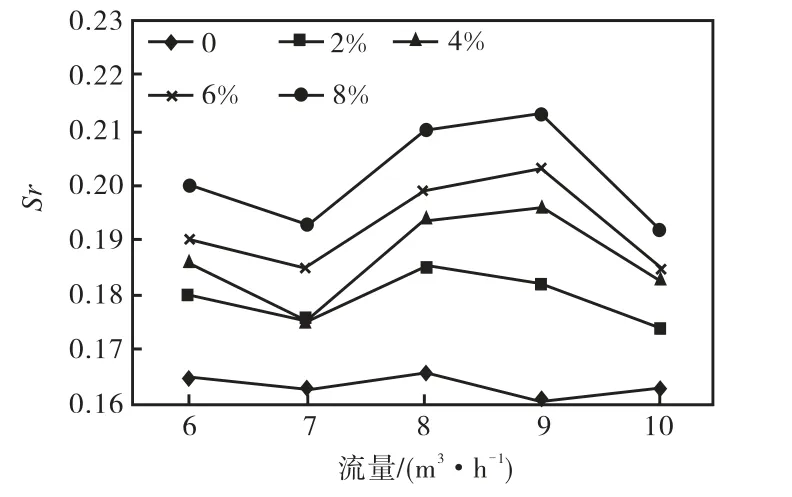
图13 相同截面含气率不同水流量下的斯特劳哈尔数变化情况Fig.13 Changes in Sr in the same void fraction under different water flows

可见，与纯水相比较，在相同截面含气率、不同水流量下，Sr波动更为明显，进一步说明了气液两相流钝体绕流产生的漩涡中存在一定随机性．

这种随机性是由气液两相细泡流中密度比水小很多的小气泡在压力梯度的作用下不断撞击梯形柱漩涡发生体引起的．随截面含气率的增加，气泡数量

与单相流纯水的数据相比，随着截面含气率的增加，升力功率谱的尖峰峰值减小，同样表明在柱体之前气泡的移动随机性增强；而峰值对应频率逐渐升高表明尾流中存在稳定的涡街，且漩涡脱落频率升高．脉动升力功率谱的尖峰表明尾流中存在稳定的涡街；尖峰峰值逐渐减小，峰值对应频率逐渐升高，表现为在随机振动中叠加了一个周期性的波动，这种周期性随截面含气率增加而减弱．

4 结 论

(1) CFD 仿真结果与实验对比，最大误差小于8%，平均误差小于4%．CFD 数值模拟可以真实地反映低含气率下实流流场中气液两相细泡流钝体绕流特性．

(2) 气液两相流中斯特劳哈尔数Sr在同一水流量下，随截面含气率的变化而变化，不再为常数；在相同截面含气率不同水流量下也不为常数．表现出气液两相流钝体绕流产生的漩涡存在一定的随机性．

(3) 在截面含气率低(小于10%，实验中小于8%)的情况下，随含气率的增加，气液两相流钝体绕流能产生稳定的涡街，引发的脉动升力幅值逐渐减小，振动随机性增强，破坏了周期性．

［1］Inoue A，Kozawa Y，Yokosawa M. Studies on two phase cross flow(Part I)：Characteristics around a cylinder [J].International Journal of Multiphase Flow，1986，12(2)：149-167.

［2］Hulin J P，Fierfort C，Condol R. Experimental study of vortex emission behind bluff obstacles in a gas liquid vertical two-phase flow[J].International Journal of Multiphase Flow，1982，8(5)：475-95.

［3］李永光，林宗虎，王树众. 气液两相流体涡街中漩涡结构的特性研究[J]. 西安交通大学学报，2006，30(2)：36-40.Li Yongguang，Lin Zonghu，Wang Shuzhong. Study of vortex street structure in a gas-liquid two-phase cross flow[J].Journal of Xi'an Jiaotong University，2006，30(2)：36-40(in Chinese).

［4］Shakouchi T，Tian D，Ida T. Measurement of flow rates of gas-liquid two-phase flow by Karman vortex[C]//Proceedings of the3rd International Symposium on Measurement Techniques for Multiphase Flows. Fukui，Japan，2001：83-89.

［5］周云龙，洪文鹏，王光培，等. 垂直上升通道内气液两相绕圆柱流动旋涡脱落频率和脉动升力的数值模拟[J]. 水动力学研究与进展，2007，22(2)：194-201.Zhou Yunlong，Hong Wenpeng，Wang Guangpei，et al. Numerical simulation of vortex shedding frequency and the oscillation lift based on gas-liquid two-phase flow around circular cylinders in the vertical pipeline[J].Journal of Hydrodynamics，2007，22(2)：194-201(in Chinese).

［6］姜仲霞. 涡街流量计[M]. 北京：中国石化出版社，2006.Jiang Zhongxia.Vortex Flowmeter[M]. Beijing：China Petrochemical Press，2006(in Chinese).

［7］Yokosawa M，Kozawa Y，Inoue A. Studies on two phase cross flow (Part II)：Transition Reynolds number and drag coefficient[J].International Journal of Multiphase Flow，1986，12(2)：169-184．

［8］Yokosawa M，Kozawa Y，Inoue A. Studies on two phase cross flow (Part Ⅲ)：Characteristics of unsteady flow behavior[J].International Journal of Multiphase Flow，1986，12(2)：185-202.

［9］陈 晨. 流场中气液两相流的三维仿真与实验研究[D]. 天津： 天津大学电气与自动化工程学院，2009．Chen Chen. Numerical and Experimental Research on Gas-Liquid Two-Phase Flow in Flow-Field[D].Tianjin：School of Electrical Engineering and Automation，Tianjin University，2009(in Chinese).

［10］孙志强，周洪亮. 管内气液两相流涡街稳定性分析[J]. 中南大学学报，2008，39(6)：1165-1169.Sun Zhiqiang，Zhou Hongliang. Analysis of stability of gas-liquid two-phase vortex street in conduits[J].Journal of Central South University，2008，39(6)：1165-1169(in Chinese).