一类四阶具阻尼非线性波动方程的初边值问题

高慧敏, 陈翔英

(1.连云港职业技术学院 江苏 连云港 222006;2.郑州电力高等专科学校 河南 郑州 450004)

一类四阶具阻尼非线性波动方程的初边值问题

高慧敏1, 陈翔英2

(1.连云港职业技术学院 江苏 连云港 222006;2.郑州电力高等专科学校 河南 郑州 450004)

研究一类具阻尼非线性波动方程的初边值问题

局部古典解和整体古典解的存在性和唯一性,其中,α,β>0,γ<0均为常数,u(x,t)为未知函数,φ(s),f(s)和g(s)为给定的非线性函数,u0(x)和u1(x)是给定的初值函数.

非线性波动方程;初边值问题;整体解

0 引言

研究四阶具阻尼非线性波动方程的初边值问题

(1)

(2)

(3)

其中,α,β>0,γ<0均为常数,u(x,t)为未知函数,φ(s),f(s)和g(s)为给定的非线性函数,u0(x)和u1(x)是已知的初值函数,下标x和t分别表示对x和t求导数.

方程 (1) 包含描述诸多物理现象的数学模型,如描述弹性杆中纵向应变波传播的是非线性波动方程

(4)

其中，p=3或p=5.方程 (4) 称为Pochhammer-Chree方程,或简称PC方程[1]. 文[2]研究弹性杆中的非线性波时,提出了如下四阶非线性波动方程：

(5)

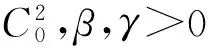
文[3-4]在研究非线性弹性杆的应变弧波时,给出如下非线性波动方程：

(6)

其中,b0,b2>0和b1≠0为常数,n为自然数.方程(5)和(6)的主要不同在于方程(5)比方程(6)多了流体力学阻尼项γuxxt.

文[5]研究了描述浅水波的方程:

utt-uxx-uxxtt=(u3)xx,

(7)

称为IMBq方程.文[6]研究在出现阻尼和外力的情况下,关于单原子链的晶格孤立子动力学时给出广义Boussinesq方程:

utt-uxx-uxxtt+βut+γuxxt=f(u)xx,

(8)

其中,常数β>0,γ<0,ut为Stokes阻尼，uxxt为流体动力学阻尼.

文[7]证明了非线性Pochhammer-Chree 方程 Cauchy问题解的存在性和解的爆破.文[8-9]分别证明了方程(5)和方程(6)广义形式的初边值问题整体古典解的存在性和唯一性,并给出了解爆破的充分条件.

关于方程(4)和方程(7)的广义形式,文[10]证明了整体古典解的存在性和唯一性,并给出了解爆破的充分条件.对于方程(8)还没有看到有文献讨论它的定解问题.作者将证明初边值问题(1)～(3)局部古典解和整体古典解的存在性和唯一性.

1 初边值问题(1)～(3)局部解的存在性与唯一性

为了将问题(1)～(3)化为等价的积分方程,引入Green函数.令K(x,ξ)是常微分方程边值问题

的Green函数,其中，α>0是实数,即

(9)

假设u0(x),u1(x)适当光滑并满足边界条件(2),u(x,t)是问题(1)～(3)的古典解,则方程(1)满足边界条件(2)的解u(x,t)满足积分方程

(10)

(10)式两边关于t在(0,t)上积分得

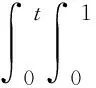
(11)

关于t再积分一次推出

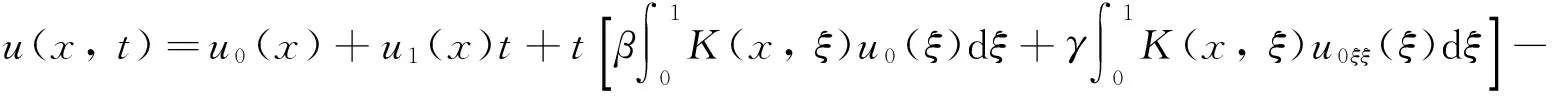
(12)

因此,问题(1)～(3)的古典解满足方程(12).由Green函数K(x,ξ)的性质,容易直接验证引理1成立.

引理1设u0,u1∈C2[0,1],u0(x)和u1(x)满足边值条件(2),φ∈C1(R),f∈C2(R)和g∈C(R)，如果u∈C([0,T]；C2[0,1])是积分方程(12)的解,则u(x,t)必是初边值问题(1)～(3)的古典解.

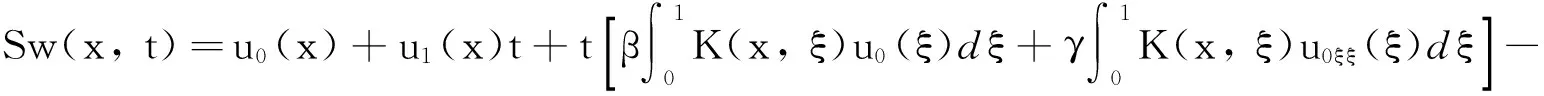
(13)

易知S把X(T)映射到X(T).

引理2假设u0,u1∈C2[0,1],u0(x)和u1(x)满足边值条件(2),φ∈C2(R),f∈C3(R),g∈C1(R),如果T相对于M是适当小,则S映P(M,T)到P(M,T)是严格压缩的.

证明(13)对ξ分部积分再对x求导,得

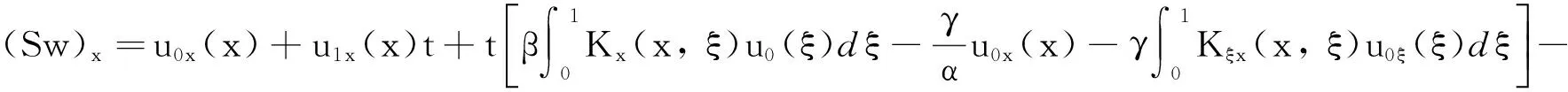
(14)

(14)对x求导,得

(15)

分别由

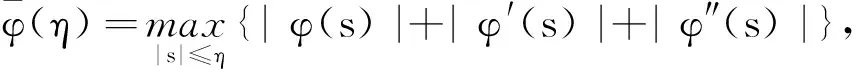
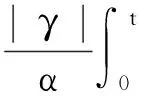
其中,Ci(i=1,2，…,9)是非负常数.如果T满足

(16)

则‖Sw‖X(T)≤2M.因此,如果(16)成立,则S映P(M,T)到P(M,T).

下面证明S:P(M,T)→P(M,T)是严格压缩的.设T>0,w1,w2∈P(M,T),由(13)可得

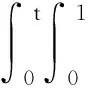
(17)

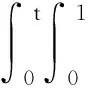
(18)

(19)

所以由(17)～(19)可见

(20)

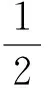
其中,C10,C11,C12是常数.如果T满足

(21)

定理1假设u0,u1∈C2[0,1],u0(x)和u1(x)满足边值条件(2),φ∈C2(R),f∈C3(R),g∈C1(R),则积分方程(12)有唯一解u∈C([0,T0);C2[0,1]),其中[0,T0)是解存在的最大时间区间,而且如果

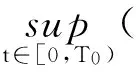
(22)

则T0=∞.

证明由引理2和压缩映射原理可知,对于适当选取的T>0,S有唯一不动点u(x,t)∈P(M,T),它显然是积分方程(12)的解.容易验证对于任意给定的T′>0,积分方程(12)至多有一个属于X(T′)的解.令[0,T0)为u(x,t)∈X(T0)存在的最大时间区间，利用文[11]中证明定理2.2的方法可证如果(22)成立,则T0=∞.定理证毕.

注1设u∈C([0,T0);C2[0,1])是积分方程(12)的解，即初边值问题(1)～(3)的解，则可推出u∈C2([0,T0);C2[0,1]).

2 初边值问题(1)～(3)的整体古典解

(23)

其中,A,B>0是常数,则初边值问题(1)～(3)存在唯一的整体古典解.

注2在定理证明中，‖·‖表示空间L2(0,1)中的范数和Mi(T)(i=1,2，…，6)是依赖T的常数.

证明(1)两边同乘以(2ut+2uut),在(0,1)上积分,并对x分部积分,可得

(24)

由于f′(s)在R上有界,有

两边关于t积分有

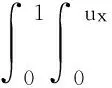
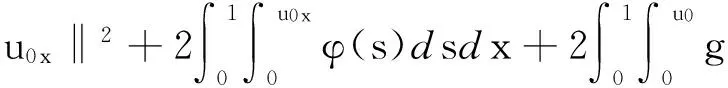
高良乡苗族有多少个芦笙调，采访了许多人，答案都不一样。杨家葬礼上组织者杨树彬十分肯定地说有360调，其中葬礼用的有160多调，其余都叫杂调（用于踩花山等活动）。

利用Poincar′e不等式

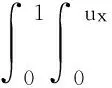
由于

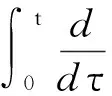
则

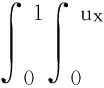
利用条件(23)得

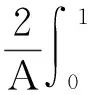
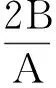
由Gronwall不等式推出

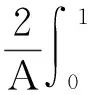
(25)

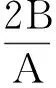
(26)

(12)对ξ分部积分可得

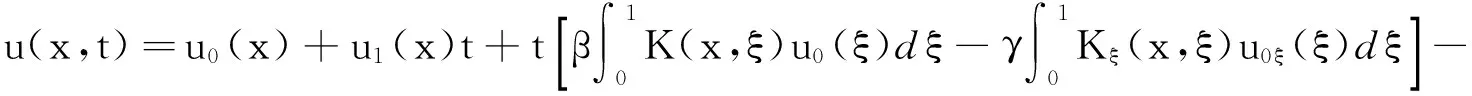
(27)

由(27)得

(28)

(29)

(29)两边同乘以uxt,得

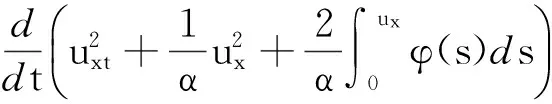
(30)

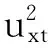
(31)

由Gronwall不等式导出

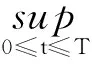
(32)

(28)对x求导两次，经估计可得

由Gronwall不等式

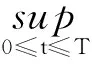
(33)

类似地有

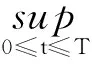
(34)

根据定理1和引理1知问题(1)～(3)有唯一整体古典解u(x,t).定理证毕.

致谢此文在郑州大学陈国旺教授的指导下完成，特此感谢！

[1] Clarkson P A,Levegue R J,Saxton R. Solitary-wave interactions in elastic rods[J].Stud Appl Math,1986,75(2):95-122.

[2] 朱位秋.弹性杆中的非线性波[J]. 固体力学学报,1980(2):247-253.

[3] Zhang Wei,Yang Guitong. Propagation of solitary waves in the nonlinear rods[J]. Appl Math Mech,1986,7(7):571-581.

[4] 张善元,庄蔚.非线性弹性杆中的应变弧波[J]. 力学学报,1988,20(1):58-66.

[5] Makhankov V G. Dynamics of classical solitons in nonintegrable systems[J].Physics Reports:Section C of Physics Letters,1978,35(1):1-128.

[6] Arévalo E,Gaididei Y,Mertens F G. Soliton dynamics in damped and forced Boussinesq equations[J]. Eur Phys J B,2002,27(1):63-74.

[7] Liu Yue. Existence and blow up of solutions of a nonlinear Pochhammer-Chree equation[J]. Indiana Univ Math J,1996,45(3):797-816.

[8] Chen Xiangying. Existence and nonexistence of global solutions for nonlinear evolution equation of fourth order[J].Appl Math,2001,16(3):251-258.

[9] Chen Guowang,Wang Shubin. Existence and nonexistence of global solutions for nonlinear hyperbolic equations of higher order[J]. Comment Math Univ Carolin,1995,36(3):475-487.

[10] Chen Guowang,Wang Shubin. Existence and nonexistence of global solutions for the generalized IMBq equation[J].Nonlinear Analysis:TMA,1999,36(8):961-980.

[11] 陈国旺，吕胜关. 人口问题中广义三维Ginzburg-Landau模型方程的初边值问题[J]. 应用数学学报，2000,23(4):507-517.

InitialBoundaryValueProblemforaClassofDampedNonlinearWaveEquationsofFourthOrder

GAO Hui-min1, CHEN Xiang-ying2

(1.LianyungangTechnicalCollege,Lianyungang222006,China;2.ZhengzhouElectricPowerCollege,Zhengzhou450004,China)

The existence and the uniqueness of the local classical solution and the global classical solution for the following initial boundary value problem for a class of damped nonlinear wave equations of fourth order were studied:

whereα,β>0,γ<0 were constants,u(x,t) denoted an unknown function,φ(s),f(s) andg(s) were given nonlinear functions,u0(x) andu1(x) were given initial value functions.

nonlinear wave equation;initial boundary value problem;global solution

O 175.26;O 175.29

A

1671-6841(2011)04-0019-09

2011-02-12

国家自然科学基金资助项目,编号10971199；河南省教育厅自然科学基金资助项目，编号2009C110006.

高慧敏(1982-),女， 讲师，硕士， 主要从事偏微分方程研究,E-mail:xuyonggaomin@yahoo.com.cn;通讯作者： 陈翔英 (1968-)，女，副教授，硕士，主要从事偏微分方程研究，E-mail:chenxiangying@126.com.