高层建筑周围行人高度风环境的数值模拟研究

吴义章， 张幸涛， 李会知， 王存海， 聂桂莆， 程站起

(1.郑州大学 土木工程学院 河南 郑州 450001;2.郑州东方钢结构装饰有限公司 河南 郑州 450003； 3.河南神火煤电股份有限公司 河南 永城 476600)

高层建筑周围行人高度风环境的数值模拟研究

吴义章1， 张幸涛1， 李会知1， 王存海2， 聂桂莆3， 程站起1

(1.郑州大学 土木工程学院 河南 郑州 450001;2.郑州东方钢结构装饰有限公司 河南 郑州 450003； 3.河南神火煤电股份有限公司 河南 永城 476600)

通过数值模拟方法对某高层建筑周围的行人高度风速场进行了计算，结合当地气象台的气象风速统计资料，给出了该建筑周围舒适性风的概率直方图，对行人高度风环境的舒适性作出了评价，并对一些可能存在不舒适风问题的位置点提出了控制措施.

高层建筑； 风环境； 数值模拟

0 引言

国内外实践[1-8]已证明，建筑个体和布置方式会使风环境产生种种变化，高大建筑周围很可能会产生局部强风，影响到行人的舒适与安全.例如，1982年1月5日，在美国纽约曼哈顿世界贸易中心双塔附近的广场上，37岁的女士露丝·斯菲波盖尔在行走时，被局部强风吹倒而受伤[2].这些事故实例反映了解决风环境问题的重要性.

在大规模的城市建筑群中新建一座高层建筑后是否会恶化原有的风环境，这是一个十分复杂的问题，往往需要通过风洞模型试验或数值模拟方法进行针对性的研究和验证.通过数值模拟方法来研究高层建筑工程完工后其周围2 m高度风速的分布状况，从而评估建筑物周围行人活动场所是否会产生不利的风环境.

1 行人高度风环境数值模拟计算

数值模拟计算的目标是得出各个来流风向下高层建筑周围各点2 m高处的速度值V与远前方来风10 m高处的速度值V10的比值V/V10，为利用当地的气象风速统计资料和风环境判据分析推断高层建筑周围行人高度风环境的舒适性提供数据基础.

1.1计算模型及计算区域网格的划分

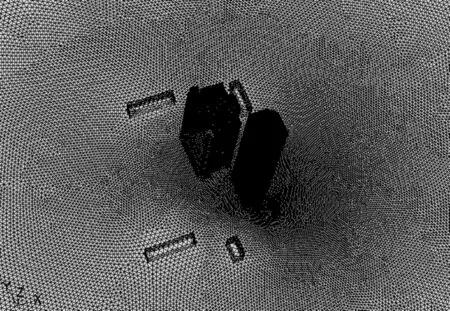
图1 建筑物表面网格划分的三维示意图Fig.1 Sketch map of building and grid

计算的高层建筑工程由一栋132 m高的办公大楼和一栋96 m高的住宅楼组成.从空气动力学理论来说，应该考虑邻近建筑物的影响，邻近建筑物高度均在19 m以下，因此，在进行数值模拟计算时主要从直观判断只考虑了周围可能带来影响较大的其他建筑物，而且从空气动力学的观点出发忽略了周围建筑物的局部细节，这是为了兼顾网格划分和计算容量的要求.

计算区域是长2 000 m、宽1 000 m、高600 m的长方体，在对计算区域进行网格划分时采用了非结构、混合网格划法，靠近建筑物表面附近采用了加密的网格形式，网格尺寸由内向外逐渐增大，网格划分后总计产生了97万多个体网格.图1是建筑物表面网格划分的整体三维视图.

1.2边界条件

数值模拟计算要求给出来流的边界条件，对于湍流来说，包括平均风速、湍动能k、湍能耗散率的剖面数据ε.

入口面的风速剖面是幂指数形式，采用C类地貌数据：

(1)

式中，V(z)为离地高度z处的平均风速,Vg为参考高度zg处的平均风速，计算中取为10 m高处的平均风速，在Fluent计算中取u=V(z),v=0,w=0.

入口面的湍动能和湍能耗散率按Paterson给出的公式计算：

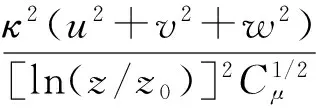
(2)

式中，κ=0.435为Kolmogoroff常数；z0为壁面的粗糙值，对于地面取0.024 m；Cμ是常数，取为0.09.

入口的平均风速剖面、湍动能和湍能耗散率均采用用户自定义函数(UDF)编程，通过Fluent的User-Defined-Functions接口对接实现入口风速的边界条件.

出口边界条件采用完全发展的出流情况(outflow).建筑物表面均采用无滑移边界条件(wall).计算域底面采用无滑移边界条件(wall)，以模拟实际地面；计算域顶面和两侧面采用自由滑移边界条件(symmetry)，以近似模拟开阔空间面.

1.3求解方法及收敛控制

为保证计算过程的数值稳定性和精度，离散化处理方程时采用二阶迎风格式.考虑固体壁面对流场的影响，采用非平衡壁面函数(non-equilibrium wall functions)以模拟近壁面附近复杂的流动现象.采用SIMPLEC算法求解有限体积积分得到的压力-速度相关控制方程组.采用分离式求解器和比较适于分离流的Realizablek-ε湍流模型进行计算.计算中监测相应模型的控制方程迭代残差以及所研究对象的一个迎风表面的风压系数变化，当控制量x-velocity、y-velocity、z-velocity continuity、ε、k的计算残差均小于0.000 1，且同时监测得到的一个迎风表面风压系数基本不发生变化、而且在合理的范围内时，认为所得流场进入了稳态，终止迭代计算.

1.4计算方案

在自然界中，高层建筑的来风风速Vs是一个变量，建筑周围2 m高处风速V是随Vs变化而变化的量，在计算中应考虑来风风速数值变化的影响.但在数值模拟计算中不能像数学函数计算那样把来流风速值设为变量一次完成计算，只能在不同的风速数值条件下进行多次重复计算，如果这样将大大增加工作量.从空气动力学理论来看，所计算的高层建筑物属于带锐缘尖角的钝体结构，所计算的风速范围属于高超临界雷诺数范围，因此，建筑周围风速分布应该满足相似理论，无量纲的风速比值应该不随来风风速的大小而变化，这一点通过只有办公大楼单体建筑存在时的计算获得了验证.验证时的风速条件按照式(1)、(2)给出，入口10 m高处的风速数值分别为10 m/s和20 m/s.在这个前提下，在计算中作为边界条件的来风风速不用根据建筑场地的风速统计数值资料而变化，这给数值模拟计算带来了很大方便，只需编写一个UDF函数表示的边界条件即可.各个风向下利用相同的风速条件进行数值计算，得出对应风向下的无量纲的风速比值，然后再来考虑实际建筑场地的风速条件，利用计算所得的风速比值结合当地的风速统计数据来分析实际建筑周围行人高度的风环境的舒适性.

不同来风风向下高层建筑周围行人高度的风速分布是不相同的，因此，计算模拟了16个来风风向(间隔22.5°)，分别为N(北风)、NNE(北东北风)、NE(东北风)、ENE(东东北风)、E(东风)、ESE(东东南风)、SE(东南风)、SSE(南东南风)、S(南风)、SSW(南西南风)、SW(西南风)、WSW(西西南风)、W(西风)、WNW(西西北风)、NW(西北风)、NNW(北西北风).

基于上述分析，计算中利用入口10 m高处中心点作为参考点，计算时该点风速数值取为15 m/s.在16个来流风向下分别计算，获得相应风向下的流速场，从而也获得了高层建筑周围行人高度的风速数据.

1.5结果及分析

经过计算获得了16个来风风向下该建筑工程周围2 m高处的风速矢量图，16个来风风向对应16个风速分布图，这里只给出其中1个，图2是东北风时2 m高处的风速分布矢量图.

因为这里分析建筑物周围风环境的舒适性需要的数据是各风向下的速度比值V/V10(θi)，因此利用Fluent的场变量设置功能得出V/V10的等值线图，图3为南风时的V/V10等值线图.下一节利用这里得出的速度比值V/V10结合建筑场地实际的气象风速统计资料，讨论该建筑工程周围行人高度风环境的舒适性.

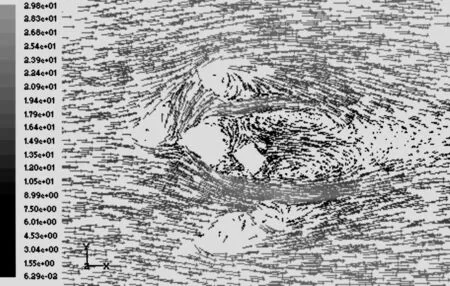
图2 东北风时建筑周围2 m高处的风速矢量图Fig.2 Distribution of horizontal vectors in 2 m-height plane

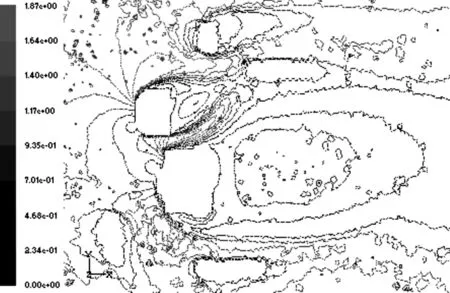
图3 南风时2 m高处的V/V10等值线图Fig.3 Isogram of V/V10 in 2 m-height plane

2 行人高度风环境舒适性的评估

建筑物周围的风环境，主要是指建筑物对自然界来风的影响和改变，局部是增大还是减小，变化程度是否可以接受，主要关注的是对行人活动造成的后果，从而引发建筑物周围行人高度风环境的“舒适度”概念.风的“舒适度”建立于人的感觉，因此因人而有所差异，不同学者的研究成果、表述方式也会有所不同.本文利用如下风环境判据：坐着的情况，风速V<5.7 m/s(界限风速)，站着的情况，风速V<9.3 m/s，行走的情况，风速V<13.6 m/s，当有80%的时间满足上述风速条件，这样就分别满足坐、站、行舒适性条件.

通过数值模拟计算已得出各风向下的速度比值V/V10，在这个前提下，如果知道高层建筑远前方来流风速V10，就可以知道高层建筑周围2 m高度风速V，进而利用风环境判据评估预测高层建筑周围行人高度风环境的舒适性.然而，计算机不能给出高层建筑远前方来流风速V10，这个V10必须从当地的气象台(站)的风速统计资料得出.

为了利用上述风环境判据判断某位置点是否满足舒适性要求，下面分三步进行分析处理和讨论：

(Ⅰ)根据数值模拟计算可以求出大楼建成后所有受关注的位置点，在16个风向下坐、站、行舒适性界限风速对应的气象台(站)10 m标高风速.由数值模拟计算得出V/V10，保持此风速比值不变，分别以风环境舒适性判据界限值V=5.7，9.3，13.6 m/s代入，即求出该风向下坐、站、行舒适性界限风速对应的气象台(站)风速.

以其中一点为例分析说明.图4是从数值模拟计算得出的位置1在大楼建成后V/V10比值随风向的变化，图5是大楼建成后位置1的舒适性界限风速对应的气象台(站)风速随风向变化.由图4可知，北风(N)时V/V10(5.7,N)= 0.46，由V=5.7 m/s得大楼前方来风10 m标高风速V10(5.7,N) =5.7/0.46=12.39 m/s，数值模拟计算采用的是大楼处于C类地貌，气象台(站)所处的位置是B类地貌，这样气象台(站)10 m标高风速是大楼前方来风10 m标高风速的1.27倍，进一步可以得出气象台(站)10 m标高风速V10j(5.7,N)= 12.39×1.27= 15.74 m/s；由V= 9.3 m/s得气象台(站)10 m标高风速V10j(9.3,N)=9.3/0.46×1.27= 25.68 m/s；图5中其他数据同理得出.

从图5中可以得出，北风(N)和东风(E)情况下，位置1坐着的舒适性界限风速(5.7 m/s)对应的气象台(站)10 m标高风速分别为15.74 m/s和6.83 m/s，也就是说，如果气象观测站测到的10 m标高北风风速为15.74 m/s或东风风速为6.83 m/s，那么，在位置1就会出现5.7 m/s的风速，如果位置1出现超过5.7 m/s的风速的概率超过20%，那么该处就不满足坐着的舒适性要求.但是，在当地是否出现东风或北风以及东风风速是否超过6.83 m/s或北风风速是否超过15.74 m/s或其他值以及这些风速值出现的概率，数值模拟计算不能给出.数值模拟计算只能在给定来风风速条件下得出高层建筑周围的风速分布数据，至于建筑的来风风速条件是什么状况，并不是决定于计算所给的条件，而是取决于当地的风气候，必须把当地的长周期气象风速资料与数值模拟计算获得的结果结合起来，才能分析推断建筑周围的实际风速分布及其舒适性状况.

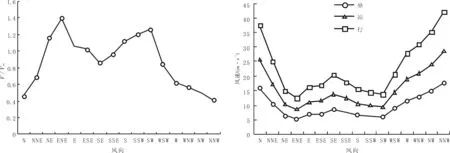
图4位置1的V/V10比值随风向的变化图5与位置1舒适性界限风速对应的气象站风速

Fig.4Ratio ofV/V10at site 1 with wind incidenceFig.5Wind velocity of weather station corresponding to the comfortable wind boundary

(Ⅱ)气象台站每隔3 h观测的风速和风向的记录是大量的离散数据，在应用时处理成概率分布数据，自然界梯度风风速超过某一数值发生的概率可用威布尔(Weibull)公式来描述.在给定风向上风速超过某一规定值V的发生概率P，用威布尔分布函数表示为

Pθ(V)=Aθexp[-(V/Cθ)Kθ],

(3)

式中，θ为扇形风向区，取16个风向区时，为22.5°的扇形区域，Pθ(V)为风向θ内、气象台10 m标高处风速超过V的概率，Aθ为风吹过θ内的时间比率，Cθ和Kθ为常数项.

通过对建筑地区的气象台风速资料所作的概率统计分析，可得出Aθ，Cθ和Kθ.例如，经分析，北风超过某一风速的概率表达式为

P1(V)=0.263 exp[-(V/4.76)1.7].

(4)

根据式(4)可以得到每年北风风速超过任意给定风速值的概率.因为风往往具有季节性，可以对各个季节的数据分别分析，给出各季节(如夏季和冬季)在某一风向下超过某一风速值的概率，以便按季节分析风环境的舒适性，为设计者提供更合理的风环境舒适性数据.

(Ⅲ)分析坐着的情况其舒适性界限风速发生的概率计算方法.由第(Ⅰ)步查图5知刮北风时如在位置1坐着休息的舒适性界线风速5.7 m/s对应的气象台风速为15.74 m/s，即气象台测出的北风风速超过15.74 m/s时，位置1的风速超过5.7 m/s.其发生概率也即时间频率由式(4)计算为

P1(V)=0.263 exp[-(15.74/4.76)1.7]=1.27×10-4.

(5)

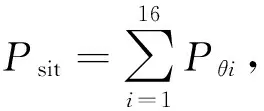
研究发现，如果是对全年的风速数据进行分析，得出的各位置点均满足坐、站、行舒适性条件，这是因为风的季节性比较强，在一个季节中，往往是某一风向起主导作用，另一个季节中，往往是另一风向起主导作用，而一个位置点往往是在某一个或几个来风风向上才出现风速增大的情况，这样一来就出现这种情况，某一位置在其中一个季节不满足舒适性条件，但在其他三个季节满足舒适性条件，全年总平均仍满足舒适性条件.

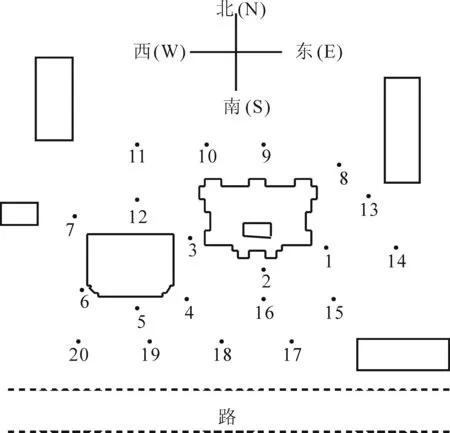
图6 建筑周围受关注点位置示意图Fig.6 Sketch map of sites concerned around the building

图6是建筑周围受关注点位置示意图，图7、图8分别是分季节计算(夏季和冬季)的坐、站、行的舒适性概率直方图.由图7可以看出，在夏季，位置3、6、14不满足坐着的舒适性条件，但其中位置3是两楼之间的夹道，位置6是楼拐角，此两位置均不是休憩场所，估计不会有人在此坐着休息，不满足坐着休息的舒适性条件也没关系，位置14是空地，若设为休憩场所，则不能取得满意的效果；由图8可以看出，在冬季，位置3、15、16不满足坐着的舒适性条件，其中位置15、16是空地，若设为休憩场所，则不能取得满意的效果，应给予关注.由图7、8可以看出，在夏、冬两季，除位置3外各位置均满足站立和行走的舒适性条件.在冬季强风时，位置3、7是风速增大区，从安全角度考虑，可设置盆景、围栏等，控制或减少人从此绕走；在夏季强风时，位置3、6是风速增大区，应给予关注，对于位置3，建议采用一定的封闭措施.

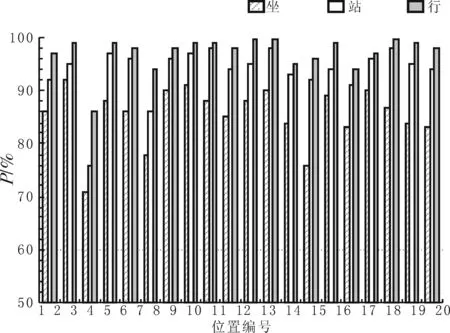
图7 夏季舒适性风的概率直方图Fig.7 Probability diagram of comfortable wind in summer

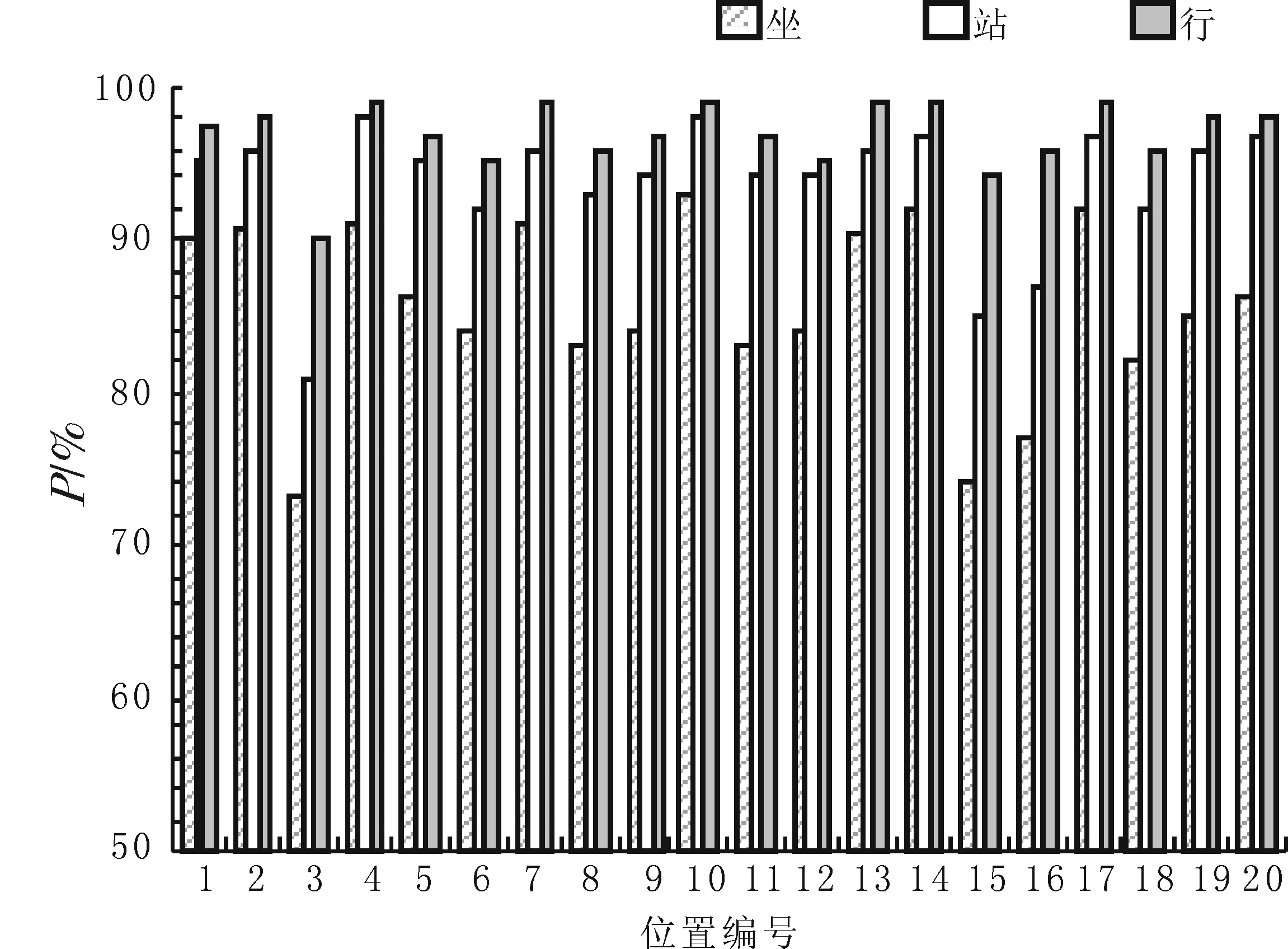
图8 冬季舒适性风的概率直方图Fig.8 Probability diagram of comfortable wind in winter

3 结论

高层建筑周围很可能会产生局部强风，影响到行人的舒适与安全.为了评估两个相邻的高层建筑周围的行人高度风环境的舒适性与安全性，通过数值模拟方法对该高层建筑周围的行人高度风速场进行了计算，结合当地气象台的气象风速统计资料，给出了该建筑周围舒适性风的概率直方图，对行人高度风环境的舒适性作出了评价，并对一些可能存在安全问题的位置点提出了控制措施.

研究表明，由于风的季节性比较强，某一(些)位置在其中一个季节不满足舒适性条件，但在其他三个季节满足舒适性条件，如果按一年作为评估周期对行人高度风环境的舒适性进行评估，往往得出满足舒适性条件的结论，这是一种笼统而不科学的处理方法，应按季节作出风环境舒适性评估，也可以按月份作出风环境舒适性评估.

[1] 埃米尔·希缪，罗伯特·斯坎伦.风对结构的作用:风工程导论[M].刘尚培，项海帆，谢霁明，译. 上海：同济大学出版社，1992:155-166.

[2] 关滨蓉，马国馨.建筑设计和风环境[J].建筑学报，1995,17(11)：44-48.

[3] 姜瑜君，桑建国，张伯寅. 高层建筑的风环境评估[J].北京大学学报：自然科学版，2006，42(1)：68-73.

[4] 陈建国，钱炜祺，符松. 蓝旗营住宅楼群风环境数值模拟[J].清华大学学报：自然科学版，2003，43(8)：1074-1078.

[5] 张爱社，张陵，周进雄.两个相邻建筑物周围风环境的数值模拟[J].计算力学学报，2003，20(5)：553-558.

[6] Murakami S,Deguchi K. New criteria for wind effects on pedestrians[J].Journal of Wind Engineering and Industrial Aerodynamics,1981,7(3): 289-309.

[7] Bottema M. A method for optimization of wind discomfort criteria[J].Building Environment,2000,35(1):1-18.

[8] Ferreira A D,Sousa A C,Viegas D X. Prediction of building interference effects on pedestrian level comfort[J].Journal of Wind Engineering and Industrial Aerodynamics,2002,90(4):305-319.

NumericalSimulationofthePedestrianLevelWindEnvironmentAroundHigh-riseBuildings

WU Yi-zhang1, ZHANG Xing-tao1, LI Hui-zhi1, WANG Cun-hai2, NIE Gui-pu3, CHENG Zhan-qi1

(1.CollegeofCivilEngineering,ZhengzhouUniversity,Zhengzhou450001,China;2.ZhengzhouEasternSteelStructure&DecoratingCo.Ltd,Zhengzhou450003,China;3.HenanShenhuoCoalIndustry&ElectricPowerCo.Ltd,Yongcheng476600,China)

The pedestrian level wind environment around high-rise buildings was studied by numerical simulation. The probability of comfortable wind was obtained by combining weather station wind data with the data from numerical simulation. The comfortable state of pedestrian level wind was predicted. The measure to improving wind environment of some areas was presented.

high-rise building;wind environment;numerical simulation

TU 119.4

A

1671-6841(2011)04-0110-06

2010-12-24

国家自然科学基金资助项目，编号10802078.

吴义章(1970-)，男，高级工程师，硕士，主要从事结构工程研究，E-mail:wyz@zzu.edu.cn.