孔洞石墨烯纳米带的电子输运性质

孙大立 彭盛霖 欧阳俊 欧阳方平,2,*

(1中南大学物理科学与技术学院,长沙410083;2北京大学化学与分子工程学院,北京分子科学国家实验室,北京100871)

孔洞石墨烯纳米带的电子输运性质

孙大立1彭盛霖1欧阳俊1欧阳方平1,2,*

(1中南大学物理科学与技术学院,长沙410083;2北京大学化学与分子工程学院,北京分子科学国家实验室,北京100871)

基于密度泛函理论的计算模拟,对含有孔洞的zigzag型石墨烯纳米带(N=17,N为碳链数目)结构进行优化,进一步计算得到体系存在不同孔洞时的电子输运性质.研究结果表明:当存在单个孔洞时,体系的导电性不仅与量子限域效应有关,还受到孔洞对称性的束缚,且斜向对称比纵向对称受到的束缚更大;对于双孔洞的情况,由于孔洞间的耦合作用,体系的导电性在较大距离范围内大体上随孔洞间距的增大而增强,同时会出现一些量子现象,这可用一维对称双势垒模型来解释.

石墨烯纳米带;纳米孔洞;量子限域效应;对称性

1 引言

石墨烯纳米带因具有独特的几何结构、丰富的电子学性质而有广泛的应用前景.在制备石墨烯纳米带中不可避免地存在缺陷,比如杂质原子取代、1-2空位缺陷3-6等等,缺陷的存在会对纳米带的电学、7磁学8等性质造成影响,从而给石墨烯纳米带的应用带来了很多的未知因素.

孔洞结构是在制作石墨烯纳米带过程中不可避免产生的缺陷,研究此种缺陷对体系物性的影响9以及碳基纳米器件10的制作都有着重要的指导意义.

Rosales等11研究了超晶格结构的孔洞模型,比较了不同周期、不同形状以及有无纵向对称性对电导的影响.发现孔洞边缘与纳米带边缘的距离跟电导值成负相关,关于纵向对称菱形的电导大于非对称菱形的;随着孔洞间距的增大,在电导谱的中部能量处有更多的带隙与导带形成,同时中央带隙的宽度减小.Topsakal等12在超晶格结构的孔洞模型基础上,从另一个方向出发,研究了相同孔洞在不同位置时模型带隙的变化,发现其大小随孔洞的移动而发生上下波动,证明缺陷的位置对石墨烯纳米带的电学性质有着较大影响.Zheng等13研究的模型是在散射区内仅存在一个孔洞,引入自旋后计算其对输运性质的影响,发现矩形和正三角形孔洞的存在使得石墨烯纳米带的导电性有所下降,根据量子限域效应,矩形空洞模型的导电性弱于正三角形孔洞模型的导电性;由于正三角形孔洞的非对称性,体系自旋无法抵消,在缺陷处产生附加能量,导致体系的状态密度(DOS)曲线图中的间隙不再关于零点对称.

本文通过对多种类型单孔洞模型的计算,研究了影响体系输运性质的主要因素;并由此出发,通过比较不同距离的双孔洞对体系造成的电学性质的影响来研究孔洞之间的相互作用.

2 计算模型和方法

2.1 模型的选取和建构

图1 含正六边形孔洞的石墨烯纳米带(ZGNR)模型Fig.1 Zigzag graphene nanoribbon(ZGNR)model with a hexagon holedashed area for semi-infinite long electrode and the intermediate area for scattering region;S:source electrode;D:drain electrode

采用N=17(N为碳链数目)的zigzag型石墨烯纳米带(ZGNR)进行计算研究.如图1所示,阴影部分表示电极,其结构实际上是半无限长的石墨烯纳米带,S代表源电极,D代表漏电极;中间区域为散射区.在散射区石墨烯中去掉22个碳原子构建一个孔洞,整个输运体系约含672个原子.孔洞的尺寸较大,这样对系统的输运性质就会有较大的影响,便于研究.为了使模型结构更加稳定,采用吸附氢的方法将边缘碳原子的悬挂键进行饱和,避免悬挂键.构建了多种孔洞模型以便系统地分析孔洞的存在对石墨烯纳米带的输运性质带来的影响.

2.2 计算方法和参数

对含有孔洞的ZGNR模型,均采用基于密度泛函理论的广义梯度近似(GGA)方法14进行优化,进一步计算可得到体系存在不同孔洞时的电子输运性质.

计算中平面波的截止能量取为2040.85 eV,布里渊区采样点集采用1×1×500,将能量变化小于10-6eV时定为收敛标准.基于以上参数,我们对模型的导电性进行了计算,并且同完整ZGNR的导电性质作了比较.所有的计算均采用ATK(Atomistix ToolKit)程序包完成.

3 计算结果与讨论

3.1 单孔洞石墨烯纳米带的电学性质

研究了孔洞方向性以及形状对单孔洞ZGNR的电子输运性质的影响,并在此基础上讨论了孔洞对称性的作用.

3.1.1 孔洞的方向性对电子输运性质的影响

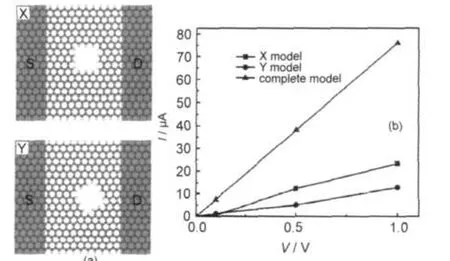
图2 关于轴向对称的矩形孔洞(X)及非轴向对称的矩形孔洞(Y)模型(a)及其I-V曲线图(b)Fig.2 ZGNR models with a rotational symmetry rectangular hole(X)and a non-rotational symmetry rectangular hole(Y)(a),and their I-V curves(b)The I-V curve of complete ZGNR in(b)is for comparison.

图2为关于轴向对称的矩形孔洞(X)及非轴向对称的矩形孔洞(Y)模型(a)及其I-V曲线图(b).如图2(a)X、Y模型所示,在中心散射区内有两种矩形孔洞,它们的大小、形状完全相同,只是方向有区别.图2(b)显示出了构建模型及完整ZGNR在0.1、0.5和1.0 V三处电流的大小.从图中可以看出,完整的ZGNR出现典型的导体性质.由于孔洞的存在,上述X、Y两种模型的I-V曲线都呈现出明显的半导体性质,且导电性明显降低.在电压较低时,X、Y两者的电流值都很小,在电压较大时,模型X的电流明显高于模型Y,这可用量子限域效应13来解释,即模型X的孔洞边缘到纳米带边界的距离大于模型Y,因此导电性较强.

3.1.2 面积相当、形状不同的孔洞对电子输运性质的影响

当石墨烯纳米带中存在较大的孔洞时,体系的输运性质与孔洞的形状有着紧密的联系,为了弄清楚这其中的关系,我们构建了三种面积相当但形状不同的孔洞,如图3(a)模型A、B、C所示.为了保证面积相当,三种模型去除的碳原子数基本相同,总原子数在670个左右.

如图3(b)所示,三种模型的I-V曲线都呈现出半导体性质,且导电性相对于完整的ZGNR而言大幅度下降.在电压较低时,电流值都很低,因此我们将研究重点放在较大电压的情况:当电压逐渐增大时,三者的电流差距逐渐增大,发现三角形孔洞模型的导电性最强,矩形次之,六边形的导电性最弱.

图3 面积相当形状不同三种孔洞模型(A,B,C)(a)及其I-V曲线图(b)Fig.3 Three ZGNR models with about the same area but different shapes(A,B,C)(a)and their I-V cuves(b)The I-V curve of complete ZGNR in(b)is for comparison.

比较模型A和B.对于模型A,三角形孔洞的顶点处由于氢饱和又形成了新的化学键,因此其输运性质与未去除顶点处碳原子的模型基本一致(经计算得知,前者的导电性略高于后者).同时很明显可以看出,模型A的孔洞边缘与纳米带边缘的距离总体上大于模型B,根据量子限域效应,A的导电性强于B,这与计算结果相吻合.

再来比较模型B和C.从模型图中可以看出,B中孔洞边缘与纳米带边缘的距离与C的基本一致,甚至还要小一些.若用量子限域效应来判断的话,B的导电性应该略小于C,这与计算结果中B的导电性明显大于C相矛盾.

3.1.3 孔洞的对称性对电子输运性质的影响

通过对前面几种模型的计算分析,我们发现量子限域效应在解释孔洞所引起的电学性质方面有很大的应用前景,许多现象都可以得到解释,但同时也发现了一些量子限域效应无法解释.因此我们就应该深入讨论其他的一些因素.

重新比较3.1.1节中X、Y两个模型,发现模型X是关于纵向对称的,而模型Y是关于斜向对称的;在3.1.2中,模型B是关于纵向对称的,而模型C不仅关于纵向对称,还关于斜向对称.两种对比的结果都是在较大电压下,关于纵向对称的模型的导电性强于关于斜向对称的模型.结合3.1.2节中的模型A可以得出以下规律:模型的导电性不仅受量子限域效应的影响,还受到对称性的束缚,15纵向对称受到的束缚较小,斜向对称受到的束缚较大.下面,我们通过进一步的计算对上述规律进行验证.

图4列出了四种不同类型孔洞的ZGNR模型,尽管它们的形状各不相同,但有着一个相同点,即孔洞上下边缘距离纳米带的边缘大小相同,这就最大程度地限制了量子限域效应对模型电学性质的影响.

由于在大电压领域,体系的量子效应影响相对较弱,因此为了验证假设的正确性,我们需要比较较大电压下四种模型的导电性质.

当电压为1.0 V时,D、E、F、G四种模型的电流分别为25.8967、23.3125、22.833、819.6344 μA,由此可以看出,电压为1.0 V时的四种模型的导电性按D、E、F、G的顺序依次减弱.比较模型E、F可知,孔洞的纵向宽度越大,导电性越小,但影响程度很小;模型D与F、E与G的差异也完全可用量子限域效应来解释.

图4 含有四种不同类型孔洞的ZGNR模型Fig.4 ZGNR models with four kinds of holes(D)trapezia,(E)rectangle with about the same length of sides, (F)rectangle with different lengths of sides,(G)rhombus

对于模型D、E的导电性差异,用量子限域效应已无法解释.从图4中可知,D的孔洞既不关于纵向对称,也不关于斜向对称,因此其导电性不受对称性的束缚;而E则受到纵向对称的束缚,导致其导电性降低.通过这一比较,我们还发现与量子限域效应这一因素相比,对称性束缚的影响程度更大一些.

对于模型F、G,尽管F的纵向宽度大于G,且受到纵向对称的束缚,但其电导性依然高于G,原因就在于模型G关于斜向对称,受到的束缚更强.

通过对以上计算结果的比较分析,我们验证了此规律的正确性,而这一规律对以后分析研究单孔洞模型的电学性质将有着重要的指导意义.

3.2 双孔洞石墨烯纳米带的电学性质

近年来,含有各类缺陷的石墨烯纳米带已经得到了较为广泛的研究,尽管对于存在双孔洞缺陷的情况,也有不少报道,16但发现有一个尚待解决的问题就是相互独立的孔洞之间的耦合效应是如何表现的.

如图5(a)所示,在完整ZGNR中构建两个六边形孔洞,通过调节d(用两孔洞间相隔六元环的个数来表示)的大小来研究双孔洞之间的相互作用.

将双孔洞看作是两个超级原子,17其距离较小时两超级原子的原子轨道发生重叠,导致局域态的产生,进而使体系的电学性质发生改变.因为随着距离的减小,耦合作用不断加强,局域能量增加,我们猜想体系的导电性应该随着孔洞距离d的增大而增强.

图5 六边形双孔洞模型(a)及电压分别为0.1和1.0 V时电流随距离d的变化(b)Fig.5 ZGNR models with double-hexagon hole(a)and the change of current along with distance(d)under 0.1 and 1.0 V(b)d represents the distance between the two holes,which is expressed by the number of the small hexagons between the holes.

如图5(b)所示,我们将0.1和1.0 V电压下电流随d的变化曲线画出.图中曲线的线形明显与猜想不同,除此之外两图之间也存在着显著的差别.左图显示,随着d的增大,电流的变化并非是单调的,而是波动变化,且总体上是上升的;右图显示,在距离d＞2的情况下,电流随着距离的增大而增大(类似情况见文献11),并在d=2处有一个极小值.

上述现象可用一维对称双势垒18的观点来解释.如果把石墨烯纳米带中的孔洞看作是一个势垒,那么本节所讨论的双空洞模型就转化成了一维对称双势垒模型,如图6所示(图中仅定性地给出了透射系数大小与距离d的关系).

在电压较小(如0.1 V)时,电子获得的能量小于势垒高度,体系的导电性质取决于透射系数的大小.从文献13中我们了解到,由两个势垒形成的阱具有分立的能级,当入射波的能量等于或接近某一个能级时,共振遂穿现象将发生,19此时的透射系数则比较大.随着距离d的不断变大,孔洞的耦合作用减小,电流值应该是不断增大的.但考虑到双势垒的分立能级也在不断地变化,当某一d下的能级与0.1 V下电子获得的能量接近时,此时的透射系数就会比较大,其导电性会高于两侧,于是就会出现波动变化.在电压较大(如1.0 V)时,电子获得的能量大于势垒高度,此时电流的大小基本上只受耦合这一个因素的影响,即随着距离的增大不断增大.在图5(b)中我们可以看出,当d＞2时,电流随着距离的增大而增大,验证了上述观点.但是,当d=2时,电流值显著地减小,这就需要用双势垒中的共振现象来解释了.如图6所示,电子的入射能量大于势垒高度时,在宏观状态下电子会完全通过势垒.但在微观状态下,电子的透射系数并不一定是1.根据量子力学的观点,由两个势垒形成的阱具有分立的能级,在电子的入射能量高于势垒时,当入射波的能量接近或等于某一个能级时,会发生共振现象,透射系数急剧下降.d= 2时双势垒所形成的阱的某一能级与1.0 V下电子的能量最接近,因此发生共振现象,导电性显著降低.

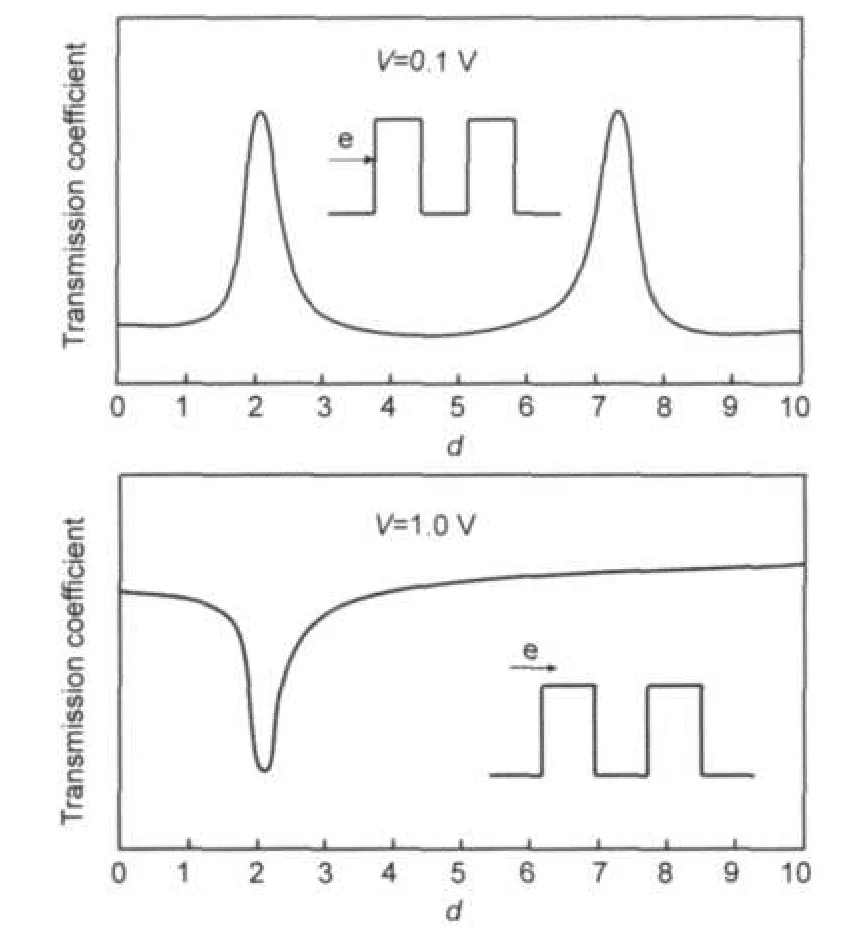
图6 两种情况下透射系数与距离d的关系简图Fig.6 Diagram for the connection between thetransmission coefficient and distance d

4 结论

利用基于密度泛函理论的广义梯度近似对含有孔洞的ZGNR(N=17)进行了计算分析.结果表明:孔洞的存在使得ZGNR的导电性大幅度减小,由导体变成了半导体;对于单孔洞的情况,模型的导电性不仅受到量子限域效应的影响,还受到对称性的束缚,且斜向对称比纵向对称受到的束缚更大;对于双孔洞的情况,由于孔洞间的耦合作用,体系的导电性在较大距离范围内大体上随孔洞距离的增大而增强,但会出现一些量子现象,这用一维对称双势垒模型可解释:在小电压下,体系电流呈现波动性变化,这与共振遂穿现象有关;在大电压下,体系电流有突然下降的现象,这与势阱出现共振有关.

(1) Peres,N.M.R.;Klironomo,F.D.;Tsai,S.W.;Santos,J.R.; Lopes,J.M.B.;Castro,A.H.Eur.Phys.Lett.2007,80,67007.

(2) Ouyang,F.P.;Yang,Z.X.;Xiao,J.;Wu,D.;Xu,H.J.Phys. Chem.C 2010,114,15578.

(3) Palacios,J.J.;Rossier,J.F.;Brey,L.Phys.Rev.B 2008,77, 195428.

(4) Ouyang,F.P.;Wang,H.Y.;Li,M.J.;Xiao,J.;Xu,H.Acta Phys.Sin.2008,57,7132.[欧阳方平,王焕友,李明君,肖 金,徐 慧.物理学报,2008,57,7132.]

(5) Ouyang,F.P.;Xu,H.;Lin,F.Acta Phys.Sin.2009,58,4132. [欧阳方平,徐 慧,林 峰.物理学报,2009,58,4132.]

(6) Ouyang,F.P.;Wang,X.J.;Zhang,H.;Xiao,J.;Chen,L.N.; Xu,H.Acta Phys.Sin.2009,58,5640. [欧阳方平,王晓军,张 华,肖 金,陈灵娜,徐 慧.物理学报,2009,58,5640.]

(7) Yan,J.Y.;Zhang,P.;Sun,B.;Zhou,L.;Wang,Z.G.;Duan,S. Q.;Zhao,X.G.Phys.Rev.B 2009,79,115403.

(8) Shen,T.;Wu,Y.Q.;Capano,M.A.;Rokhinson,L.P.;Engel,L. W.;Ye,P.D.Appl.Phys.Lett.2008,93,122102.

(9) Xiong,Y.J.;Kong,X.L.Physica B 2010,405,1690.

(10) Zhou,Y.X.;Ernzerhof,M.J.Chem.Phys.2010,132,104706.

(11) Rosales,L.;Pacheco,M.;Barticevic,Z.;León,A.;Latgé,A.; Orellana,P.A.Phys.Rev.B 2009,80,073402.

(12)Topsakal,M.;Aktürk,E.;Sevinçli,H.;Ciraci,S.Phys.Rev.B 2008,78,235435.

(13) Zheng,X.H.;Zhang,G.R.;Zeng,Z.;Víctor,M.;García,S.; Colin,J.L.Phys.Rev.B 2009,80,075413.

(14) Perdew,J.P.;Burke,K.;Ernzerhof,M.Phys.Rev.Lett.1996, 77,3865.

(15) Ren,Y.;Chen,K.Q.J.Appl.Phys.2010,107,044514.

(16)Bahamon,D.A.;Pereira,A.L.C.;Schulz,P.A.Phys.Rev.B 2010,82,165438.

(17) Canning,A.;Galli,G.;Kim,J.Phys.Rev.Lett.1997,78,4442.

(18)Yamamoto,H.Appl.Phys.A 1987,42,245.

(19) Zhao,X.P.;Wang,C.K.Journal of Shandong Normal University 1999,14,3. [赵锡平,王传奎.山东师大学报自然科学,1999,14,3.]

December 12,2010;Revised:January 15,2011;Published on Web:April 8,2011.

Electronic Transport Properties of Graphene Nanoribbons with Nanoholes

SUN Da-Li1PENG Sheng-Lin1OUYANG Jun OUYANG Fang-Ping1,2,*
(1School of Physics Science and Technology,Central South University,Changsha 410083,P.R.China;2College of Chemistry and
Molecular Engineering,Beijing National Laboratory for Molecular Sciences,Peking University,Beijing 100871,P.R.China)

Based on the density of the general theory,the structures of ziqzag graphene nanoribbons (ZGNRs)(N=17,N is the number of carbon chain)with nanoholes are optimized and then get the transport property of the electrons in these systems with different holes through the calculation.The results show that the conductance is not only related to the quantum confinement effect,but also confined by the symmetry of the hole and the configuration of the diagonal symmetry is larger than the longitudinal symmetry′s in the presence of a single-hole.In the case of two holes,the conduction of the system is advanced with the growth of the distance between the two holes because of the coupling effect.At the same time,we can get some quantum phenomenon which can be explained by the model of onedimensional double barrier.

Graphene nanoribbon;Nanoholes;Quantum confinement effect;Symmetry

O641

*Corresponding author.Email:ouyangyh@pku.edu.cn;Tel:+86-13811800095.

The project was supported by the China Postdoctoral Science Foundation(201003009,20090460145),Fundamental Research Funds for the Central Universities,China(201012200053),Science and Technology Program of Hunan Province,China(2010DFJ411),and Science Develop Foundation

of Central South University,China(08SDF02,09SDF09).

中国博士后科学基金特别资助项目(201003009,20090460145),中央高校基本科研业务费(201012200053),湖南省科技计划项目(2010DFJ411)和中南大学理科发展基金(08SDF02,09SDF09)资助