退火条件对山梨醇玻璃焓松弛参数的影响

叶 斌 高 才 刘向农 杨 锁 江 斌

(合肥工业大学机械与汽车工程学院,合肥230009)

退火条件对山梨醇玻璃焓松弛参数的影响

叶 斌 高 才*刘向农 杨 锁 江 斌

(合肥工业大学机械与汽车工程学院,合肥230009)

采用差示扫描量热法(DSC)测定山梨醇样品经历不同时间(ta)等温退火后,以10 K·min-1速率进行升温时玻璃化转变温度(Tg)前后的比热容(Cp(T)).将Gómez Ribelles(GR)提出的一种基于构型熵的现象学模型用于描述山梨醇玻璃的焓松弛行为,考察GR模型能否适用于小分子玻璃体系.结果表明,单组GR模型参数拟合的曲线均能较好重现对应热历史条件下的山梨醇体系的实验所得Cp(T)曲线,尽管并未找到不随热历史而变的一组参数作为材料常数,但与其它现象学模型应用于小分子玻璃时,其模型参数都随热历史变化而变化的特点相比,GR模型的某些参数基本保持不变.且在较长退火时间下拟合得到的模型参数普适性较好.同经历连续降温的山梨醇相比,等温退火过程得到的松弛极限态参数(δ)的平均值与Tg处比热容增量(ΔCp(Tg))的比值明显增大,但仍小于聚合物的值,表明GR模型提出的亚稳极限态对小分子玻璃的影响值得商榷.

焓松弛;差示扫描量热法;构型熵;山梨醇;玻璃化转变;等温退火;脆度

1 引言

玻璃化转变是玻璃态与橡胶态之间的转变,可看成是较长分子(或链段)运动的“冻结”或“解冻”过程,对应温度称为玻璃化转变温度(Tg).1玻璃态物质多处于热力学非平衡态,在Tg温度以下会逐渐向平衡态转变,体系的热力学性质(焓、热膨胀系数)以及力学性质(模量、力学损耗)也随之发生连续变化,称之为结构松弛,当采用焓的变化来描述结构松弛时则称为焓松弛.2有许多实验方法可研究这一现象,其中以差示扫描量热法(DSC)应用最为广泛,它是通过获取一定升温速率下跨越玻璃化转变区域的比热容,推测体系之前所经历的复杂热历史及微观位形的演变,为合理使用材料提供科学依据.3,4一些现象学模型可以较好地描述玻璃化体系的转变和松弛行为,代表性的有Tool-Narayanaswamy-Moynihan (TNM)5-7和Adam-Gibbs-Voegel(AGV)8,9模型,二者均使用假想温度Tf来表征体系的结构演变,5只是特征松弛时间的表达有所差异.尽管两个模型能很好地重现玻璃化体系的升温比热容,但模型参数有时不是材料常数,而是随体系热历史的不同而变化.此外,这两个模型都假定只要时间足够长,玻璃态最终会松弛到对应温度的平衡态,但迄今未被实验所证实.5-9Gómez Ribelles(GR)等10,11在Adam-Gibbs(AG)8协同松弛理论基础上,摈弃了传统现象学模型中用假想温度表征结构演变的做法,而是提出用构型熵演变表征体系结构的变化.12-15不仅如此,该模型还假设玻璃态不能最终松弛到对应温度的平衡态,而只能松弛到某一中间亚稳极限态.由于聚合物是链状大分子的缘故,中间亚稳极限态理论的提出确实使GR模型预测聚合物焓松弛的能力有了明显提高,13-15近年来该模型在聚合物玻璃的松弛动力学研究中也得到广泛应用,16-22但迄今为止尚未见到有人将此模型用于研究聚合物玻璃以外的体系,尤其是对于小分子玻璃体系而言是否也存在这样的一个亚稳极限态还不得而知,也并未有相关文献来说明.本文正是为研究GR模型中提出的亚稳极限态是否适用于小分子玻璃而展开的.在稍早的工作中,我们已将此模型用于研究无定形山梨醇体系经历连续降温的情形,23结果表明GR模型能很好地重现山梨醇不同降温速率下Cp(T)曲线,且某些模型参数表现出不随热历史的变化而变化的特征,相对于其他模型改进效果明显.但物质的热历史不仅包括经历不同降温速率,还应包括退火(物理老化),由于现实中这种现象较连续降温更为常见,因此考察等温退火条件下山梨醇玻璃的松弛特性和GR模型参数可能展现的新特征,现实意义更为明确.

GR模型是在Kohlrausch-Williams-Watts(KWW)和AG描述的传统理论的基础上,提出用构型熵(Sc)替代TNM和AGV模型中的假想温度Tf来表征体系的结构演变,并设想玻璃态物质在时间t→∞时并不能松弛到过冷液体线性外推的平衡态,而只能松弛到依温度而变的另一假想的极限态(如图1所示).

如用Sclim() T表示此极限态构型熵,并用T(ξ)(其中ξ满足-∞＜ξ≤t)表示温度历史,将温度历史表示为

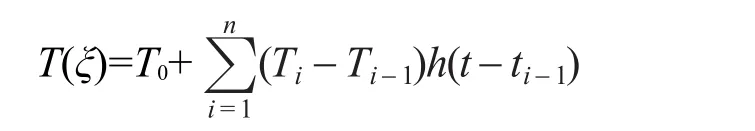
h为单位阶跃函数,则构型熵Sc(t)可表示:10

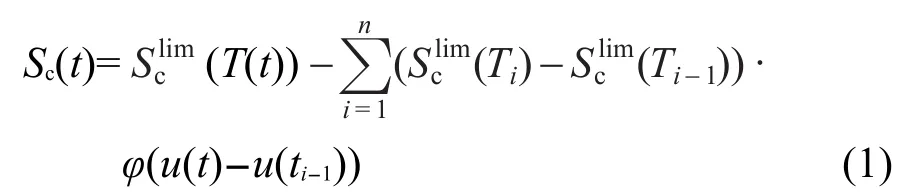
φ(u)是松弛函数(也称衰减函数),可用KWW延展指数函数得到:

β是表征体系松弛时间谱分布宽度的非指数参数(0≤β≤1),u(t)为约化时间:6

τ(σ)是特征松弛时间,由σ时刻的构型熵(Sc)和温度(T)共同决定.由AG协同松弛理论:

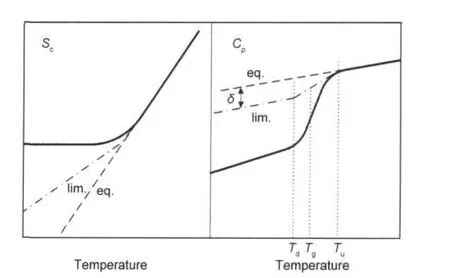
图1 基于构型熵的焓松弛模型中松弛极限态示意图12Fig.1 Scheme of the hypothetical limit state in the enthalpy relaxation model based on the configurational entropy12Sketch of the configurational entropy corresponding to the equilibrium liquid state(eq.)(dashed line),to an experimental cooling scan at a finite cooling rate(solid line),and to the metastable line of the hypothetical limit states of the structural relaxation process(lim.) (dashed-dotted line).Tg:glass transition temperature, Td:Tg+5,Tu:Tg+10

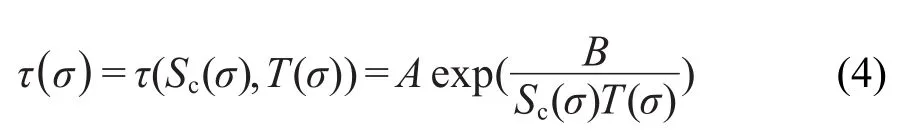
其中A是指前因子,可看成是体系在无限高温度下的松弛时间;B=Sc*Δμ/k,Sc*表示最小协同重排域的位形熵;Δμ表示阻止单体(链段或分子)协同重排的能量势垒,k是Boltzmann常数.

在Tg以上,极限构型熵与平衡态相同:

其中位形比热容ΔCp(T)=Cpl(T)−Cpg(T),Cpl(T)和Cpg(T)分别表示过冷液体与玻璃的比热容;T2是Gibbs-Dimarzio转变温度;θ为积分变量.24

在玻璃化转变区及Tg以下,极限构型熵可表示为:

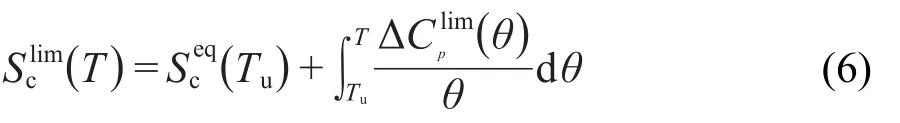
其中Tu是Tg以上的某一温度(通常取Tu=Tg+10).

借鉴Hodge等25的做法,由以上各式可得经历等温退火后的构型熵表达:

其中ta为退火时间,nA(nA≤n≤nA+10)是开始退火子步,当 k=nA+1时,Δta,k=t110a;当k＞nA+1时,Δta,k=

Gómez Ribelles12通过定义构型焓(Hc)建立构型熵和比热容的关联:

由图1可知玻璃态斜率dSlimc(T)/dT=(ΔCp(T)-δ)/T,故该模型中共有A,B,β,T2,δ五个待求参数,可用曲线拟合方法确定,并通过最优搜索使模型预测的Cp(T)曲线和DSC测定的结果最接近.

2 实验部分

2.1 试剂与仪器

结晶态山梨醇(瑞士Fluka,纯度99%,合肥森瑞科贸有限公司进口分装)未经进一步纯化,置于常温、压力40 Pa的真空干燥箱中干燥24 h后备用.取样品5-10 mg(精确到±0.01 mg)置于标准液体铝皿中央并压盖密封.采用配备G-M二级制冷系统的DSC仪器(Pyris-Diamond,美国Perkin-Elmer公司),标称最低温度193 K,实测DSC内样品温度最低可达约200 K.DSC以金属铟(99.999%,Perkin-Elmer)和纯水(自制二次蒸馏去离子水)做两点温度标定,标定范围210-320 K;以冰的融化潜热(333.88 J·g-1)进行单点焓尺度标定,标定速率10 K·min-1.氮气(99.999%)气氛,流量约25 mL·min-1,并保持恒定.

2.2 DSC实验流程

山梨醇晶体以10 K·min-1的速率升温至388 K充分熔融后降温至Tg(267.5 K左右)以下,结果表明,熔融态的山梨醇不再形成结晶体,而是形成完全的玻璃态.

等温退火实验流程如图2所示,先将玻璃态样品升温至加样温度303.15 K后,以10 K·min-1的降温速率降至Ta=253.15 K等温退火(退火时间ta分别为10、30、60、120、240、480 min),再以10 K·min-1继续降温至218.15 K,待热流稳定后按如下温度程序采集数据:(1)等温1 min;(2)以10 K·min-1速率升温到308.15 K;(3)等温1 min.取和样品皿质量相同的空皿(±0.01 mg),骤冷至218.15 K,热流稳定后,按与分析样品相同的温度程序获得基线热流,用于比热容计算,为保证热接触状况的一致性,针对一个样品的所有分析结束后再获得一条用于计算比热容的基线.

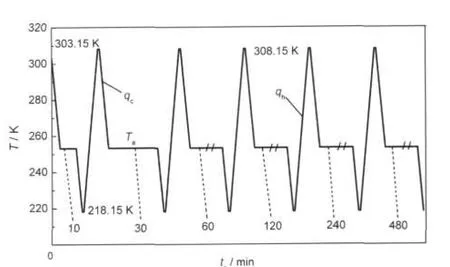
图2 测量不同退火时间(ta)的等温退火焓松弛的实验程序Fig.2 Schematic representation of the experimental procedure for measuring the isothermal annealing enthalpy relaxation with different annealing time(ta)qc(cooling rate)=10 K·min-1,qh(heating rate)=10 K·min-1, Ta=253.15 K

2.3 曲线拟合及误差分析

曲线拟合程序以Matlab®语言编制,采用Nedler-Mead搜索方法26寻求最优参数,使模型与实验数据之间拟合的均方差最小:

式中i是实验次数,j是实验扫描时的温度点,w(i)为权重因子.最优搜索可以通过固定T2或者B来实现,将B置于循环之外来进行处理.数据误差主要来自如下3方面:(1)平行样间误差;(2)DSC重复性误差;(3)曲线拟合误差.分析结果表明,曲线拟合误差最大.

3 结果和讨论

3.1 结 果

图3 不同退火时间下山梨醇在Tg附近的比热容曲线(a)以及与参照比热容之差(b)Fig.3 Specific heat capacity curves near Tgat different annealing time for D-sorbitol(a)and difference between the Cp(T)curves of the reference scan(b)

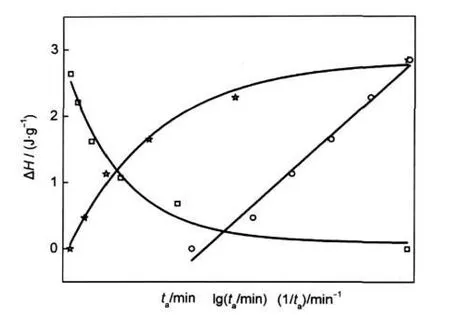
图4 253.15 K时恢复焓ΔH与ta的关系Fig.4 Recovery enthalpy ΔH as a function of the annealing time for D-sorbitol annealing at 253.15 KΔH-ta(☆),ΔH-1/ta(□),ΔH-lgta(○)

采用DSC测定的山梨醇玻璃在Tg前后的比热容曲线如图3(a)所示.观察发现,经历不同ta的山梨醇在玻璃化转变区域的高温侧皆呈现α松弛所引起的明显焓恢复峰,且随ta的增加,比热容最大值Cp_max增加明显,峰的右移效果显著.在进行恢复焓计算时,需预先获取一条未发生明显松弛体系的比热容曲线作为参照.由于ta越小,其松弛效应越不显著,故选择ta=10 min的比热容曲线作为参考曲线Cp,ref,计算结果如图3(b)所示,同连续降温相比,热流“下冲”现象显著.图4表示实验得到的恢复焓ΔH与ta关系,观察发现随ta增加,ΔH起始增加显著,随后趋于平缓,说明此时山梨醇玻璃接近亚稳极限态,由ΔH-1/ta关系外推可求得山梨醇玻璃在t→∞时,恢复焓极限值ΔH∞约为3.11 J·g-1,ΔH与lgta基本呈线性关系.

表1列出由DSC实验读取的恢复焓,及按不同读取方法27获得的Tg.此前针对山梨醇连续降温的实验结果23表明,随降温速率的增加,极限假想温度Tf′逐渐增加,而其余读法则无规律.而由表1可知,随ta的增加,Tf′逐渐减小,其余读法的温度则是单调递增.比较发现,等温退火实验得到的Tf′略低于Duvvuri等28利用介电法的分析结果(267.5 K).尽管退火时间的不同可能会导致体系微观结构和松弛程度的差异,但表1结果显示,松弛并未引起比热容增量ΔCp(Tg)的明显变化.玻璃化转变过程中ΔCp(Tg)被称为热力学脆度,它的大小表明了玻璃在升温过程中自由度的释放程度,值越大,则由玻璃态转变为过冷态后,松弛单元获得的活动性越大,29等温退火实验得到的ΔCp(Tg)值保持在0.94 J·g-1·K-1,与连续降温实验23的ΔCp(Tg)=0.99 J·g-1·K-1相比,稍低.

3.2 讨 论

同TNM和AGV模型相比,GR模型引入了新参数δ,进一步增加了曲线拟合的难度.尽管GR模型无需使用无量纲比热容,减少了无量纲化造成的误差,但与TNM模型25,30,31和Scherer-Hodge模型9,30,32-34相似,GR模型参数A、B、T2和β之间依然存在相关性,10-12全参数拟合的结果难以找到全局最优解.故需在拟合中人为选定某一参数后求取其他参数.目前除了Théneau等17选择A及Andreozzi等34-36选择T2以外,其余均是将B作为可选参数,如Brunacci等37在B=500-3000 J·g-1的范围内获取了聚苯乙烯的GR模型参数,Gómez Ribelles等10在B=1000-2000 J·g-1的范围内获取了聚碳酸酯的GR模型参数, Meseguer Dueñas等13在B=500-1500 J·g-1的范围内获取了丙烯腈共聚物的GR模型参数.由于同聚合

物相比,其它模型参数随B值的变化相对缓慢,因此在曲线拟合程序中将B值选取在一个更宽的范围(500-5000 J·g-1)内.结果表明,当B在500-5000 J· g-1范围内,GR模型均能很好地重现DSC实验测得的升温比热容曲线.拟合得到的GR模型参数如表2所示.图5给出B=3000 J·g-1时不同ta下GR模型预测Cp值与实验数据的比较结果(其它参数见表2).显然,针对单条实验Cp(T)曲线,计算程序始终能找到一组与之对应的GR模型参数,使得模型预测值和实验值相吻合.

表1 不同ta下山梨醇玻璃化转变温度(Tg)和焓恢复参数Table 1 Glass transition temperature(Tg)and enthalpy recovery parameters of D-sorbitol at different annealing time

表2 曲线拟合方法得到的不同退火时间山梨醇玻璃GR模型参数Table 2 GR model parameters of D-sorbitol glass at different annealing time obtained using curve-fitting method

假设液态与玻璃态的比热容与温度之间存在线性关系,对ΔCp(T)来说这种线性关系依然存在,在GR模型中常表示为温度T的线性函数.如取6条实验曲线的平均值,可得到:

由于A2为负值,因此在Tg之上的某一个温度(T≈935 K),ΔCp=0.Hodge在AGV模型9中使用双曲关系ΔCp(T)=ΔCp(Tg)Tg/T计算ΔCp,随T的增加,ΔCp减小,但它并不会等于零.由表1可知两种方法计算结果基本相同.

Moynihan等7提出利用极限假想温度随降温速率的依变关系确定松弛活化焓

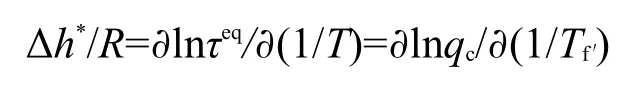
由连续降温实验结果得到Δh*/R=79.258×103K.根据Angell38,39提出的动力学脆度计算公式:

得到m≈128.6,这与介电松弛分析得到的结果(m≈127.0)28非常吻合.根据公式(4)可推知:

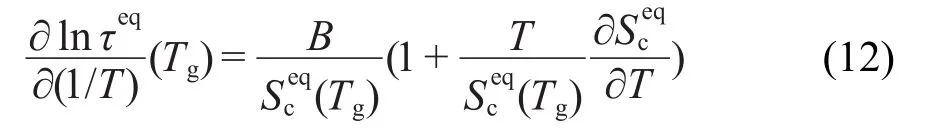
由公式(5)、(10)、(11)、(12)及表2数值,计算各种ta下不同B对应动力学脆度m,结果见表2.观察发现,当B≤4000 J·g-1,随ta增加,相同B值对应的m逐渐减少,而B=5000 J·g-1时,m的变化则毫无规律.此前文献40发现采用TNM模型拟合的松弛活化焓要小于变降温速率实验计算得到的结果,但是这一现象在应用GR模型描述经历等温退火热历史的山梨醇玻璃时得到改观.表2的脆度计算结果表明,多种状况下m＞128.6.B=3000 J·g-1时,脆度平均值mmean约为129.2,和式(11)及介电松弛的分析结果吻合.同时也发现,不同退火时间下,B=3000 J·g-1时,Tg-T2的平均值约为51.1 K,这也与大多数玻璃化物质这一结论41吻合.

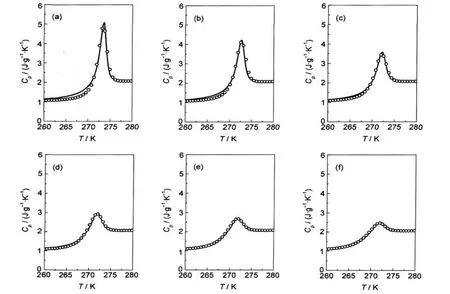
图5 山梨醇实验(○)与GR模型预测(－)的比热容(Cp)曲线Fig.5 Curves of specific heat capacities(Cp)of experimental data(○)and GR fits(－)for D-sorbitolB=3000 J·g-1,the remaining parameters of GR model as shown in Table 2.ta/min:(a)480,(b)240,(c)120,(d)60,(e)30,(f)10

图6 GR模型预测(－)与山梨醇实验(○)的比热容(Cp)曲线对照Fig.6 Comparison between some of the predictions of the GR model(－)and the experimental scans(○)parameters obtained for D-sorbitolthe GR model parameters at(a)ta=10 min,B=3000 J·g-1,-ln(A/s)=46.78,T2=213.6 K,β=0.510,δ=0.281 J·g-1·K-1; (b)ta=480 min,B=3000 J·g-1,-ln(A/s)=42.70,T2=209.7 K,β=0.372,δ=0.0125 J·g-1·K-1

由表2可知,与已报道过的某些聚合物12,13的参数δ基本保持不变(且普遍较大)的特点不同,经历等温退火热历史后的山梨醇的δ是在一定范围(0.001-0.464 J·g-1·K-1)内波动.B=3000 J·g-1时山梨醇玻璃δ的平均值为0.107 J·g-1·K-1,约为ΔCp(Tg)的11.4%.连续降温过程中B=4000 J·g-1时δ的平均值为0.021 J·g-1·K-1,约为ΔCp(Tg)的2.0%,对比发现等温退火条件下得到的δ明显偏大,可以推断对于山梨醇玻璃体系而言,等温退火条件下的亚稳松弛极限态要更远离平衡液态外推对应的平衡态,但是仍然要小于某些聚合物的δ值,这也许是因为聚合物是链状大分子的缘故,所以受亚稳态极限参数δ的影响较大,但对小分子山梨醇玻璃体系来说,GR模型所提出的亚稳极限态概念的影响还值得进一步探讨.

现象学模型参数须为材料常数,即与体系经历的热历史无关,13图5显示单组拟合参数能很好地重现对应热历史的实验Cp(T)曲线,但这组参数是否适用于其它热历史尚不清楚.如果其中的某组参数能够较好地重现所有热历史的DSC实验曲线,则可将其近似看成不依赖于热历史的材料常数.但表2中无法找到这样一组参数,只是B=3000 J·g-1时,-lnA和T2变化不大,可看成是材料常数,而β值则随ta的增加而逐渐减小,且变化幅度较大.但通过用不同退火时间下的模型参数来预测其它实验条件下比热容曲线,可以发现用GR模型对经历等温退火热历史山梨醇的焓松弛行为进行描述时,哪种实验条件下得到的模型参数的预测力更好.图6表示B=3000 J· g-1时(其它B值结果相同,未列出)分别将ta=10 min和ta=480 min的两组GR参数(其余参数见表2)看成材料常数后用来预测其它退火时间实验比热容的结果.观察发现较短退火时间拟合得到的模型参数普适性较差,用来预测其它热历史的效果不能令人满意,而反之效果稍微好一些,至少峰形和台阶变化不大.总体来说将GR模型应用在山梨醇玻璃焓松弛行为研究过程中也并不能发现一组确定的模型参数可以作为不依赖于热历史的材料常数,但是考虑到TNM和AGV模型应用于多元醇玻璃体系时,其模型参数都随热历史的变化而变化,27,42而GR模型中某些参数值基本保持不变,这一点值得肯定.

4 结论

采用DSC技术结合GR模型考察了经历不同退火时间的山梨醇玻璃的焓松弛行为.由实验数据可推知,当退火时间无限长时,山梨醇的恢复焓极限值为3.11 J·g-1.拟合结果表明单组GR模型参数能很好地重现对应热历史条件下的山梨醇体系的实验比热容,但也并未找到一组模型参数能作为材料常数,但B为3000 J·g-1时,-lnA和T2的变化并不明显,与TNM和AGV模型的四个参数都在变化相比,GR模型已经有了很大的改善.且观察发现,采用较长退火时间的GR模型参数对较短退火时间的实验升温比热容进行预测时,效果稍好一些.与连续降温过程相比,松弛极限态参数δ值增加显著,可判定等温退火条件下的山梨醇玻璃体系亚稳极限态更加远离过冷液体外推平衡态,但仍低于某些聚合物的相应值.尽管GR模型提出的亚稳极限态用在小分子玻璃上确实有值得商榷的地方,但采用GR模型拟合得到的山梨醇动力学脆度参数与介电松弛分析得到的结果却很吻合.

(1) Lebrun,N.;van Miltenburg,J.C.J.Alloy.Compd.2001,320, 320.

(2) Hodge,I.M.J.Non-Cryst.Solids 1994,169,211.

(3) Hutchinson,J.M.;Kumar,P.Thermochim.Acta 2002,391,197.

(4)Cameron,N.R.;Cowie,J.M.G.;Ferguson,R.;McEwan,I. Polymer 2000,41,725.

(5)Tool,A.Q.J.Am.Ceram.Soc.1946,29,240.

(6)Narayanaswamy,O.S.J.Am.Ceram.Soc.1971,54,491.

(7) Moynihan,C.T.;Easteal,A.J.;DeBolt,M.A.;Tucker,J.J.Am. Ceram.Soc.1976,59,12.

(8)Adam,G.;Gibbs,J.H.J.Chem.Phys.1965,43,139.

(9) Hodge,I.M.Macromolecules 1987,20,2897.

(10) Gómez Ribelles,J.L.;Monleón Pradas,M.Macromolecules 1995,28,5867.

(11) Gómez Ribelles,J.L.;Monleón Pradas,M.;Vidaurre Garayo, A.;Romero Colomer,F.;Más Estellés,J.;Mese-guer Dueñas,J. M.Macromolecules 1995,28,5878.

(12) Gómez Ribelles,J.L.;Monleón Pradas,M.;Vidaurre Garayo, A.;Romero Colomer,F.;Más Estellés,J.;Meseguer Dueñas,J. M.Polymer 1997,38,963.

(13)Meseguer Dueñas,J.M.;Vidaurre Garayo,A.;Romero Colomer,F.;Más Estellés,J.;Gómez Ribelles,J.L.;Monleón Pradas,M.J.Polym.Sci.Part B:Polym.Phys.1997,35,2201.

(14) Gómez Ribelles,J.L.;Vidaurre Garayo,A.;Cowie,J.M.G.; Ferguson,R.;Harris,S.;McEwen,I.J.Polymer 1998,40,183.

(15) Cowie,J.M.G.;Harris,S.;Gómez Ribelles,J.L.;Meseguer,J. M.;Romero,F.;Torregrosa,C.Macromolecules 1999,32,4430.

(16) Tanaka,Y.Polym.J.2009,41,125.

(17) Théneau,C.;Salmerôn Sánchez,M.;Rodríguez Hernández,J. C.;Monleón Pradas,M.;Saiter,J.M.;Gómez Ribelles,J.L. Eur.Phys.J.E 2007,24,69.

(18) Mano,J.F.;Gómez Ribelles,J.L.;Alves,N.M.;Salmerôn Sánchez,M.Polymer 2005,46,8258.

(19)Alves,N.M.;Gómez Ribelles,J.L.;Manoa,J.F.Polymer 2005, 46,491.

(20) Salmerôn Sánchez,M.;Touzé,Y.;Saiter,A.;Saiter,J.M.; Gómez Ribelles,J.L.Colloid Polym.Sci.2005,283,711.

(21)Andreozzi,L.;Autiero,C.;Faetti,M.;Galli,G.;Giordano,M.; Zulli,F.Macromol.Rapid Commun.2008,29,928.

(22)Hernández Sánchez,F.;Meseguer Dueñas,J.M.;Gómez Ribelles,J.L.J.Therm.Anal.Cal.2003,72,631.

(23) Gao,C.;Chen,K.S.;Ye,B.;Yang,S.;Liu,X.N.;Jiang,B.Acta Chim.Sin.2011,69,37. [高 才,陈开松,叶 斌,杨 锁,刘向农,江 斌.化学学报,2011,69,37.]

(24) Gibbs,J.H.;DiMarzio,E.A.J.Chem.Phys.1958,28,373.

(25) Hodge,I.M.;Berens,A.R.Macromolecules 1982,15,762.

(26) Nedler,J.A.;Mead,R.Comput.J.1965,7,308.

(27) Gao,C.;Yang,S.;Liu,X.N.;Wang,T.J.;Jiang,B.Acta Phys.-Chim.Sin.2010,26,453. [高 才,杨 锁,刘向农,王铁军,江 斌.物理化学学报,2010,26,453.]

(28) Duvvuri,K.;Richert,R.J.Phys.Chem.B 2004,108,10451.

(29)Huang,D.;MacKenna,G.B.J.Chem.Phys.2001,114,5621.

(30) Gómez Ribelles,J.L.;Ribes Greus,A.;Diaz Calleja,R. Polymer 1990,31,223.

(31) Moynihan,C.T.;Crichton,S.N.;Opalka,S.M.J.Non-Cryst. Solids 1991,131-133,420.

(32) Romero Colomer,F.;G6mez Ribelles,J.L.Polymer 1989,30, 849.

(33) Hodge,I.M.J.Non-Cryst.Solids 1991,131-133,435.

(34)Andreozzi,L.;Faetti,M.;Giordano,M.;Palazzuoli,D.J.Non-Cryst.Solids 2003,332,229.

(35)Andreozzi,L.;Faetti,M.;Zulli,F.;Giordano,M.Eur.Phys.J.B 2004,41,383.

(36)Andreozzi,L.;Faetti,M.;Giordano,M.;Palazzuoli,D. Macromolecules 2002,35,9049.

(37) Brunacci,A.;Cowie,J.M.G.;Ferguson,R.Macromolecules 1996,29,7976.

(38) Angell,C.A.Science 1995,267,1924.

(39) Ediger,M.D.;Angell,C.A.;Nagel,S.R.J.Chem.Phys.1996, 100,13200.

(40) Wungtanagorna,R.;Schmidst,S.J.Thermochim.Acta 2001, 369,95.

(41) Williams,M.L.;Landel,R.F.;Ferry,J.D.J.Am.Chem.Soc. 1955,77,3701.

(42) Gao,C.;Wang,T.J.;Liu,X.N.;Zhou,G.Y.;Hua,T.C.Chin.J. Chem.Phys.2007,20,258.

November 8,2010;Revised:December 29,2010;Published on Web:March 8,2011.

Effect of Annealing Conditions on Enthalpy Relaxation Parameters of D-Sorbitol Glass

YE Bin GAO Cai*LIU Xiang-Nong YANG Suo JIANG Bin
(School of Mechanical and Automotive Engineering,Hefei University of Technology,Hefei 230009,P.R.China)

We studied the enthalpy relaxation dynamics of amorphous D-sorbitol by differential scanning calorimetry(DSC).A series of specific heat capacities(Cp(T))for D-sorbitol were measured upon heating of 10 K·min-1.The samples were subjected to thermal treatment involving isothermal annealing with different annealing time(ta).A new phenomenological model by Gómez Ribelles(the GR model)of enthalpy relaxation based on the evolution of configurational entropy was used to simulate the experimental data to verify the applicability of the GR model to small molecular glass.The results indicated that a single set of GR model parameters only reproduced the corresponding experimental Cp(T)curve of D-sorbitol fairly well. It failed to find a set of GR model parameters as the material constant independent of the thermal history.In contrast with other phenomenological models,some parameters of the GR model remained unchanged. The model parameter sets obtained under longer annealing time show better predictive ability.In contrast to the continuous cooling process for D-sorbitol,the ratio between the mean value of the limit state parameter(δ)and the increment of specific heat capacity at Tg(ΔCp(Tg))apparently increases,but the increase is less than that of polymers.The results brought into question if the metastable limit state introduced by the GR model applied to small molecular glass systems.

Enthalpy relaxation;Differential scanning calorimetry;Configurational entropy; D-sorbitol;Glass transition;Isothermal annealing;Fragility

O642

*Corresponding author.Email:gao_cai@hotmail.com;Tel:+86-13721029540.

The project was supported by the National Natural Science Foundation of China(20803016)and Natural Science Foundation ofAnhui Province, China(070414163).

国家自然科学基金(20803016)和安徽省自然科学基金(070414163)资助项目