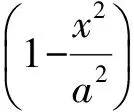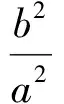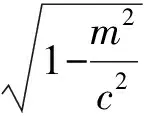对杯中球问题的探究与推广
●(华中师范大学数学与统计学学院 湖北武汉 430079)
对杯中球问题的探究与推广
●李俊杰(华中师范大学数学与统计学学院 湖北武汉 430079)

图1
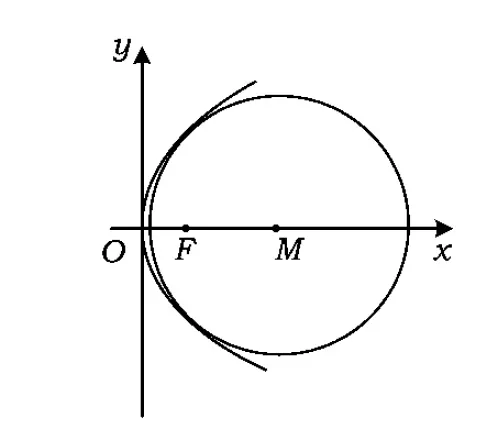
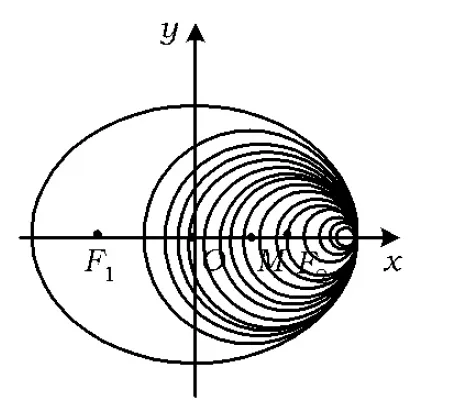
在抛物线形高脚杯中放进球形物体,当球的半径不同时,球可以碰到杯底,也可以卡在杯口上,这就是杯中球问题[1],其数学模型如图1所示.
杯中球问题实质上是一个最短距离问题:在抛物线内部,求抛物线对称轴上的点到抛物线的最短距离.
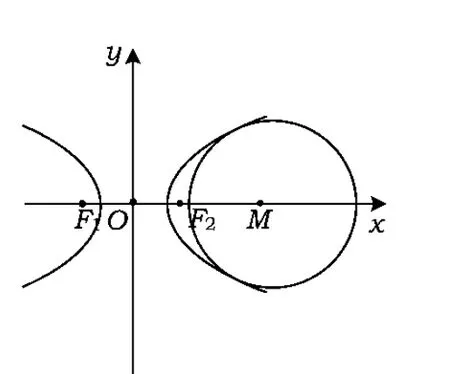
性质1[1]设抛物线方程为y2=2px(p>0),点M(m,0)(m>0).
(1)当0 文献[1]以开口向上的抛物线为例进行了证明,笔者不再赘述. 推论1[1]设抛物线方程为y2=2px(p>0),点M(m,0)(m>0),在抛物线内作以点M为圆心的内切圆. (1)当0 (2)当m>p时,圆与抛物线有2个切点,如图3所示. 图2 图3 受杯中球问题的启发,笔者也对椭圆和双曲线进行了类似的探究,横向拓展得出了以下结论. (1)当m∈(-a,-ce]∪[ce,a)时,点M到椭圆的最短距离为a-|m|; 证明设P(x,y)为椭圆上任意一点,则 |MP|2=(x-m)2+y2= e2x2-2mx+m2+b2= 故当m∈(-a,-ce]∪[ce,a)时,|MP|min=a-|m|. (1)当m∈(-a,-ce]∪[ce,a)时,圆与椭圆有唯一切点,且切点为椭圆长轴的端点,如图4所示; (2)当m∈(-ce,ce)时,圆与椭圆有2个切点,如图5所示. 图4 图5 (1)当m∈[-ce,-a)∪(a,ce]时,点M到双曲线的最短距离为|m|-a; 证明设P(x,y)为双曲线上任意一点,则 m∈[-ce,-a)∪(a,ce]. 当m∈(a,ce]时,f(x)在x=a处取得最小值,此时 |MP|min=|a-m|=m-a; 当m∈[-ce,-a)时,f(x)在x=-a处取得最小值,此时 |MP|min=|-a-m|=-m-a, 故当m∈[-ce,-a)∪(a,ce]时, |MP|min=|m|-a. m∈(-∞,-ce)∪(ce,+∞). (1)当m∈[-ce,-a)∪(a,ce]时,圆与双曲线有唯一切点,且切点为双曲线的顶点,如图6所示; (2)当m∈(-∞,-ce)∪(ce,+∞)时,圆与双曲线有2个切点,如图7所示. 图6 图7 经常讨论焦点到圆锥曲线的最短距离问题,文献[1]中已得出相关结论:圆锥曲线上到焦点距离最近的点为其对应顶点,即以焦点为圆心,与之较近顶点连线为半径的圆必内切于该圆锥曲线,顶点为切点.实际上,文献[2]是本文的一个特例,本文是文献[2]更一般的结论. [1] 蒋声,陈瑞琛.趣味解析几何[M].上海:上海教育出版社,2007:283-285. [2] 任志瑜.更应该站在学生的角度来处理教材[J].数学通讯,2010(9):31-34.