赋范空间关于强变分不等式的α-例外簇

韦丽兰, 黄力人

(华南师范大学数学科学学院,广东广州 510631)

变分不等式理论是当今非线性分析的重要组成部分,它在力学、微分方程、控制论、数理逻辑、对策论和非线性规划等理论和应用学科都有广泛的应用.

(1)

(2)

研究变分不等式问题和非线性互补问题的一个基本问题是讨论解的存在性.研究变分不等式问题和非线性互补问题解的存在性有很多方法,例如Browder不动点定理、KKM定理、拓扑度理论和强制性条件等.

SMITH在文献[2]中引入“例外序列”的概念来研究非线性互补问题解的存在性问题,但只限于K=的情形.ISAC注意到例外序列和拓扑度的联系,在文献[3]中提出例外簇的概念并借助拓扑度的理论来研究一般非线性互补问题解的存在性.

在例外簇概念提出以后,很多学者用例外簇的概念研究变分不等式问题和非线性互补问题解的存在性,使例外簇概念得到了丰富和发展,可参见文献[1]、[4]-[14].ISAC和ZHAO[4]首次把例外簇的概念从n空间推广到更一般的无限维Hilbert空间.2006年,BIANCHI[1]等在赋范空间中引入一个强变分不等式SVIP的例外簇的概念,推广了文献[12]和文献[13]例外簇的概念.

本文的第2部分给出一些定义和基本概念.第3部分在赋范空间中提出一个强变分不等式SVIP的α-例外簇的概念,推广文献[1]所给出的例外簇的概念,并给出相应的解的存在性定理,得到择一型“强变分不等式或者有解,否则存在一个α-例外簇”.

1 预备知识

正规对偶映射J:X→2X*定义如下:

注1[1]若X是Hilbert空间H,记H=H*,则J(x)=x.

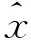
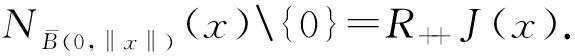
即

于是

因此,〈x*,x〉≥‖x*‖‖x‖.另一方面,〈x*,x〉≤‖x*‖‖x‖.所以

〈x*,x〉=‖x*‖‖x‖.

(3)

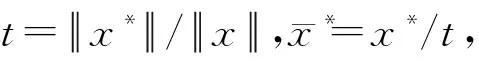
〈x*,y〉≤‖x*‖‖y‖≤‖x*‖‖x‖=〈x*,x〉.

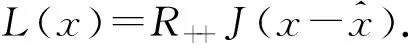
2 主要结果

下面给出文献[1]中例外簇的定义.

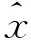
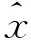
注2 BIANCHI在文献[1]中研究0-例外簇.

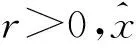
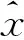
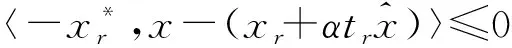
(4)

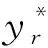
(5)

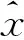
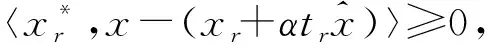
(6)

由条件(d4)和tr>0,有

(7)

参考文献：

[1] BIANCHI M,HADJISAVVAS N,SCHAIBLE S.Exceptional families of elements for variational inequalities in Banach spaces[J].J Optim Theory Appl,2006,129(1):23-31.

[2] SMITH T E.A solution condition for complementarity problems,with an application to spatial price equilibrium[J].Appl Math Computation,1984,15:61-69.

[3] ISAC G,BULAVASKI V,KALLSHNIKOV V.Exceptional families,topological degree and complementarity problems[J].J global optim,1999,14(2):207-225.

[4] ISAC G,ZHAO Y B.Exceptional family of elements and the solvability of variational inequalities for unbounded sets in infinite dimensional Hilbert spaces[J].J Math Anal Appl,2000,246:544-556.

[5] DANIILIDIS A,HADJISAVVAS N.Coercivity conditions and variational inequalities[J].Math Program,1999,86:433-438.

[6] CROUZEIX J P.Pseudomonotone variational inequality problems:existence of solutions[J].Math Programming,1997,78(3):305-314.

[7] AUSSEL D,HAOJISAVVAS N.Technical note on quasimonotone variational inequalities[J].J Optim Theory Appl,1999,102(2):475-495.

[8] ZHANG L P,HAN J Y,XU D C.Existence theorems of solution to variational inequality problems[J].Sci China Ser A,2001,44(2):212-219.

[9] BIANCHI M,HADJISAVVAS N,SCHAIBLE S. Minimal coercivity conditions and exceptional families of elements in quasimonotone variational inequalities[J].J Optim Theory Appl,2004,122(1):1-17.

[10] ZHOU S Z,BAI M R.A new exceptional family of elements for a variational inequality problem on Hilbert space[J].Appl Math Lett,2004,17:423-428.

[11] TAN L,HUANG L.Exceptional families of elements for a variational inequality problem [J].Appl Math Lett,2007,20:599-604.

[12] ISAC G,KALLSHNIKOV V.Exceptional family of elements,Leray-Schauder alternative,pseudomonotone operatora,and complementarity[J].J Optim Theory Appl,2001,109:69-83.

[13] HAN J,HUANG Z H,FANG S C.Solvability of variational inequality problems[J].J Optim Theory Appl,2004,122:501-520.

[14] 谭露琳.空间中变分不等式问题解的存在性与例外簇[J].华南师范大学学报:自然科学版,2009(3):22-24.

TAN Lulin.Exceptional families of elements for a variational inequality problem on Hilbert space[J].South China Normal University:Natural Science Edition,2009(3):22-24.

[15] AUBIN J P,EKELAND I.Applied nonlinear analysis[M].New York:John Wiley and Sons,1984.