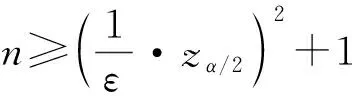作业时间服从指数分布的调度规则失效率分析
汤健超,张国基,张毕西,林彬彬
(1.华南理工大学计算机科学与工程学院,广东广州 510641;2. 华南师范大学计算机学院,广东广州 510631;3. 华南理工大学数学科学学院, 广东广州 510641;4.广东工业大学管理学院,广东广州 510520)
作业调度的研究具有重要的理论意义和工程价值,由于许多作业计划调度问题已被证明是NP完全问题,求解此类问题的精确解,对于中等规模情形时的计算时间已超出人们能接受的范围.因此,现在通常通过各种启发式的方式,试图求解问题的较优解.
在各种调度规则中,有一类是基于工序时间的调度规则,如最小时间规则(SPT)、最大时间规则(MPT)、最短剩余加工时间规则(SRPT)、最小松弛时间规则(SL/OP)等[1-2].这一类规则,调度决策的参数基于参数的预计值,通常为参数的期望.而实际作业时间是波动的,因此调度结果可能会与调度目标背离.如根据SPT规则,预计工序时间E(TB)
但是,目前对在作业呈现随机波动的情况下,对调度规则失效率展开定量分析的研究较少.1998年,学者在作业时间分布呈三角状时,分析了2项工作时调度规则的失效性.在2002年有学者进一步分析了在作业时间服从正态分布的情况下,对于2项工作和3项工作时采用SPT规则的调度规则的失效率,同时分析了其敏感性[3].
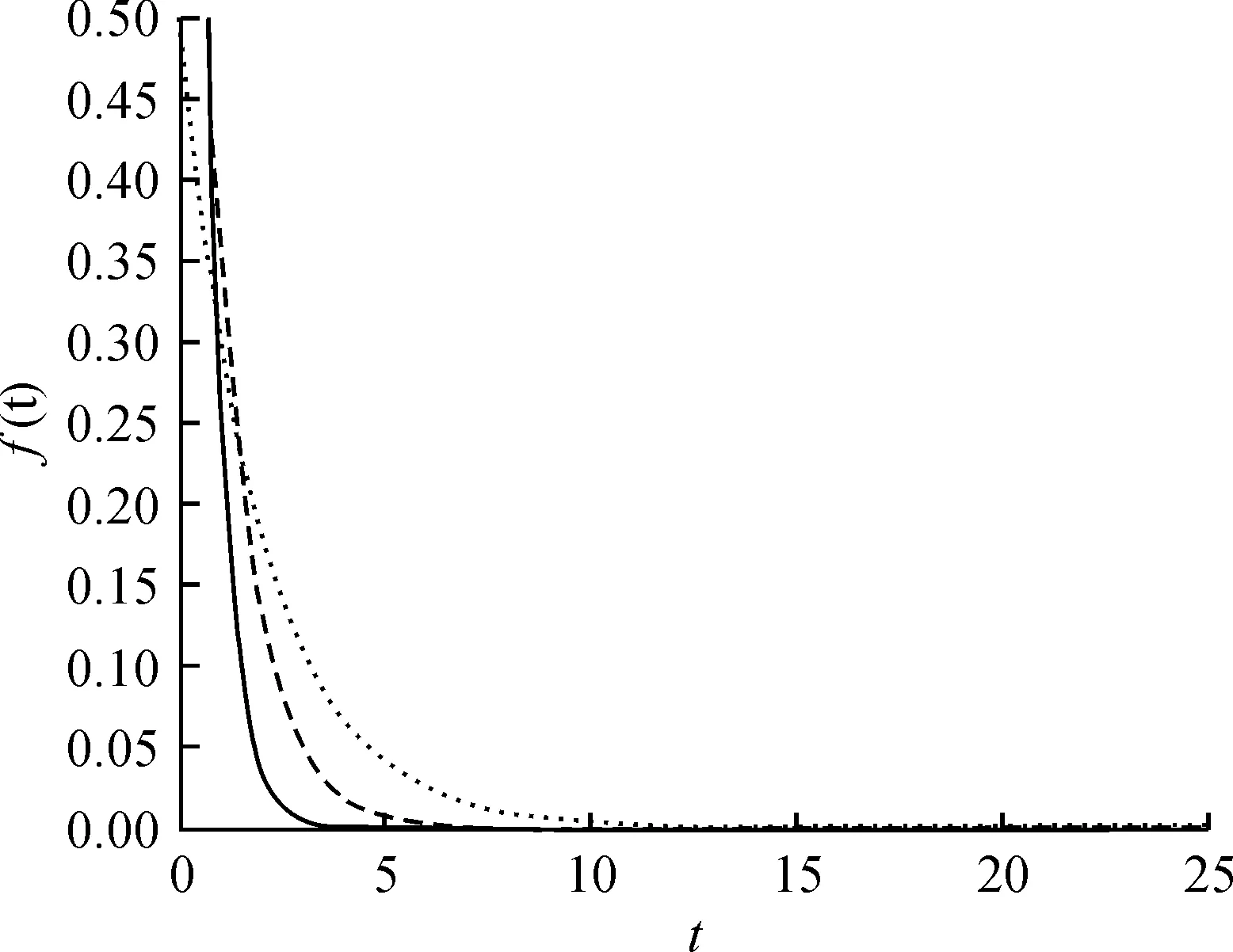
考虑到一些实证研究表明,实际作业时间t服从渐进的指数分布[6-7],研究作业时间服从指数分布的情况下的调度规则失效率是有实际指导意义的.
本文在作业时间服从指数分布的情况下分别对2项任务、3项任务的情况给出失效率的解析解;进一步,对任意多项工作的情况提出了失效率近似解的模型,并分析其有效性和失效率的敏感性.
1 2项作业的调度规则失效率计算
由上述分析,不妨假设作业i的时间Xi服从参数为1/λi的指数分布,其中λi的含义为作业i(i=1,2)完成时间的均值,
(1)
假设作业1与作业2的完成是相互独立的,且满足λ1<λ2.根据SPT规则,先安排作业1,再安排作业2.有可能出现2种情况:如图1(a)情况下,由于两作业间的工序时间期望值相差甚远,所以工序时间波动几乎不影响调度规则的有效性:当两作业的工序时间期望值接近时,由图1(b)可见,调度规则发生失效即X2>X1的可能性是不能忽略的.其中,实线表示作业2,虚线表示作业1.

图1 两项作业的工序时间分布图Figure 1 Distributed relationship processing time for two adjacent jobs
下面分析2个作业情况下的失效率:P(X1>X2)=1-P(X1 (2) 因此,2项任务时,失效率为: (3) 进一步考虑3项作业的情况下SPT规则的失效率,假设作业i时间服从参数为λi的指数分布,其中λi的含义为作业i(i=1,2,3)完成时间的均值.图2为三任务的工序时间分布图,其中:实线表示作业1,虚线表示作业2,点线表示作业3. 下面分析3项任务调度的规则失效率: P((X1>X2)∪(X2>X3)∪(X1>X3))= 1-P(X1 其中, (4) 图2 3项作业的工序时间分布图Figure 2 Distribution relationship of processing time of three jobs 因此,失效率为: 1-P(x1 (5) 假设当λ1=18,λ2=25,λ3=30时,由式(2)、(5)计算得到,前2个作业时的失效率为0.454 5;3个作业时的失效率为0.767 0. 当分析2项工作、3项工作的时候,通过对二重积分、三重积分的计算可求得解析解.对于m项任务的分析,直接求解解析解,分析较复杂,可以采用产生随机数的方式模拟得出近似结果. 假设m为作业的数量,n为模拟的迭代次数,变量sum用于累计规则失效次数,如下为随机数模拟的伪代码: sum=0 fori=1:n 产生m个服从参数为λi的指数分布的随机数Xi if (规则失效) sum=sum+1; end end 由于每一次模拟的结果是一个0-1分布,重复做n次模拟是一个n重伯努利实验. 其中: 又,当n>45时,tα/2(n-1)≈zα/2,其中,zα/2为标准正态分布的α/2分位数.所以,p的置信度为1-α的置信区间为: 通过模拟次数n的选取,控制置信区间的长度小于等于ε,由上可知,置信区间的长度为: 当λ1=18,λ2=25,λ3=30,迭代次数取值40 000时,考虑前2个作业时的失效率p的无偏估计为0.456;置信水平为1-α=0.95,区间长度小于等于ε(=0.01)的置信区间为[0.451,0.461]. 对于这3个作业的失效率的无偏估计为0.768;置信水平为1-α=0.95,区间长度小于等于ε(=0.01)的置信区间为[0.764,0.772]. 由前面所证,当2个作业时,失效率的真值为0.454 5;3个作业时失效率的真值为0.767 0.在概率意义的误差范围内与解析解是一致的,说明了本模拟求解方法的有效性. 对于多任务的情况,对于作业期望值分别为λ1=18,λ2=25,λ3=30,λ4=50的情况下,通过模拟得到4个作业的失效率为0.899;又考虑当λ1=18,λ2=25,λ3=30,λ4=42,λ5=50时,此5个作业的失效率高达0.975.当其他条件不变,任务数增多时,失效率增大,不可忽略作业时间波动的影响. 根据上述推导,失效率为λ1/(λ1+λ2),可知,失效率值取决于λ1/λ2取值,记z1=λ1/λ2,失效率为z2=λ1/(λ1+λ2),作出图3(其中,考虑到0<λ1<λ2的假设前提条件,因此λ1/λ2取值范围为(0,1)). 可见,当2个作业的期望完成时间均值的比值越接近1,则失效率越高. 图3 2个作业时失效率与作业时间期望比值的关系图Figure 3 Relationship between failure probability and processing time expectations’ ratio for two jobs (6) 可见,3个作业时的失效率取决于3个参数的比值λ1∶λ2∶λ3. 图4为3个作业时,失效率与参数比值之间的关系,考虑到0<λ1<λ2<λ3的假设,z1和z2的取值范围为(0,1).由图4可见,当3个作业的期望完成时间均值的两两比值越接近1,作业的失效率越高. 图4 3个作业时失效率与作业时间期望比值的关系图Figure 4 Relationship between failure probability and processing time expectations’ ratio for three jobs 本文还分析了失效率的敏感性,当作业时间服从指数分布的情况下,工作时间期望值的比值越接近1,失效率越大.当有多项任务时,失效率也大为增加,不能忽略作业时间波动造成的规则失效的影响.因此,为保证调度效果,当作业时间期望值较接近时,作业数较多时,应采用第二调度规则等方式来缓解单一调度规则所造成的失效率过高的问题. 参考文献: [1] 张毕西,刘永清.随机型作业计划动态排序方法研究[J].华南理工大学学报:自然科学版,2000,28(1):122-129. ZHANG Bixi,LIU Yongqing.Dynamic scheduling of stochastic operation schemes[J]. Journal of South China University of Technology:Natural Science Edition, 2000,28(1):122-129. [2] 张毕西,刘永清.静态非流水型作业排序方法研究[J].华南理工大学学报:自然科学版,1998,26(12):65-70. ZHANG Bixi,LIU Yongqing.A method for staticn·m/RND/T[J]. Journal of South China University of Technology:Natural Science Edition, 1998,26(12):65-70. [3] 张毕西.作业时间随机性及其影响分析[J].系统工程与电子技术,2002,24(2):31-33. ZHANG Bixi. Analysis of randomicity of operation time and its effect[J]. Systems Engineering and Electronics,2002,24(2):31-33. [4] CHANG Feng-Chang R. A study of factors affecting Due-Date predictability in a simulated dynamic job shop[J]. Journal of Management Science, 1994,13(6):393-400. [5] GRIFFIN Thomas E. On departure from estimated processing times[D]. Ft Lauderdale, FL: School of Business and Entrepreneurship NOVA Southeastern University, 1998: 10-48. [6] GRAVES S C,RINNOOY KAN A H G, ZIPKIN P H. Logistics of production and inventory[M]. North-Holland: Elsevier BV,1993:287-321. [7] LAW A M,KELTON W D. Simulation modeling and analysis[M].2nd ed.New York: McGraw-Hill, 1991.2 3项作业调度的规则失效率计算

3 多项作业调度的规则失效率计算模型分析
3.1 随机数模拟模型的提出

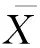
3.2 多项工作失效率的无偏估计

3.3 多项工作失效率的区间估计
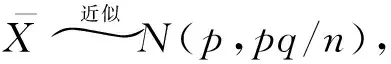

3.4 模拟次数n的选取
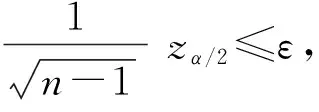
3.5 多项工作失效率模拟效果的分析
4 调度规则失效率敏感性分析
4.1 2个作业时的敏感性分析
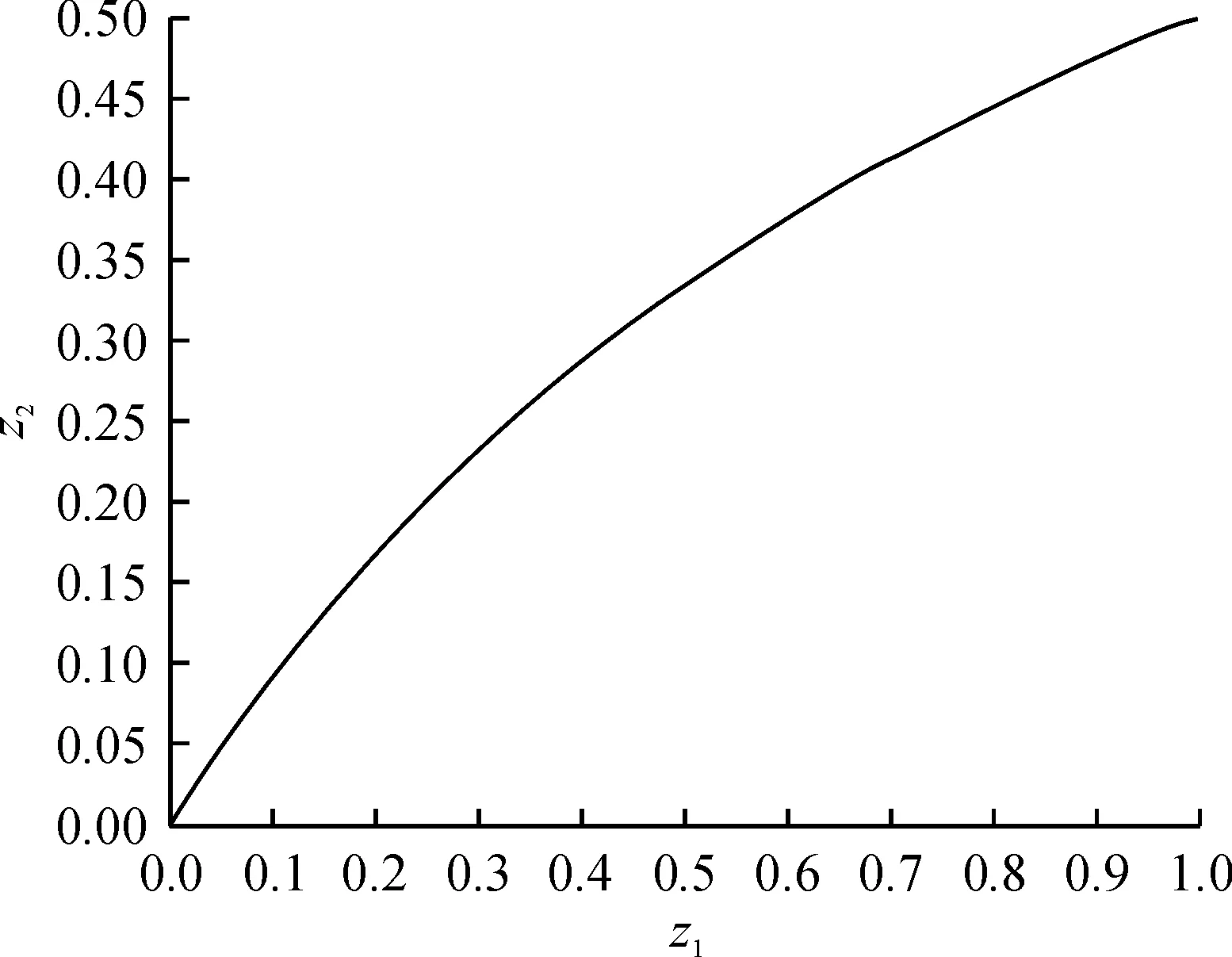
4.2 3个作业时的敏感性分析

5 结论