无环的本原反对称带号有向图的局部基与基指数

易叔勇， 尤利华

(华南师范大学数学科学学院，广东广州 510631)

称有向图D是本原的,如果存在正整数k使得对于D中任意2点vi和vj(允许i=j),在D中都有从点vi到点vj的长为k的有向途径.这样的最小正整数k称为D的本原指数,记为exp(D).有向图D是本原的,当且仅当D是强连通的,且其所有有向圈长的最大公约数为1.

设W1与W2是带号有向图S中的2条有向途径，如果W1与W2有相同的起点、相同的终点、相同的长度,并且有不同的符号,则称W1与W2是一个SSSD途径对.如果S中不包含SSSD途径对,则称带号有向图S是可幂的,否则称S是不可幂的.

令V(S)={1,2,…,n},则S的顶点经过适当地重新标号可以满足lS(1)≤lS(2)≤…≤lS(n).此时称lS(k)是S的第k个局部基.显然l(S)=lS(n).

本文涉及的其他的一些概念与记号可参阅文献[1]-[3].

文献[4]研究了n阶本原不可幂对称带号有向图S,证明了l(S)≤2n;文献[5]研究了n阶本原不可幂带号有向图的局部基的上界及极图;文献[6]研究了n阶带环的本原反对称带号有向图的局部基,证明了lS(k)≤n+k.在本文中，我们研究了n阶无环的本原反对称带号有向图S的局部基lS(k),得到了lS(k)≤max{n+l-1,n+k-1}(这里l为S中最小奇圈的长),给出了k≥l时lS(k)=n+k-1的一个极图,进而证明了n阶无环的本原反对称带号有向图S的基指数l(S)≤2n-1,给出了达到上界的极图.

1 预备知识

关于本原不可幂带号有向图,文献[3]给出了一个重要的刻画.

定理1[3]设S是一个本原带号有向图,则S是不可幂的当且仅当S中有长度为p1,p2的圈C1,C2,满足以下两情形之一:

(A1)p1是奇数,p2是偶数,sgnC2=-1;

(A2)p1和p2都是奇数,并且sgnC1=-sgnC2.称满足条件(A1)或者(A2)的一对圈C1,C2为违规圈对[3].容易验证,如果C1,C2是长度分别是p1,p2的违规圈对,则闭途径W1=p2C1(走长为p1的圈p2次)和W2=p1C2有相同的长度p1p2和不同的符号.

设S是一个本原反对称的带号有向图,则由定理1易知S是不可幂的.

引理2[5]设S是一个n阶本原不可幂带号有向图,则lS(k)≤lS(k-1)+1 (2≤k≤n).

2 主要结果与证明

设D为有向图,W是D中一条途径,记QW(x→y)为W上从x到y的最短路,l(W)表示途径W的长度.

设n为奇数,定义D1=(V,E),其中V={1,2,…,n},E={(i,i+1),(i+1,i),1≤i≤n-1}∪{(n,1),(1,n)},则易证D1是n阶本原有向图.

证明易证从点u到点u不存在长为n-2的途径,所以expD1(u)≥n-1.

下证expD1(u)≤n-1.由D1的强连通性及对称性可知,只需证明从点1到任何点i(1≤i≤n)都有长为n-1的途径即可.

再证点1到任何点i(2≤i≤n)都有长为n-1的途径.取

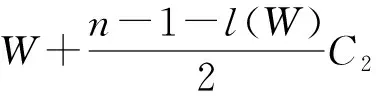
综上，expD1(u)=n-1.

证明按l的取值分如下2种情形讨论.

情形1:当l=1时.此时点u是环点,故点u到任何一点都有长为n-1的途径,进而有长大于n-1的途径,故有expS(u)≤n-1.

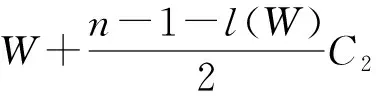
从而W是点u到点v的长为n-1的途径.

综合情形1和情形2可知expS(u)≤n-1,证毕.

定理2 设S是一个n阶无环的本原反对称带号有向图,l是S中最小奇圈的长,则对任意的k(1≤k≤n),有lS(k)≤max{n+l-1,n+k-1}.

显然,当1≤k≤l时,lS(k)≤n+l-1.

当k>l时,由引理2知

lS(k)≤lS(l)+(k-l)≤n+l-1+k-l=n+k-1.

故

结论得证.

由l(S)=lS(n)及定理2易知下面结论成立.

定理3 设S是n阶无环的本原反对称带号有向图,则l(S)≤2n-1.

下面将说明定理2和定理3中的上界是可达的.设d(u,v)表示在有向图点u到点v的距离.为此，先证明下面的引理.

引理5 设S是本原不可幂带号有向图,W1和W2是点u到点u的长为r的SSSD途径对,v是S中任意的一点,则lS(v)≤d(v,u)+r+expS(u).

设l(≥3)为奇数,定义Dn,l=(V,E),其中V={v1,v2,…,vn},E={(vi,vi+1),(vi+1,vi),1≤i≤n-1,且i≠l}∪{(v1,vl),(vl,v1)}∪{(v1,vl+1),(vl+1,v1)}.显见,Dn,l是n阶无环的本原对称带号有向图.

定理4 设l(≥3)为奇数,n≥(3l-1)/2,S=Sn,l是以Dn,l为基础有向图的n阶无环的本原反对称带号有向图,则

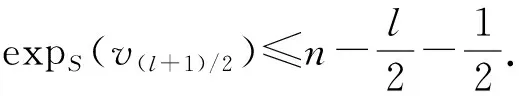
由S是反对称的可知，点v(l+1)/2到点v(l+1)/2有长为l的SSSD途径对.下面分3种情形来讨论.

情形1：当1≤i≤(l+1)/2时.由引理5可知

lS(vi)≤d(vi,v(l+1)/2)+r+expS(v(l+1)/2)≤

下面证明从点vi到点vn不存在长为n+l-i-1的SSSD途径对.

注意到点vi到点vn恰有2条路，即Q1=vivi-1…v2v1vl+1…vn,Q2=vivi+1…vlv1vl+1…vn,则l(Q1)=n-l+i-1,l(Q2)=n-i+1.设Wj(j=1,2)是点vi到点vn的长为n+l-i-1的SSSD途径对,则Wj(j=1,2)由点vi到点vn的路Rj、若干个长为l的圈Cl和若干个长为2的圈C2之并,故可设l(Wj)=l(Rj)+ajl+2bj,aj≥0,bj≥0,j=1,2.

子情形1.1：若R1=R2=Q1.此时

n+l-i-1=n-l+i-1+ajl+2bj,aj≥0,bj≥0 (j=1,2)

得(2-aj)l=2(bj+i),从而0≤aj<2 (j=1,2).若aj=1,则得到奇数=偶数的矛盾；若aj=0,则a1=a2,b1=b2,进而W1=W2,sgnW1=sgnW2.矛盾.

子情形1.2：若R1=R2=Q2.此时易得(1-aj)l=2(bj+1) (j=1,2),显然aj<1,即aj=0，从而得到奇数=偶数的矛盾.

子情形1.3：若R1≠R2,不妨设R1=Q1,R2=Q2.类似子情形1.2得到矛盾.

综上可得点vi到点vn不存在长为n+l-i-1的SSSD途径对,故当1≤i≤(l+1)/2时,lS(vi)=n+l-i.

情形2：当(l+3)/2≤i≤l时.由对称性易知lS(vi)=lS(vl+2-i)((l+3)/2≤i≤l),从而由情形1可立得lS(vi)的值.

情形3：当l

lS(vi)≤d(vi,v(l+1)/2)+r+expS(v(l+1)/2)≤

类似情形1，可证从点vi到点vn不存在长为n+i-2的SSSD途径对.故当l

由上面的讨论可知，点v(l+1)/2和点v(l+3)/2对应最小的局部基指数lS(1),点v(l-1)/2和点v(l+5)/2对应次小的局部基指数lS(2),依此类推,……,故可以直接写出第k个局部基的表达式,即

显然,定理4说明了当k≥l时,定理2中的上界是可达的.又注意到当取k=n时l(S)=2n-1,故图Sn,l也是定理3中达到上界的一个极图.

我们注意到文献[6]研究了n阶带环的本原反对称带号有向图的局部基,证明了lS(k)≤n+k,即

定理5[6]设S是n阶带环的本原反对称带号有向图,则有lS(k)≤n+k.

由l(S)=lS(n)及定理5易知有下面的结论成立.

推论1 设S是n阶带环的本原反对称带号有向图,则有l(S)≤2n.

易见,推论1中的上界也是可达的.取S2=(V,E),V={1,2,…,n},E={(i,i+1),(i+1,i),1≤i≤n-1}∪{(n,n)},且对任意的i(1≤i≤n-1),sgn(i,i+1)=+1,sgn(i+1,i)=-1,sgn(n,n)=+1.显见,S2是n阶带环的本原反对称带号有向图,由于点1到点1没有长为2n-1的SSSD途径对，所以l(S2)=2n.

由定理3和推论1,易得

推论2 设S是n阶本原反对称带号有向图,则有l(S)≤2n.

容易看到,推论2中的最大值和次大值都是可达的.

参考文献：

[1] BRUALDI R A,RYSER H J. Combinatorical matrix theory[M].Combridge: Combridge Univ Press, 1991: 53-87.

[2] BONDY J A,MURTY U S R. Graph theory with application[M]. London: Macmillan, 1976.

[3] YOU Lihua, SHAO Jiayu, SHAN Haiying. Bounds on the bases of irreducible generalized sign pattern matrices[J]. Linear Algebra Appl, 2007,427: 285-300.

[4] CHENG Bo, LOU Bolian.The bases sets of primitive zero-symmetric sign parrern matrices[J].Linear Algebra Appl, 2008, 428: 715-731.

[5] WANG Longqin, MIAO Zhengke, YAN Chao. Local bases of primitive non-powerful signed digraphs[J].Discrete Math, 2009, 309: 748-754.

[6] 范亚东,苗正科,王庆玲. 带环的本原不可幂反对称带号有向图的局部基[J]. 徐州师范大学学报:自然科学版，2009,27(3)：10-13.

FAN Yadong,MIAO Zhengke,WANG Qingling.Local bases of primitive non-powerful anti-symmetric signed digraphs with loops[J].Journal of Xuzhou Normal University:Natural Science Edition,2009,27(3)：10-13.