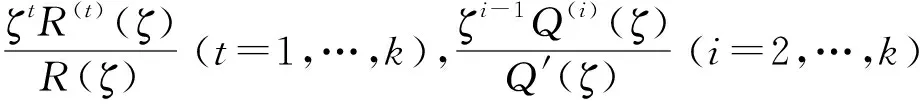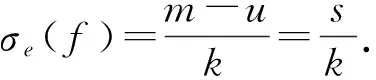一类高阶周期系数线性微分方程解的性质
陈创鑫, 陈宗煊
(华南师范大学数学科学学院,广东广州 510631)
1 引言与结果
本文使用值分布理论的标准记号[1-2].用记号σ(f)表示亚纯函数f(z)的增长级,λ(f)表示f(z)的零点收敛指数,并引进下列定义.

为了研究周期系数线性方程解的性质,BANK和LANGLEY在文献[4]中初步涉及了一个e-型级概念,CHIANG和GAO在文献[5]中比较确切地提出了e-型级的概念,即
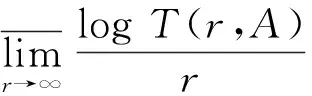
文献[5]还证明了:假设A(z)=G(ez)=G(ζ),ζ=ez,G(ζ)在0<|ζ|<+∞内解析,那么
若A(z)为周期整函数,且A(z)=B(ez)=B(ζ),ζ=ez,B(ζ)为ζ的有理函数.明显地必有下列形式B(ζ)=ζ-m(anζn+an-1ζn-1+…+a0).明显地,若n>m,则ζ=∞必是B(ζ)的n-m阶极点.
已有多人对二阶周期系数方程解进行了研究[4-5,7-9],而对高阶周期系数方程解的研究甚少.BANK和LANGLEY在文献[4]中得到了下面的重要结果.
定理1 假设k≥2,A0是以2πi为周期的整函数,假设A0是ez的有理函数,A1,…,Ak-2为常数.如果f(z)(≢0)是微分方程
f(k)+Ak-2(z)f(k-2)+…+A0(z)f=0
(1)
的解且满足
(2)
那么存在q(1≤q≤k)满足f(z)和f(z+q2πi)线性相关.
定理2 假设k≥2,A0是以2πi为周期的整函数,假设A0是ez的有理函数,A1,…,Ak-2为常数.如果f(z)(≢0)是微分方程(1)的解且满足式(2),那么存在整数q(1≤q≤k),常数d,及在1<|ζ|<+∞内解析的有理函数R(ζ)和S(ζ),使得
定理1指出存在q(1≤q≤k),满足f(z)和f(z+q2πi)线性相关.后来,陈宗煊[6]证明了定理3,指出B(ζ)是多项式且其次数n不能被k整除时,f(z)和f(z+2πi)是线性无关的.
定理3 假设k≥2,A0是以2πi为周期的整函数,假设A0=B(ez)=B(ζ),ζ=ez,B(ζ)是n次多项式,且n不能被k整除;A1,…,Ak-2为常数.如果f(z)(≢0)是微分方程(1)的解且满足式(2),那么f(z)和f(z+2πi)线性无关,且有σ2(f)=1和σe(f)=n/k.
命题1 假设f(z)为亚纯函数,那么
(i)如果σ2(f)<1,则σe(f)=0;
(ii)如果σ2(f)>1,则σe(f)=∞;
(iii)如果0<σe(f)<∞,则σ2(f)=1.
一个自然的问题是,当B(ζ)(ζ=ex)是有理函数时,f(z)和f(z+2πi)的线性相关性将如何?本文在下面的定理4中回答了这个问题.
定理4 假设k≥2,A0是以2πi为周期的整函数,假设A0(z)=B(ez)=B(ζ),ζ=ez,B(ζ)=ζ-m×(anζn+…+a0),不退化为常数,其中an≠0,且ai(i=0,1,…,n)为常数.A1,…,Ak-2为常数.设u=min{i:ai≠0,i=0,1,…,n},并令s=max{n-m,m-u}.如果f(z)(≢0)是微分方程(1)的解且满足式(2),那么成立σ2(f)=1及σe(f)=s/k.
定理5 假设k≥2,A0是以2πi为周期的整函数,假设A0=B(ez)=B(ζ),ζ=ez,B(ζ)=ζ-m(anζn+…+a0),不退化为常数.其中an≠0,且ai(i=0,…,n)为常数.A1,…,Ak-2为常数.设u=min{i:ai≠0,i=0,1,…,n},令s=max{n-m,m-u}.如果f(z)(≢0)是微分方程(1)的解并满足式(2),且条件(i)或(ii)成立:
(i)当n>m时,n-m不能被k整除;
(ii)当n≤m时,m-u不能被k整除.
那么f(z)和f(z+2πi)线性无关,并且成立σ2(f)=1及σe(f)=s/k.
2 证明所需引理
引理1[10]假设F(z)除了在∞点有孤立本性奇点外,在R0<|z|<∞内解析,那么F(z)可以表示成F(z)=zmΦ(1/z)P(z)eh(z),其中m为整数,P(z)是由F(z)的零点形成的多项式或Weierstrassion乘积,h(z)为整函数,Φ(1/z)在R0<|z|≤∞内(含∞点)解析且Φ(1/z)|z=∞=1,确切地Φ(1/z)=eΦ1(1/z),Φ1(1/z)在R0<|z|≤∞内(含∞点)解析且Φ1(1/z)|z=∞=0.


引理3[6]假设g(ξ)除了在∞点有孤立本性奇点外,在R0<|z|<∞内解析,那么
(i)g(ξ)可以表示成g(ξ)=ξmψ(ξ)F(ξ),其中m为整数,F(ξ)为整函数,ψ(ξ)在R0<|z|≤∞内(含∞点)解析,且ψ(ξ)≠0,ψ(∞)=1,当ξ→∞时
(3)

(4)
其中ν(ρ)为整函数F(ξ)的中心指标;
(iii)g(ξ)可以表示成
g(ξ)=ξmW(ξ)eh(ξ),
(5)

如果g(ξ)仅有有限多个零点,那么当ξ→∞时
注1 关于区域0<|ξ|<∞内的Nevanlinna特征函数.假设G(ξ)在0<|ξ|<∞内亚纯,考虑当ξ→∞时,G(ξ)的增长性,可以由|ξ|≥1内的Nevanlinna理论[12]来考虑,定义
(6)
和N1(ρ,G)为|ξ|≥1内的极点的计数函数,以及
T1(ρ,G)=m1(ρ,G)+N1(ρ,G).
(7)
由文献[7]可知:对于m1(ρ,G),与Tumura-Clunie引理相应的结果仍然成立,以及G(ξ)在ξ=∞有极点的充分必要条件为T1(ρ,G)=O(logρ).
考虑当|ξ|=ρ→ 0时,G(ξ)的增长性,可以定义G*(ξ)=G(1/ξ),由考虑当ρ→∞时,T1(ρ,G*)的增长性来决定ρ→ 0时,G(ξ)的增长性.
我们还可定义G(ξ)在点ξ=∞的增长级[7]为
(8)
而G(ξ)在点ξ=0的增长级定义为
σ0(G)=σ∞(G*).
(9)
另一方面,如果G(ξ)在0<|ξ|<∞内解析,则N1(ρ,G)=0.由引理1和引理3可知G(ξ)可表为
G(ξ)=ξnψ(ξ)F(ξ),
(10)
其中n为整数,ψ(ξ)在1<|ξ|≤∞内解析,ψ(ξ)≠0,ψ(∞)=1,F(ξ)为复平面内的整函数.由式(6)、(7)和(10)可知当|ξ|=ρ充分大时
m1(ρ,G)=m(ρ,F)+O(logρ),
T1(ρ,G)=T(ρ,F)+O(logρ),
结合式(8),得到
(11)
考虑当|ξ|→∞时,G(ξ)的增长性,我们还可记
M1(ρ,G)={|G(ξ)|:|ξ|=ρ(>1)}.
(12)
由于ψ(ξ)≠0,ψ(∞)=1,由式(10)、(12),可知当ρ充分大时
(13)
由于ψ(ξ)≠0,ψ(∞)=1,由式(11)、(13),可知
(14)
引理4[6]假设整函数f(z)满足f(z)=ξdG(ξ),其中d为常数,ξ=ez/q,q为正整数,G(ξ)在0<|ξ|≤∞内解析,那么
(15)

(16)
3 定理4的证明

M[T(r,f)]k+1,
(17)
其中M(>0)为常数.
下面根据n与m的大小关系来证明σ2(f)=1及σe(f)=s/k.

首先,若u |A0(z)|=M(r,A0)=|an|e(n-m)r(1+o(1)), 其中an≠0,au≠0为常数.将其代入式(17),并注意到s≥1,n-m≥1,可得σ2(f)≥1.另一方面,由Wiman-Valiron理论[13],从方程(1)可得σ2(f)≤1,故σ2(f)=1. 首先考虑σ∞(G).由引理3的(i),G(ξ)=ξd×ψ(ξ)F(ξ),其中m为整数,F(ξ)为整函数.ψ(ξ)在1<|ξ|≤∞(含∞点)内解析且ψ(ξ)≠0,ψ(∞)=1. 将f(z)=ξdG(ξ)代入方程(1),得到 (18) (19) 其中ν(ρ)为整函数F(ξ)的中心指标.由于F(ξ)为超越整函数,由式(18)、(19)得到 (1+o(1))+qkanξq(n-m)(1+o(1))=0, (20) 再由式(14)可知 (21) 下面考虑σ0(G).由式(9),σ0(G)=σ∞(G*),其中G*(t)=G(1/t),ξ=1/t.由归纳法,可得 G(s)(ξ)=(-1)s(G*)(s)(t)ts+s+ (22) 其中dj为常数.由条件可假设B(ξq)=(ξ-mq)×(anξnq+…+a0),其中an(≠0),…,a0为常数,且n>m,再结合u的定义,可知 (23) 将式(22)、(23)代入式(18),得到 (24) G*(t)=tm*ψ*(t)F*(t), (1+o(1))+(-1)kqk[ant(m-n)q+…+ aut(m-u)q]=0, (25) 其中ν*(ρ)为整函数F*(t)的中心指标. 下面再根据u与m的大小关系进行讨论. 若u (1+o(1))+(-1)kqkaut(m-u)q(1+o(1))=0, (26) 再由式(14)可知 若u≥m,则由式(25)得 (1+o(1))+O(1)=0, (27) 下面考虑情形(ii):当n A0(z)=anζn-m+an-1ζn-1-m+…+a0ζ-m= anζn-m+an-1ζn-1-m+…+auζu-m, 而u-m 首先考虑σ∞(G).由式(18)、(19)知 (1+o(1))+O(1)=0, (28) 其中ν(ρ),Cj,ρ如式(18)~(20)所述.如果F(ξ)为超越整函数,那么ν(ρ)→∞,则式(28)矛盾.从而F*(ξ)最多为多项式,因此σ(F)=0.由式(14)可知 σ∞(G)=σ(F)=0. (29) 下面考虑σ0(G).由式(24)可得 o(1))+(-1)kqk[ant(m-n)q+…+aut(m-u)q]=0, (30) 由于m-u>m-n>0,故由式(30)可得 (1+o(1))+(-1)kqkaut(m-u)q(1+o(1))=0, (31) A0(z)=B(ζ)=am+am-1ζ-1+…+a0ζ-m= am+am-1ζ-1+…+auζu-m, (32) 而B(ζ)不为常数,故u 首先考虑σ∞(G).因为A0(z)=am+am-1ζ-1+…+auζu-m,类似于情形(ii)可得σ∞(G)=0. 再考虑σ0(G).由式(17)、(22)可知 (1+o(1))+(-1)kqk[am+am-1tq+…+ aut(m-u)q]=0, (33) 从而可得 (1+o(1))+(-1)kqkaut(m-u)q(1+o(1))=0, (34) 先证明在条件(i)下定理成立. 假设f(z)(≢0)是微分方程(1)的解且满足式(2).如果f(z)与f(z+2πi)线性相关,由f(z)满足式(2),那么由定理1及定理2,可知f(z)在1<|ζ|<∞内可表为 f(z)=R(ez)exp(dz+Q(ez))= edzR(ez)exp(Q(ez))=ζdR(ζ)exp(Q(ζ)), (35) 其中d为整数,ζ=ez,R(ζ)和Q(ζ)皆为ζ的有理式,且在1<|ζ|≤∞内解析.将式(35)代入方程(1)得到 (36) (37) 由于Q(ζ)为有理式,故当|ζ|→∞时,有 (38) 由式(37)、(38)可知 |Fj(ζ)|=O(1) (j=0,…,k-1). (39) 倘若ζ=∞为Q(ζ)的解析点,则当|ζ|→∞时,|ζQ′(ζ)|=O(1),而n>m,故ζ=∞为B(ζ)的n-m阶极点,因而式(36)不可能成立.从而ζ=∞不可能是Q(ζ)的解析点.因此不妨设ζ=∞为Q(ζ)的α阶极点,由式(36)、(39)及ζ=∞为B(ζ)的n-m阶极点,得到kα=n-m,这与假设条件:n-m不能被k整除相矛盾,从而f(z)和f(z+2πi)线性无关. 结合定理4,可以得到 再证明在条件(ii)下定理也成立. 令B*(t)=B(1/t)=B(ζ),由于n≤m,故 B*(t)=antm-n+an-1tm+1-n+…+autm-u(au≠0). 假设f(z)(≢0)是微分方程(1)的解且满足式(2).如果f(z)与f(z+2πi)线性相关,由于f(z)满足式(2),那么由定理1及定理2,可知f(z)在1<|t|≤∞内可表为 f(z)=td1R*(t)exp(Q*(t)), (40) 其中d1为整数,t=e-z,R*(t)和Q*(t)在1<|t|≤∞内解析.将式(40)代入方程(1)得 参考文献: [1] 杨乐. 值分布论及其新研究[M]. 北京: 科学出版社,1982. [2] HAYMAN W K.Meromorphic function[M]. Oxford: Clarendon Press,1964. [3] 仪洪勋,杨重骏. 亚纯函数唯一性理论[M]. 北京: 科学出版社,1995. [4] BANK S B, LANGLEY J K. Osillation theorems for higher order linear differential equations with entire periodic coefficients[J]. Comment Math Univ St Paul, 1992,41:65-85. [5] CHIANG Y M, GAO S A. On a problem in complex osillation theory of periodic second order linear differential equations and some related perturbation results[J]. Ann Acad Sci Fen Math,2002,27:273-290. [6] 陈宗煊. 一类高阶周期系数线性微分方程解的性质[J]. 数学学报, 2006,49(5):989-998. CHEN Zongxuan. A property of solutions for a class of higher order periodic linear differential equations[J].Acta Mathematica Sinica,2006,49(5):989-998. [7] BANK S B, LAINE I. Representations of solutions of periodic second order linear differential equations[J]. J Reine Angew Math, 1983,344:1-21. [8] GAO S A. A further result on the complex oscillation theory of periodic second order linear differential equations[J]. Proc of Edinburgh Math Soc, 1990, 33: 143-158. [9] GAO S A. A property of solutions and the complex oscillation for a class of higher order periodic linear differential equations[J]. Acta Mathematical Applicatac Sinica, 2002,25:642-649. [10] VALIRON G. Lectures on the general theory of integral functions[M]. New York: Chelsea, 1949. [11] GUNDERSEN G. Estimates for the logarithmic derivative of a meromorphic function, plus similar estimates[J]. J London Math Soc, 1988,37(2):88-104. [12] BIEBERBACH L. Theorie der gewohnlichen differentialgleichungen[M]. Berlin,Heidelberg,New York: Spinger-Verlag,1965. [13] 何育赞,萧修治. 代数体函数与常微分方程[M]. 北京:科学出版社,1988. [14] INCE E. Ordinary differential equations[M]. New York: Spinger-Verlag,1927.
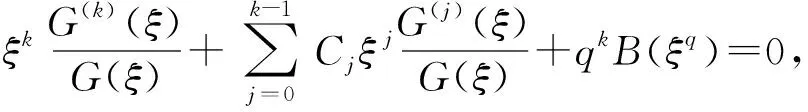




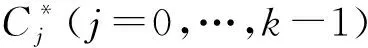

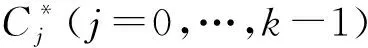


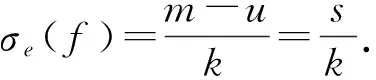

4 定理5的证明