交会对接气浮仿真平台视觉辅助姿态确定

魏喜庆 宋申民

（哈尔滨工业大学控制理论与制导技术研究中心，哈尔滨150001）

1 引言

航天器交会对接（Rendezvous and Docking，RVD）过程中，要求两个航天器不能发生碰撞，这是至关重要的安全要求。为了满足RVD的高精度和苛刻安全要求，需要大量理论研究和物理仿真。利用气浮技术进行全物理仿真，是发展较早且广泛采用的一种有效手段［1］。四自由度对接仿真平台采用了单轴气浮轴承的形式，开发对接与分离的地面演示系统，用于仿真验证最后逼近阶段的制导与控制规律、卫星姿态控制以及位姿测量系统的有效性和可靠性。

位姿估计是计算机视觉的一个重要内容，n点透视（Perspective-n-Point，PnP）问题具有常规的解法［2］，但是快速准确的求解此类问题，仍一直是学者努力的方向。Nister给出了求解位姿的五点算法［3］，Lu基于n点透视提出了一种正交迭代方法求解位姿［4］。利用陀螺仪以及星敏感器等装置的扩展卡尔曼滤波（EKF）姿态确定算法，在20世纪80年代初成为研究热点［5-6］，并逐渐发展为一种成熟方法，成功应用在了多种飞行器上［7］。

本文的主要研究利用视觉摄像机获得的姿态角和俯仰与偏航轴陀螺仪输出的角速度来有效地确定姿态。由于视觉系统的CCD相机的视野有限，仅有40°左右，因此一旦主动星转动使目标超出视野，就会造成视觉定姿失败；而陀螺仪输出角速度具有自主性且输出信号更新速率快，但是漂移随时间累积的特点。为了将两者优势结合起来，更好地获得主动星的姿态，本文采用了这种成熟的EKF算法，充分利用了姿态运动学方程和陀螺仪模型以及视觉的观测数据。由于EKF的初始状态协方差阵的选取对滤波精度影响较大，且本系统的协方差阵为6维方阵，如果初值选取不当会造成滤波器发散；又由于求取滤波增益时需要进行求逆运算，存在求解计算量大的问题。为了克服这些困难，本文提出了一种新的姿态估计方法，使用四元数和改进的罗德里格参数（MRPs）相结合，利用李雅普诺夫 （Lyapunov）函数推导出一种非线性观测器，并证明了观测器的全局收敛性。

2 四自由度对接仿真平台

四自由度对接仿真系统由追踪星、目标星和光滑无摩擦的大理石平台组成，用于完成对接的地面演示试验。追踪星由支撑系统和星体系统两部分组成，支撑系统的底座下面安装有平面气浮垫，通过喷气在气浮垫和大理石平台之间形成一层气膜，支撑起了整个追踪星，可以实现整个系统与大理石平台的无摩擦二维平动和绕垂直轴的转动；支撑系统和星体系统由单轴气浮轴连接，既能支撑起星体，又能保证星体绕侧向轴做无摩擦的俯仰运动。因此系统可模拟空间无摩擦的四自由度运动。

星体的执行机构包括喷嘴和飞轮。仿真平台上的13个冷气喷气喷嘴，可以实现二维的平动与转动。另外采用了两个反作用飞轮，与喷气系统结合来控制星体的俯仰与偏航运动，具体的控制实现方式是采用大范围的转动机动时使用喷气驱动，而微调时用飞轮控制。

测量系统包括惯性和视觉测量系统两部分。惯性测量装置包括两个正交放置的陀螺仪，可以输出偏航和俯仰两个方向的角速度。视觉测量系统是对接系统的主要测量装置，通过目标星上安装的主动目标器，安装在追踪星上的CCD相机来获取目标器上的发光点成像，通过图像处理、特征匹配和利用投影姿态与定标迭代（Pose from Orthography and Scaling with Iterations，POSIT）算法［8］可以得到两个星体之间的相对位姿，从而为气浮追踪星提供所需的制导信息，如图1所示。

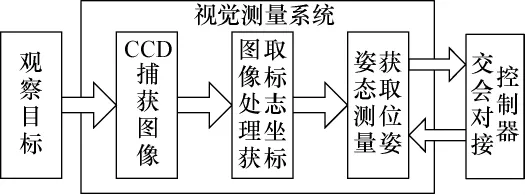
图1 视觉测量系统原理图Fig.1 Diagram of vision measurement system

3 姿态运动方程

3.1 四元数姿态运动学方程

四元数由一个三维的矢量和一个标量两部分组成，写成如下形式［9］：式中q13和q4分别是四元数矢量和标量部分；e为旋转轴；φ为绕旋转轴旋转的角度。由于四元数四维的向量来表示3个角度，因此四元数各个元素彼此并不独立，有‖q‖＝1。四元数表示的旋转矩阵［6］：

式中Ⅰ3×3为三维单位阵，［q13×］为叉乘矩阵。叉乘矩阵定义为：a×b＝ ［a×］b，其中

式中a1，a2和a3是矢量a的三个分量。

四元数乘法的采用Lefferts，Markley和Shuster等人定义［6］：

如果将式（4）中的q定义为原始四元数，q′定义为增量四元数，则四元数q″的含义是在q的基础上增加了q′，表示为姿态矩阵的形式［9］：从而可以看出，从A（q）基础上左乘A（q′）得到关于q″的姿态矩阵，与通常使用的姿态角表示的姿态矩阵连续旋转的顺序相同。

四元数的姿态运动学方程［10］为

式中ω是体系相对于惯性系的角速度在体系下的表示。

3.2 修正的罗德里格参数

修正的罗德里格参数定义为p＝q13／（1＋q4）＝etan（φ／4）

修正的罗德里格参数相对于欧拉角具有的优势是只有在360°时才会出现奇异值。另定义：

在不致发生混淆的情况下，为了叙述方便下文将ap也称为修正的罗德里格参数。从式（7）的最后一项能够看出，当φ为小角度时，φ与ap（ap的幅值）近似相等。

反之，由式（7）和‖q‖＝1也可以得到由修正罗德里格参数表示的四元数［11］：

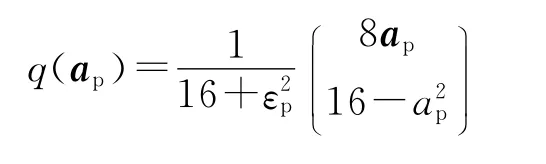
4 扩展卡尔曼滤波

4.1 状态方程

定义真实四元数表示为四元数相乘［12］：

式中qref（t）代表一个参考四元数，δq（ap（t））代表qref（t）与真实四元数q（t）之间的误差四元数。易知有修正的罗德里格参数ap（t）与δq（ap（t））互为对应。

由于qref（t）也是单位四元数，同样遵守式（6）的运动学方程

式中ωref是参考姿态的参考角速度，为简便起见，从公式（9）以后略去公式中变量关于时间的表达。

对式（8）进行求导，并将式（6）和（9）代入可得［12］：

式中 角速度ω可以由陀螺输出ωout来表示

式中b为陀螺漂移；ηv和ηu为不相关零均值白噪声，其协方差阵分别为σvⅠ3×3和σuⅠ3×3。当角度偏差δq（ap）很小时，由式（10）易知参考角速度ωref近似于估计角速度，从而参考角速度可以写为

将误差四元数写为修正的罗德里格参数形式，得ap＝4δq13／（1＋δq4），将其代入式（10）得

由公式（11）和（12）可得：

式中 Δb＝b-，将式（14）带入到式（13）并忽略关于ap的高阶项，可得

所以系统的误差状态方程可以得出

高斯白噪声w均值为零，方差阵为

4.2 测量方程

追踪星通过CCD像机观测目标星上的特征点靶标，可以测量追踪星和目标星的相对姿态，目标星固定不动，因此可以设目标星的特征点坐标系为参考坐标系。假设追踪星星体系和参考系之间的姿态角四元数测量值为qobs，观测值和姿态预测四元数的偏差为δq（aobs）：

式中aobs为与δq（aobs）相对应的修正的罗德里格参数。

因此系统状态偏差离散测量模型可以简化为

其中量测噪声v（k）的数学期望值和协方差阵分别为：

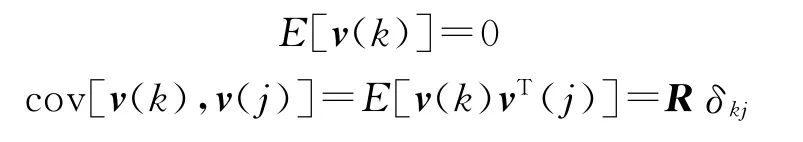
因此由式（16）可知系统的量测矩阵：

4.3 EKF姿态确定流程

由姿态确定的EKF工作流程可以看出，滤波器经过初值设置后，主要步骤是预测和更新，与普通EKF类似。但由于本文是关于偏差的EKF，所以在预测和更新之后增加了偏差量对预测值的补偿。

5 非线性观测器设计

5.1 非线性观测器

为了克服EKF存在的初值调节困难和避免滤波更新中矩阵求逆导致的计算复杂性，下文基于Lyapunov方法设计了一种新型的非线性观测器。观测器的设计过程同样利用了四元数和修正的罗德里格参数，并且充分利用了系统的姿态运动方程，证明了观测器的渐进稳定性，从而在具有较大初值的情况下保证了观测器的收敛。

定义李雅普诺夫函数：

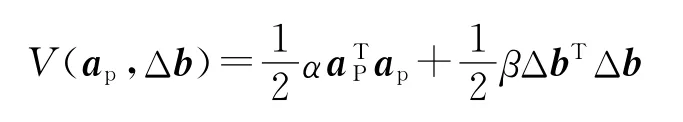
其中，α＞0，β＞0为常值系数。对V进行求导：

将式（12）中参考角速度ωref重新定义为

其中，ε为修正量，从而

将其带入式（13），忽略ap高阶项和ηv，类似于式（15）得

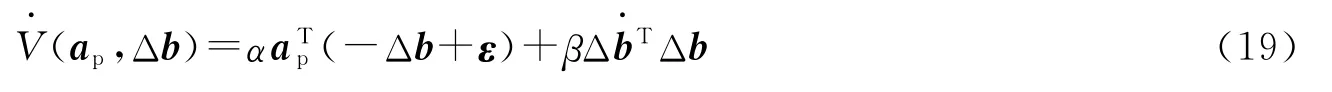
当选择：

式中λ、γ为系数，λ＞0，γ＞0，则式（19）可变为

易知（ap，Δb）是负定的，因此式（18），（20）和（21）是全局渐进稳定的。

5.2 非线性观测器流程

由非线性观测器的工作流程看出其与EKF的流程类似，但是形式相对简单。相比较矩阵运算较少，没有关于矩阵求逆的运算，易于实现，计算量也较小。

6 试验结果与分析

这部分通过四自由度对接仿真平台试验来验证扩展卡尔曼滤波器和非线性观测器的正确性和有效性。试验采用的陀螺仪的更新频率达到100Hz，采用的陀螺仪测量噪声标准差和陀螺漂移噪声标准差分别为而视觉采样周期为10Hz，采用的CCD相机由于光线变化和图像处理等原因，具有σ＝0.01°标准差的噪声影响。假设初始陀螺漂移的估计值为初始姿态四元数估计q0＝［0 0 1 0］T。设姿态角偏差的初始协方差为0.01（°）2，陀螺漂移协方差为3×10-9［（°）／s］2。

试验时间为500s，图2中by、bz分别表示俯仰和偏航方向的陀螺漂移估计误差随时间变化曲线，图3为俯仰和偏航方向姿态角估计误差随时间变化曲线。从图2、图3可看出陀螺仪漂移和姿态角估计很快收敛，但是由于CCD相机量测更新频率只能达到10Hz，估计后的姿态角精度不高，姿态角误差精度略低于0.1°。从图2中可以看到，对于陀螺漂移的估计EKF和非线性观测器的效果接近，但是对于姿态角的估计，EKF滤波过程中间偶尔出现误差较大的情况，非线性观测器估计精度要优于EKF。

图2 陀螺漂移估计误差Fig.2 Gyros bia estimate error

图3 姿态角估计误差Fig.3 Attitude estimate error

其中主要的一个因素是EKF初始协方差阵仅对角线元素就有6个参数，其选取对EKF精度有较大影响，因此选取的参数很难选到一个最优的参数，难以发挥EKF的最佳性能，导致非线性观测器性能表现优于EKF。而所用到的非线性观测器只用到了α／β，γ和λ共3个参数，调整起来相对容易。由于试验表明这3个参数对姿态角的估计影响不大，只对陀螺仪漂移估计具有较大影响。图4～图6给出了非线性观测器3个参数对估计精度影响结果（为简化只给出非线性观测器的偏航方向陀螺漂移误差随时间变化曲线）。

由图4中by和bz随时间变化的曲线分析，在其他两个参数γ和λ固定的情况下只调整α／β，by受参数变化影响较小，而bz受影响较大，随α／β增大非线性观测器陀螺漂移估计初始误差随之增加，因此α／β不宜取较大值，取α／β＝0.01即可。

由图5可知，当其他两个参数固定只改变γ，当γ取值较小时收敛较慢滤波器收敛缓慢，因此γ取10可以保证滤波器的快速收敛。

由图6可知，当其他两个参数固定只改变λ大小，发现λ值对滤波器具有较明显的影响。随着λ增大，滤波器误差会随之增大，甚至会造成不稳定的现象，因此取λ＝1即可。

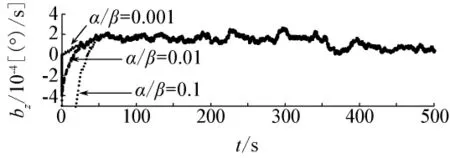
图4 α／β值对观测器估计值影响Fig.4 Effect ofα／βon the observer estimate

图5 γ值对观测器估计值影响Fig.5 Effect ofγon the observer estimate

图6 λ值对观测器估计值影响Fig.6 Effect ofλon the observer estimate

7 结束语

本文首先介绍了包含两轴陀螺仪和一个视觉测量系统的四自由度对接仿真平台的姿态确定系统。为了充分利用两种测量装置进行姿态确定，首先设计了采用四元数和MRPs结合的经典EKF算法。为了克服EKF算法的不足，本文提出了一种非线性观测器的姿态确定方法并用Lyapunov方法证明其收敛性。通过对传统EKF和新设计的非线性观测器分别进行试验对比，所设计的非线性观测器用于本系统不仅精度高于EKF算法，且具有需要调节参数少，简单易行的优势。

［1］SCHWARTZ J，PECK M，HALL C.Historical review of air-bearing spacecraft simulators［J］.Journal of Guidance，Control and Dynamics，2003，26 （4）：513-522.

［2］FISCHLER M，BOLLES R.Random sample consensus：aparadigm for model fitting with applications to image analysis and automated cartography［J］.Communications of the ACM，1981，24 （6）：381-395.

［3］NISTER D.An efficient solution to the five-point relative pose problem［C］.IEEE Computer Society Conference on Computer Vision and Pattern Recognition，Madison，WI，United states，2003.

［4］LU C P，HAGER G D，MJOLSNESS E.Fast and globally convergent pose estimation from video images［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22：610-622.

［5］MURRELL J.Precision attitude determination for multimission spacecraft［C］／／Proceedings of the AIAA Guidance，Navigation，and Control Conference，Palo，CA，United States，1978.

［6］LEFFERTS E J，MARKLEY F L，SHUSTER M D.Kalman filtering for spacecraft attitude estimation［J］.Journal of Guidance，Control，and Dynamics，1982，5（5）：417-429.

［7］ANDREWS S F，BILANOW S.Recent flight results of the TRMM Kalman filter［C］.AIAA Guidance，Navigation，and Control Conference and Exhibit，Monterey，CA，United States，2002.

［8］DEMENTHON D F，DAVIS L S.Model-based object pose in 25lines of code［J］.International Journal of Computer Vision，1995，15 （1-2）：123-141.

［9］SHUSTER M.A survey of attitude representations［J］.Journal of the Astronautical Sciences，1993，41 （4）：439-517.

［10］KIM SG，CRASSIDIS J L，CHENG Y，et al.Kalman filtering for relative spacecraft attitude and position estimation［J］.Journal of Guidance，Control，and Dynamics，2007，30（1）：133-143.

［11］CRASSIDIS J L，MARKLEY F L.Attitude estimation using modified rodrigues parameters［C］／／Proceedings of the American Astronautical Society Greenbelt，Maryland，United States，1996.

［12］MARKLEY F L.Attitude error representations for Kalman filtering［J］.Journal of Guidance，Control，and Dynamics，2003，26（2）：311-317.

［13］CRASSIDIS J，JUNKINS J.Optimal estimation of dynamic systems［M］.Boca Raton：Chapman ＆ Hall，2004：419-433.