奇点光学法诊断生物组织病理性病变
邓 凯,曾阳素,,李建龙
(1.湖南师范大学物理与信息学院,中国 长沙 410081;2.邵阳学院激光技术研究所,中国 邵阳 422100)
相干激光辐射与物体作用后,输出光源就会带有物体结构的信息.这些信息包含在光强的空间频率分布,相位和场的极化参量中.很显然,解读输出场信息的方法并不一样,这要由物体本身的性质决定.然而物体场(把输出场叫做物体场)是被测量物体的一个印记,这个印记可以从输出场的上面提到的参数的空间或角度分布反映出来.
历史上,统计场的空间结构用相关性来描述,其中相关性由电场在两个不同位置的平行成分的关联来决定[1].物体场关联的另一描述方法是基于极化状态的分析.这是由给定点场的复振幅的垂直成分最大关联值来定义的[2].实光场是以相关性和极化在空间同时改变为特征的.
众所周知,自然界的物体的结构和形成的物体场都可以分成决定的(规律的),随机的(统计的)和不规则的(自相似)这三种结构.当然,描述不同结构的参量也会大不相同.然而,Mandelbrot阐述的一个普遍原理却是正确的,该原理表明给定物体的不规则性会在描述给物体不规则性的参量中显现出来.可以设想这个原理对一切物体和结构都是成立的,包括决定的和统计的物体和结构,没有任何特别的限制.
这种技术将用于物体场极化结构的拓扑学的和统计学描述方法关联性分析的研究中.研究对象是人体的双折射组织(真皮层,肾和子宫颈),这些组织对光的极化状态的传输性都比较好.
1 生物组织图像中的极化不均匀性和奇点
众所周知,在分析物体场的极化结构时的拓扑方法中,假设了右旋的圆偏振和椭圆偏振光与左旋的圆偏振和椭圆偏振光被平面上等位线的线偏振分割开来[3].上面提到的模型使我们想到形成非均匀极化场的原理,运算法则和方案,而且明白的阐释在局域范围内形成这种结构的可能机制.这种方法是基于在电磁场中形成线性和圆偏振衰减极化奇点的方法.依赖于这些区域的尺寸,形式,分布和可重复性频率(例如s等值线),我们得到了不同尺寸的物体场独特的决定,统计和不规则的极化态分布.
在本文中,参考文献[3]的模型是分析从生物组织(BT)散射出来的场的极化结构的基础.根据该模型,这些物体可用含两个参量的不规则晶体矩阵表示.单轴晶体,双折射生物组织纤维代表极化变换矩阵,其在坐标r的特性用琼斯算符描述:
(1)
其中ρ定义为双折射纤维束进入生物组织样本平面的角度,生物组织给光场正交的E0x,E0y带来的相移为δ.根据(1)式,生物组织图像的振幅相位结构可能由下面这个矩阵等式决定:
(2)
其中[Ex(r),Ey(r)]是生物组织图像上坐标为r点处的电场的复振幅.
为简化计算但又不至于引起分析的不完全性,我们考虑入射光为线偏振光,且相对于入射面的角度为0,于是得到:
(3)
考虑到公式(3),可以将(2)式写成:
Ex(r)=E0x[cos2ρ(r)+sin2ρexp(-iδ(r))],
Ey(r)=E0x[cosρ(r)sinρ(r)[1-exp(-iδ(r))]],
(4)
为了确定生物组织图像在不同点的局域极化态,我们应使用相应的相干矩阵:
(5)
在椭圆偏振的情况中,生物组织图像中的光学各向异性区域的垂直振动的振幅表达式可能为:
Ex=cosρ(E0xcosρ+E0ysinρexp(-iδ0))+sinρ(E0xsinρ-E0ycosρexp(-iδ0))exp(-iδ),
Ey=sinρ(E0xsinρ+E0ycosρexp(-iδ0))+cosρ(E0xcosρ-E0ysinρexp(-iδ0))exp(-iδ),
(6)
根据式(5),生物组织图像上的极化方位角α(ri)和椭圆率β(ri)代表极化不均匀结构:

(7)
这里ri≡rm,n是由记录生物组织图像的CCD像素决定的坐标全体,α是方位角,β是点r的光极化椭圆曲率.
从(6)式看出,生物组织图像最可能的极化态是椭圆偏振,其椭圆曲率参数由(7)式给出.考虑到(6)式和(7)式,可以看出线极化奇点的情况可以用下面的关系表示:

(8)
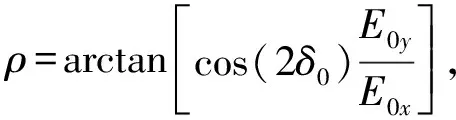
(9)
δ=2qπ(β=0.5qπ),q=±0,1,2,3…
(10)
因此,上面分析阐释了在生物组织图像形成极化奇点的一种可能性,并描述了这些奇点出现的主要机理.
2 进行双折射纤维物体场的极化结构的计算机模拟
为了测试上面关于生物组织物体场的极化非均匀结构形成的机制的模型,我们下面进行了计算机模拟.假设生物组织纤维的排列用二阶曲线描述:
A1x2+C1y2+2D1x+2E1y+F1=0.
(11)
这样物体场的极化态将在每点ri(x,y)连续变化.
这些近似为圆形的纤维束(N=55,见图1)被当做实际的物体使用,半径随着步长改变:ΔR=R+0.1R.同样,我们假设位相改变量坐标分布也具有圆形的特征(见图2).α(r),β(r)的具体值由式(7)决定,其中角度ρ有曲线在ri(x,y)切线方向和样本平面方向夹角的含义.
图3是椭圆率β(r)的坐标分布,其中生物组织图的极化态为{α0=450;β0=00}(图3(a))和{α0=00;β0=00}(图3(b)).椭圆率在图中是用三原色彩色标度图给出的.可以看出所有生物组织都是极化不均匀的.极化结构图像显示了椭圆极化态的连续变化,这种变化由单衰减(s轮廓,β(r)=0那条线)或双衰减(c点,β(r)=±π/4那条线)极化奇点的坐标分布决定.随着照射双折射纤维束的激光的极化态的改变,s轮廓的结构也在变化:封闭s轮廓的形成({α0=00;β0=00},图3(b));开放的s线和c线的形成(α0=450;β0=450,图3(a)).

图1 实际生物组织双折射纤维的方向结构图 图2 和空间位相改变量δ的依赖关系
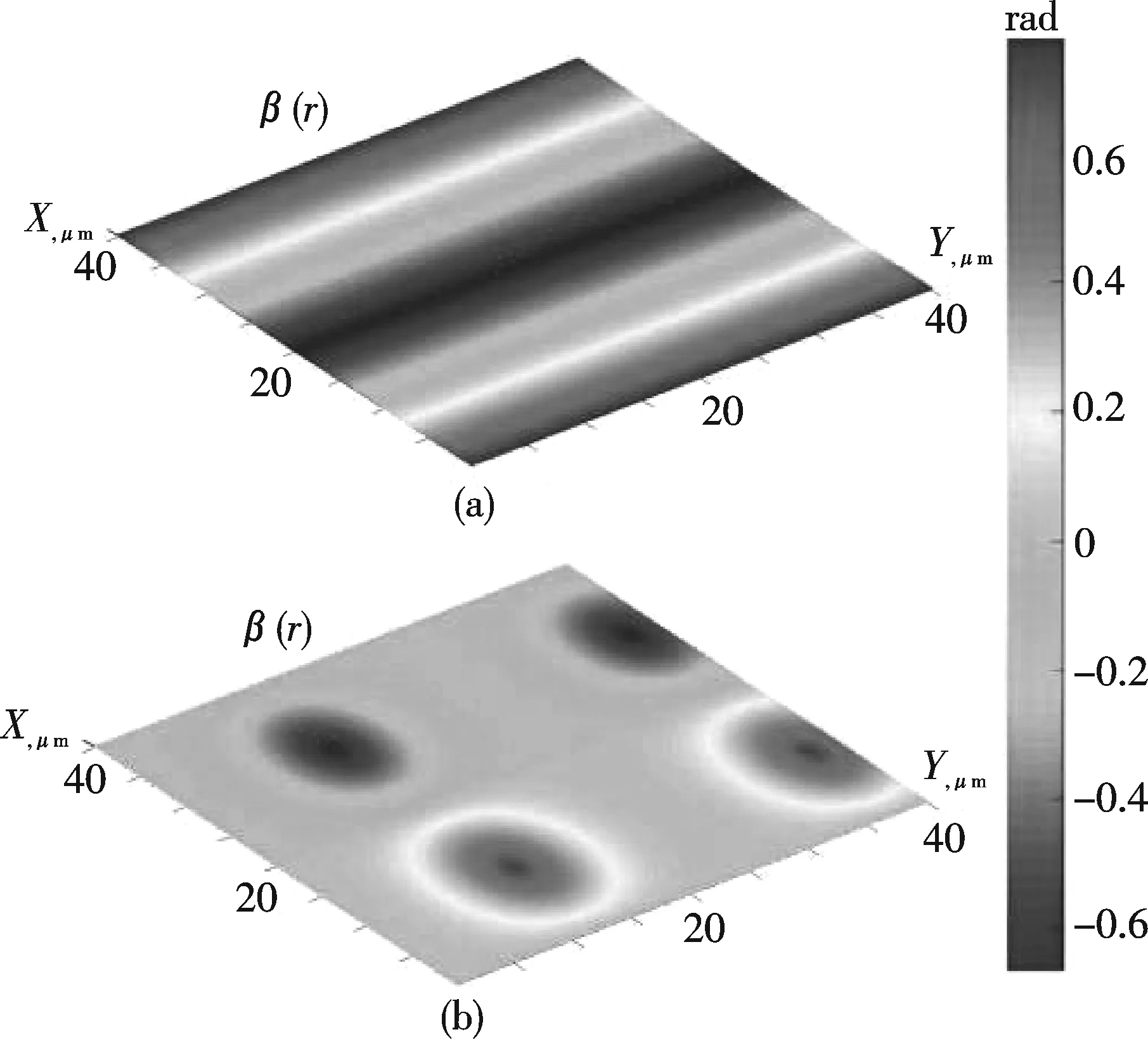
图3 实际生物组织图像光振荡的极化椭圆率β(r)的坐标分布
对比我们实际的双折射生物组织所有的s轮廓的结构,可以发现共同的拓扑特性:右旋的圆和椭圆偏振的点和线的区域被平面上线偏振的线与左旋的区域分开.
因此,我们可以说拓扑奇点方法在分析物体场极化结构形成机制和情形方面是正确的,这种物体场与纤维状的生物组织结构有关系.另一方面,不同极化点的物体场的相互关系的问题还没有得到解决.下面的部分将着手讨论这个问题,采用的是拓扑和关联的方法来描述极化非均匀物体场.
3 生物组织边界场的相互极化程度

{K(r,τ)}⟹{φ(r1,r2,τ)},
(12)

(13)
其中〈 〉代表时间平均,x和y后缀代表极化方向.
根据式(12)(13),相互极化程度(DMP)V2(r1,r2,τ)是决定极化场两不同极化点之间的联系的一个主要参量,这两个点的光强分别为I(r1,τ),I(r2,τ)[6].其可用如下形式表示[5]:
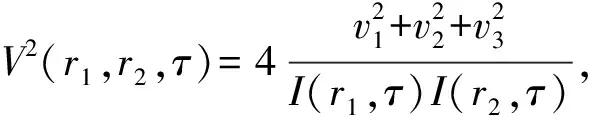
(14)
其中vi的由下面的关系定义:

(15)
光波在点r1,r2相互作用产生干涉,这些参量由干涉模式的差别决定.它们对应极化分析器的不同角度,在这里v1相当于分析器坐标的0°和90°,v2相当于分析器的45°和135°.参量v3应当用极化过滤器测量,即所谓的“四分之一波起偏器”.也就是说,第一种干涉模式对比是由四分之一波起偏器的快轴的0°和45°极化测量的,而当起偏器方向不变的情况下,第二种对比测量相当于快轴的135°.因此,我们可以看出相互极化程度V2(r1,r2,τ),表示了场在两不同点的极化特性间的相互关联.
表1提供了物体场两极化态不同的点的DMP值[7].第1行两点都是线极化状态.第2行是不同偏振方向的线极化态,并且描绘了两偏振态的相似程度.第3行描述了线极化和圆极化之间的关系.最后,第4行给出了正交的极化态的DMP值.可以看出,当两极化态是相同的时候|V2(r1,r2,τ)|2一直为1,线极化和圆极化之间是0.5,极化垂直的情况为0.

表1 完全相干场的DMP值例子
当极化相似的光波透过双折射生物组织层后,它的特性将会改变,这由光学各向异性的纤维的空间分布决定.在这部分中,我们考虑了用方向极化来测量生物组织图像(与用干涉效应来测量不同)[8],所用的方法是判断边界场两不同点的极化态和强度.
考虑两不同极化态的光振动:

(16)
其中δ1(r1),δ2(r2)表示r1,r2两点的场的两相互垂直分量Ex,Ey的相移.在生物组织图像完全相干光的情况下,式(2)的关联矩阵的形式成为:
(17)
考虑到式(16),我们从写(17)式为:
(18)
基于式(18),可以看出图像上给定两点的DMP值由下面的关系决定:
(19)
4 极化非均匀生物组织物体场的DMP值和奇点态的测量技术
生物组织物体场参量的空间分布的测量系统如图4所示.光源是准直了的氦氖激光(λ=0.632 8 μm,W=5.0 mw,直径为10 mm).极化是由3和5的1/4波片控制的,起偏器4调整极化光的角度和椭圆率,其中0°≤α0≤180°,0°≤β0≤90°.生物组织的极化图像是用显微样品7发射到CCD阵列9得到的,CCD的像素为800×600,CCD阵列可以为生物组织提供从2到200 μm的侧面范围测量.用起偏器8可以分析生物组织图像.

1.氦氖激光器;2.准直仪;波片;4、8.起偏器;6.研究的物体;7.显微样品;9.CCD摄影机;10.处理单元图4 生物组织样品偏振测定法光学系统
测量生物组织图像的奇点极化和DMP值的坐标分布技术的步骤如下:
1)生物组织图像的光强I(rm,n)坐标分布是由CCD阵列10测量的,不需要起偏器8.
2)插入起偏器8,传输轴的角度依次调整为Θ=0°,Θ=90°,分别测量光强I(0)(rm,n),I(90)(rm,n).
3)在Θ=0°→180°的范围内改变起偏器8传输轴的方向,测量每个像素点接收到的最大和最小光强Imax(rm,n),Imin(rm,n),同时测量对应的转动角度Θ(rm,n)|I(rm,n)=Imin.
4)生物组织的光振动极化态的坐标分布由下面的关系计算:
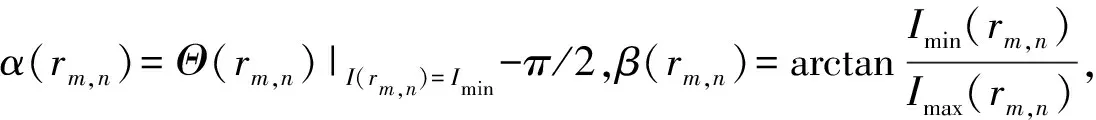
(20)
5)局域相移δ1(r1),δ2(r2)由下面的关系计算:

(21)
6)生物组织图像的DMP值由下面得关系,可直接用实验测量得出:
(22)
其中I(0)(ri),I(90)(ri)是在起偏器8的传输轴角度分别为0°和90°时生物组织图像的光强.
7)当β(rm,n)=0时为线极化奇点的图谱.
8)当β(rm,n)=π/4时为圆极化奇点图谱.
5 研究的物体和实验结果
最初,我们选择了一块几何厚度为100 μm的心肌组织和一束放射状的各向异性胶凝蛋白作为研究对象(见图5).这样选择是考虑到心肌组织的光线几何参量与上面分析的实际双折射生物组织(见图1)的本质相近.因此,通过计算机模型和实验得到的极化非均匀图像的拓扑结构的对比分析,我们可能得到最切合实际的结果.

“P”标记的是被研究极化拓扑结构区域图5 用同轴和交叉起偏器得到的心肌组织极化图像
图6(a)、图6(b)显示的分别为S型和C型极化奇点的拓扑分布,这是在心肌组织的P区域(见图5)在光源的状态为{α0=00;β0=00}的情况下实验得到的.其中S状态用黑色的点表示,右旋和左旋的C状态点分别用浅色和深色表示.

S状态用黑点标记;右旋的C点用浅点标记,左旋的C点用深点标记图6 心肌组织图像极化奇点(S轮廓)的拓扑分布
结果显示所有类型的S轮廓都在心肌组织的极化图像中出现.注意到图6(a)是实验得到的封闭S轮廓,这与图3(b)的模型的结构类似.图6(b)是开放S轮廓的拓扑结构,这与图3(a)的模型的结构类似.这是因为光学各向异性纤维在单极化光束的横截面上在极化角度α0方面是不同的.

S状态用黑点标记,右旋的C点用浅色点表示图7 真皮组织激光图像的极化奇点(S轮廓)的拓扑分布
用其他的有双折射岛状结构的生物组织做实验,也可以得到类似的结果,例如皮肤的真皮组织(见图7).这些数据都证实了闭合S轮廓是这类物体的典型特性.因此可以得出,生物组织物体场的拓扑极化结构的形成过程与散射场中闭合S轮廓的形成过程是一致的,前者的形成是由于光与双折射晶体机构的作用,后者的形成是由于不同极化态的波前统计相干[9-10].
另一方面,生物组织边界场的极化结构突出了其空间相移结构分布的特性.已经知道[11]方位和位相结果的结构网由生物组织的生理状态决定.因此,边界场拓扑奇点结构和生理正常和生理不正常的真皮组织的作用存在一个关系.
为了得到这种关系,我们研究了正常的和癌变的真皮组织.图8(a)是用交叉偏振光得到的真皮极化可视结构的显微图像.正常真皮组织的双折射结构是由随机取向的胶原蛋白纤维形成的,双折射为Δn≈10-3[11].纤维的半径为0.5到2 μm.癌变的真皮组织伴随着几何尺寸变大的胶原蛋白(图8(b)).图9是正常(图9(a))和癌变的(图9(b))真皮组织的椭圆率β(r)的坐标分布图.椭圆率β(r)的局域值是对图像抽样得到的,抽样间隔为Δri=1CCD像素.

图8 生理正常(a)和癌变(b)的真皮组织在交叉起偏器下的极化图像

图9 生理正常(a)和癌变(b)的真皮组织图像的极化椭圆率β(r)的坐标分布
结果显示两种真皮组织样本的边界场都是极化不均匀的.椭圆率β(r)的范围足够宽,跨度为-π/4→π/4,包括了极化奇点出现的椭圆率β(r)=0和β(r)=±π/4.癌变的真皮组织的图像极化机构的主要特点是β(r)的几何尺寸变大了(见图9(b)).这与增大尺寸的双折射胶原蛋白结构有关系.

图10 生理正常(a)和癌变(b)的真皮组织的单简并(浅色像素点)和双简并(深色像素点)极化奇点的坐标分布,这些分布是与真皮组织图像组合的

图11 生理正常(a)和癌变(b)的真皮组织的单简并和双简并极化奇点的坐标分布
在图10(a)、图10(b)中我们列出了极化奇点的坐标分布,浅色(代表线极化态)和深色(代表左旋和右旋的极化态)的点叠在对应的真皮图像上.除了简单的描述双折射真皮组织样本边界场的极化不均匀的特性,这个结果还可以作为研究这种不均匀性形成过程的基础.
对坐标分布β(r)=0和β(r)=±π/4的细节分析,可以看到边界场闭合“岛”性质的S轮廓(图11a,b).还可以看出健康真皮组织图像的S轮廓的范围是20到35μm,而癌变的真皮组织S轮廓的横截面积为7到15μm.
从物理的观点来看,从描述真皮组织结构中的双折射胶原蛋白的光学特性的建议模型分析,S轮廓的构成和光的圆偏折态得到了充分描述.首先,总可以找到纤维满足形成奇点(比较(8)-(11)式)的取向(ρ)和位相(δ=2πdΔn/λ). 其次,S轮廓的拓扑特性和几何尺寸由相干光的位相调制δ(r)决定.计算结果表明横截面直径为20μm的胶原蛋白纤维S轮廓的直径为14μm.这与健康真皮S轮廓尺寸的实验值相吻合.
癌变伴随着新形成的胶原蛋白的几何尺寸的增大.我们已经计算出当d=35μm时S轮廓的直径为9μm.考虑到这点,我们可以将处于前癌变态真皮组织图像观察到的S轮廓尺寸的减小与胶原蛋白相位调制深度的增加联系起来.
如果说分析极化奇点的坐标分布是从统计观点出发的,继而考虑真皮组织图所有极化态的相互关系式可能的.这些信息包含在被研究生物组织的DMP图像中.根据表1,DMP的值|V(Δrs)2|=0.5与S轮廓的截面尺寸一致(被线极化点包围的圆极化点)[5].这就是为什么Δrs被认为是S轮廓组的统计侧面几何尺寸.
因此,决定了生物组织图像的DMP坐标分布和计算出其自相关函数G(|V2|)后,我们可以得到S轮廓的平均侧面尺寸Δrs,这与确定值的G(|V2|)=0.5的半宽一致.图12(a)和图12(b)分别是正常的和癌变的真皮组织图像计算出来的|V2(r)|的坐标分布.;两种类型的真皮图像样品的|V2(r)|分布都是坐标不均匀的.它们是具有类似最高的极化态(|V2(r)|→1.0)和中间的DMP值(0.0≤|V2(r)|≤1.0).

图12 生理正常(a)和癌变(b)的真皮组织的DMP值分布
研究的真皮组织图像的DMP结构可以和不同的胶原蛋白的几何结构联系起来.具有更大几何范围的结构网的胶原蛋白纤维的有序性质包装材料,导致激光图像点上对应的极化态更大程度的自相似(|V2(r)|→1).移到其他的区域(例如不同结构取向的区域)伴随着极化态的改变,相应的将减小图像给定部分的点的DMP系数.然而,相干生物组织图上的点的DMP在自身取值范围内又变成了极值.
真皮组织的生理变化将带来胶原蛋白纤维的几何尺寸的变大和形成新的纤维增长方向的形态变化.从光学的观点来看,这个过程类似于照明真皮组织光源的极化方位角α0和光学各向异性结构的快轴方向ρ(rm,n)之间的角度间隔的增大.在相干真皮图像对应点,光振动的不同极化态α(rm,n),β(rm,n)形成.因此,DMP的模的波动增大.生理正常的图像中的|V2(r)|的自相关函数G(|V2|)对应的关联半径或者半宽Δrs将减小.图13描述了从正常(图13(a))的和癌变(图13(b))的真皮组织DMP坐标分布图像导出的自相关函数G(|V2|).数据明显的显示两种真皮组织的自相关函数的半宽和S轮廓的尺寸都很接近.

图13 DMP坐标分布的二维自相关函数(a,b),(c,d)对应自相关函数的三维图
因此,这个工作的要点就是关于拓扑和统计方法之间关联的一个陈述,这两种方法都是用来描述物体场极化不均匀的形成机制.也就是说,这种场的S轮廓的统计平均尺寸要和DMP的自相关函数的半宽一致.
6 结论
1) 在生物组织极化非均匀物体场的不同点都发现相关结构和奇点极化的拓扑状态相互关联:激光辐射与生物组织双折射结构之间的作用形成极化非均匀的边界场并出现奇点态,其拓扑结构与S轮廓相一致,S轮廓是由物体场在不同衍射区域的部分波前统计相干而形成的.DMP的自相关函数的半宽和S轮廓的统计平均尺寸一致.
2)当人体组织双折射结构的光轴取向和相移改变时,生物组织激光图像中的局域极化态之间的关系的结果可能在诊断中被利用.这些信息可能成为临床诊断生物组织癌变的基础.
参考文献:
[1] STOKES G G.On the composition and resolution of streams of polarized light from different sources[J].Trans Cambridge Phil Soc,1852(9):399-416.
[2] BORN M,WOLF E.Principles of optics[M].New York:Cambridge University Press,1999.
[3] USHENKO A G,PISHAK V P.Coherent-domain optical methods biomedical diagnostics[M].London: Kluwer Academic Publishers,2004.
[4] GORI F.Matrix treatment for partially polarized,partially coherent beams[J].Opt Lett,1998(23):241-243.
[5] ELLIS J,DOGARIU A.Complex degree of mutual polarization[J].Opt Lett,2004(29):536-538.
[6] BENOIT B MANDELBROT.The fractal geometry of nature[M].San Francisko:Freeman,1982.
[7] ANGELSKY O V,USHENKO A G,USHENKO Y A,etal.Polarization-correlation mapping of biological tissue coherent images [J].J Biomed Opt,2005,10(6):064025.
[8] MOKHUN I I.Optical correlation techniques and applications[M].Bellingham: SPIE Press,2007.
[9] BERRY M V,DENNIS M R.Polarization singularities in isotropic random vector waves[J].Pro Roy Soc,2001,A457:141-155.
[10] NYE J F.Lines of circular polarization in electromagnetic wave fields[J].Pro Roy Soc,1983,A389:279-290.
[11] FREUND I.Poincare vorties[J].Opt Lett,2001(26):1996-1998.

