双正交小波的谱半径及其应用

王国秋，杨梦云

(湖南师范大学数学与计算机科学学院,中国 长沙 410081)

正交小波变换是一能量守恒变换．无论是连续形式还是离散形式的小波变换，误差都是可控的．然而，作为小波理论的一个重要组成部分，双正交小波变换已不是一个能量守恒变换，虽然它是严格可逆的变换，但它的误差就不完全可控．因此，双正交小波变换的误差分析和控制就格外重要．

有关双正交小波变换的误差分析，涉及到框架上界的估计或小波变换算子的谱估计，到现在为止，并未见有关研究报道．小波函数大多是隐函数，所以直接对小波框架的界估计或连续小波变换算子的谱估计都有较大的困难．

双正交小波理论较优美，性能卓越．自从Cohen和Daubechies等的大作[1]问世后，双正交小波就逐渐为人们所认知，并在应用领域广泛使用[2-4]．当双正交小波由一个MRA生成时，我们采用了一种误差分析方法．本文的第一作者曾引进了2-循环矩阵的概念[5]，这个概念的意义在于能将Mallat算法[6]用严格的有限维矩阵来表示，从而可以借助代数学的成熟理论来研究小波中的一些问题．

1 双正交小波的谱半径

假定V=[v1,v2,…,vn-1,vn]是一个n维向量,这里n是正偶数．

定义一个算子σ:σ(V)=[vn-1,vn,v1,…,vn-3,vn-2]，则σn/2(V)=V．称σ是一个2-循环线性算子．

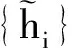
(1)

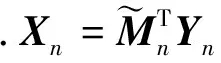
(2)

在Cohen和Daubechies等的理论指导下，产生了著名的9-7型双正交小波(简记为CDF97小波)[1]．然而，利用Cohen等的理论去构造偶数滤波器长度的双正交小波时，得到的小波可能既没有好的数学性质，也没有好的变换性能．例如，滤波器结构为8-8型(即高低通滤波器的长度均为8)的具有最高消失矩的双正交小波为：

低通滤波器(一半系数,对称)：{hi}={0.053 497 5,-0.087 225 8,-0.069 220 8,0.602 949}，

高通滤波器(一半系数,反对称)：{gi}={-0.022 817 9,0.037 203 8,0.133 432,-0.426 59}．

它们的构造思想是让一对高通滤波器分别具有5阶和3阶消失矩．这个小波简记为CDF88，可以验证这个小波的理论性质和应用表现都不理想．这一现象说明现有的双正交小波理论本身有待完善之处．

设λ是矩阵AAT的任意特征值，max(|λ|)就称为A的谱半径．

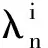
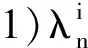
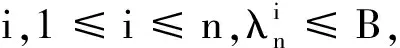
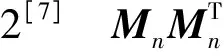
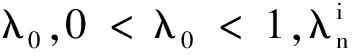
由引理可知，双正交小波不可能无限接近于一个正交系统．

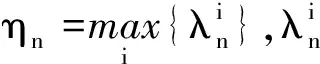
证由引理1的1)和3)，ηn为正且有上界，所以η的存在性显然．由引理3，ηn一定落在区间(λ0,1/λ0)之外，所以ηn>1/λ0，从而η≥1/λ0>1．

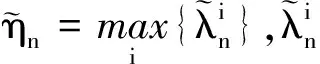
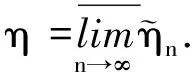
这个推论说明了当一个双正交小波给定后，有一个唯一的η与之对应．

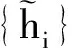
注若双正交小波由多分辨分析生成，则其滤波器和小波函数是等价的，所以上述定义适用于小波函数．称η为双正交小波的谱半径是因为ηn是Mn的谱半径，它的上极限与矩阵没有关系，而仅与这个双正交小波有关系．

谱半径的大小可以衡量一个双正交小波的正交程度，谱半径越小，反映双正交小波的正交程度更好．由于η是一个大于1的数，它离1越近，表示正交程度越好．但不能简单地说，谱半径越小越好，因为影响小波性能的因素很多，而谱半径大小只是其中关键的因素之一．

CDF88的谱半径的近似值和CDF97的谱半径的近似值见表1．CDF97的谱半径更接近1，所以它的正交程度更好一些．

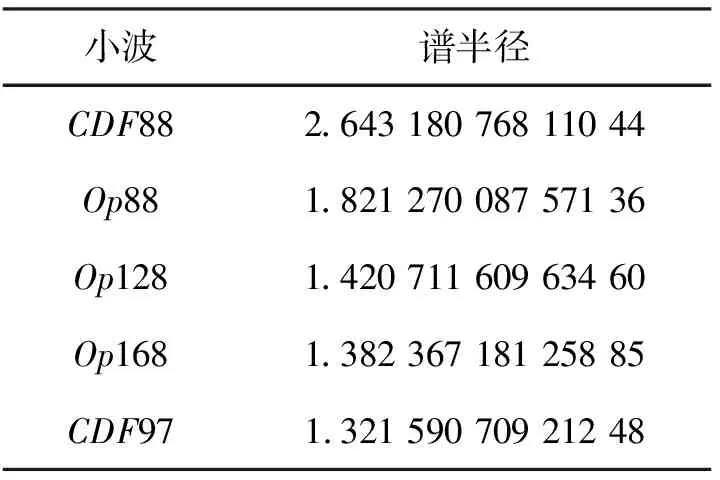
表1 不同小波的谱半径

2 基于最小谱半径的双正交小波类

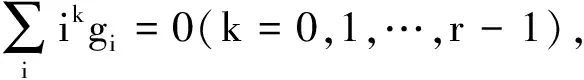
通过上面的讨论，希望得到min(η)，以便双正交小波系统是稳定的．因此，提出如下的一个小波类：

1)选取合适的小波结构，如奇数长或偶数长的，确定应用所需要的分解端的滤波器的长度．

2)根据分解端高通滤波器的长度L决定消失矩的阶数，一般偶数长L的最高消失矩为L/2+1阶，奇数长L的最高消失矩为(L+1)/2阶．同时，重构端高通滤波器也给予一定的消失矩条件．

3)选取满足min(η)的双正交小波．

我们称这个小波类为基于最小谱半径的双正交小波类．

具有偶数长滤波器的双正交小波中性能优异者并不多见．下面给出8-8型、12-8型和16-8型最优小波各一个，它们的分解端高通滤波器的长度都为8，消失矩都为5阶，重构端高通滤波器的消失矩的阶数不作限制可设为1阶矩．注意，10-8型、14-8型小波不存在．之所以给出3组小波，是因为在8-8型和12-8型里的最优解的谱半径过高，要想进一步最小化谱半径，就必须增加参数，故需加长滤波器的长度．

8-8型(Op88):

低通滤波器(一半系数,对称)：{hi}={0.099 856 2,-0.197 88,0.110 494,0.487 53}，

高通滤波器(一半系数,反对称){gi}={-0.030 686 9,0.060 810 8,0.125 563,-0.465 935}．

12-8型(Op128)：

低通滤波器(一半系数，对称)：{hi}={0.0169 69,-0.036 622,0.103 044,-0.112 219,0.049 022 9,0.479 804}，

高通滤波器(一半系数,反对称)：{gi}={-0.037 121 7,0.080 115 2,0.119 128,-0.498 109}．

16-8型(Op168)：

低通滤波器(一半系数,对称)：{hi}={0.007 204 13,-0.015 614 2,-0.005 060 77,0.057 583 1,0.009 750 06,-0.091 724 8,0.068 464 5,0.469 398}，

高通滤波器(一半系数,反对称)：{gi}={-0.037 533,0.081 348 9,0.118 717,-0.500 165}．

它们的谱半径见表1．Op88和Op128的图像较CDF88虽有改善，但分解端的尺度函数和小波函数的图像效果仍不理想，均类似于CDF88，说明5阶的高消失矩要求有些勉强，因此在给定的结构里达不到希望的谱半径．而Op168的图像已非常光滑(见图1)，可见谱半径的大小与图像的光滑性有某种必然的内在关系．

图1 Op168小波，其中，(a)和(c)是尺度函数对；(b)和(d)是小波函数对

3 实验分析

SPIHT算法[4]是一个优秀的图像压缩编码算法，它最大限度地利用了小波变换的特性，所以SPIHT算法也是全世界公认的测试小波性能的有效手段之一．我们采用SPIHT算法来测试所得到小波基的性能．在SPIHT算法里，我们采用Huffman熵编码算法，小波分解次数都是6次，一律采用周期延拓处理边界．重建信号与原始信号的误差采用峰值信噪比(PSNR)来衡量．实验图像为常用的具有两种典型分布的512×512的Barbara和Lena测试图．试验结果在表2和表3中．在表2和表3中，第一列为图像的压缩比(如“1∶4”表示压缩图像与原始图像的存储空间比为1∶4，其他类似)，表中的数据为PSNR(dB)．

实验数据表明，Op88与CDF88的结构相同，但Op88性能有很大的改善，说明最小化谱半径是有效的．就4组小波(CDF88，Op88，Op128，Op168)而言，它们的谱半径是逐渐降低的，但它们的性能大体上是增加的．对于Op168，就两幅测试图，它的压缩编码能力几乎在各个码率上都超过了CDF97的，尤其对复杂纹理图像，在中等码率下，具有超过0.4 dB的PSNR的优势，这一优势在图像压缩编码里是不可忽略的，尤其对于复杂图像，解码图像的质量提高是非常困难的．所以，本文的结果无疑给研究者构造更好的小波带来了希望．

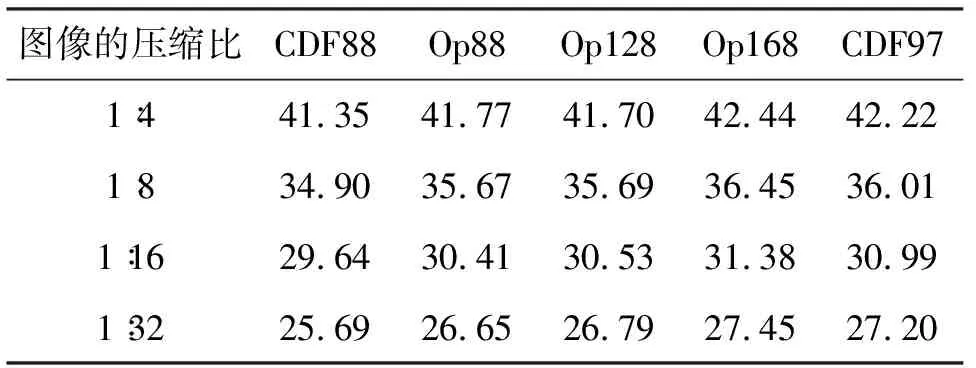
表2 Barbara测试结果

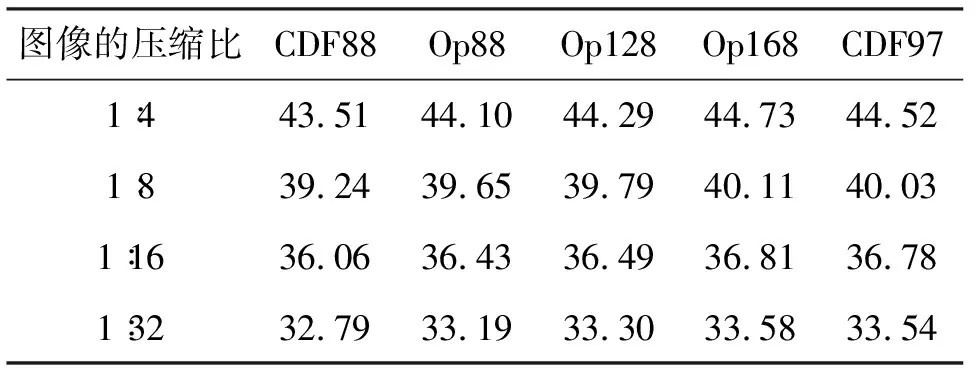
表3 Lena测试结果

4 结束语

本文提出的双正交小波的谱半径是一个重要概念.用这个概念能定量地衡量一个双正交小波的正交程度的高低．在高消失矩条件下，最小化谱半径才能凸显双正交小波的优势．

参考文献：

[1] COHEN A,DAUBECHIES I,FEAUVEAU J C.Biorthogonal bases of compactly supported wavelets[J].Pure Appl Math,1992,45:485-560.

[2] VILLASENOR J D.Wavelet filter evaluation for image compression[J].IEEE Tran Image Process,1995,4(8):1053-1059.

[3] TAUBMAN D.High performance scalable image compression with EBCOT[J].IEEE Tran Image Process,2000,9(7):1158-1170.

[4] SAID A,PEARLMAN W.A new fast and efficient image code based on set partitioning in hierarchical trees[J].IEEE Trans Circuits System Video Tech,1996,6(3): 243-249.

[5] WANG G Q.Matrix methods of constructing wavelet filters and discrete hyper-wavelet transforms[J].Opt Eng,2000,39(4):1080-1087.

[6] MALLAT S.A theory for multiresolution signal decomposition: the wavelet representation[J].IEEE Trans Pattern Anal Mach Intell,1989,11(7): 674-693.

[7] WANG G Q,YUAN W W.Optimal model for biorthogonal wavelet filters[J].Opt Eng,2003,42(2): 350-356.

[8] 邹庆云,王国秋.离散超小波变换下双正交小波谱分析[J].数学进展,2008,37(3):332-336.