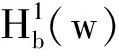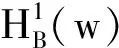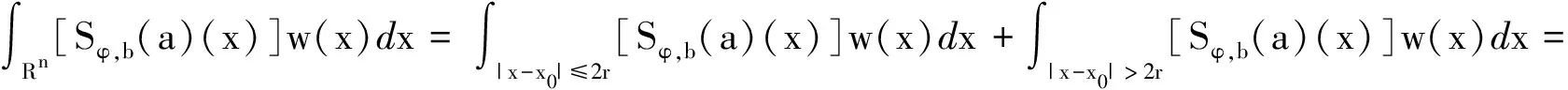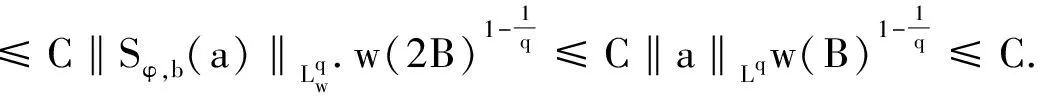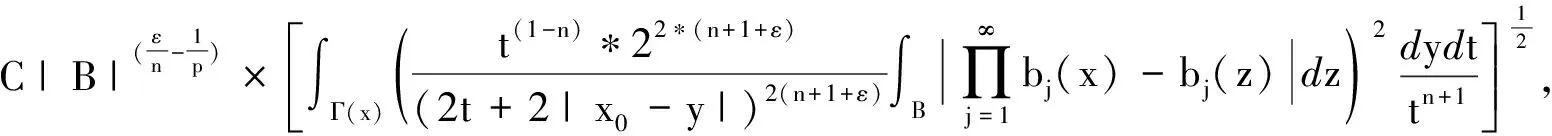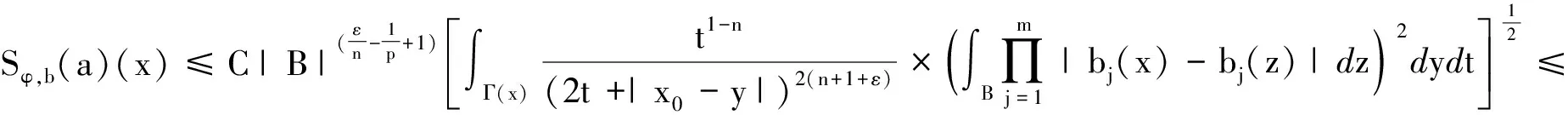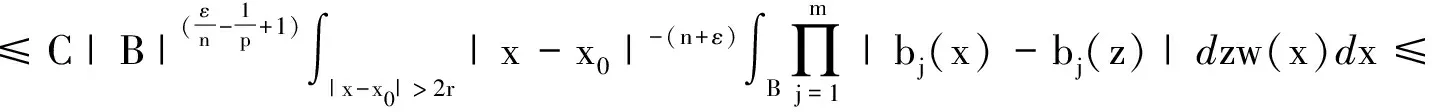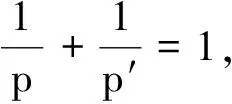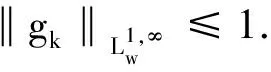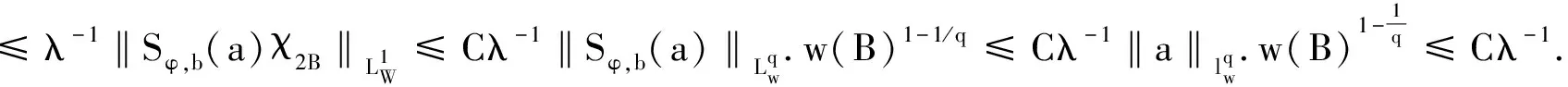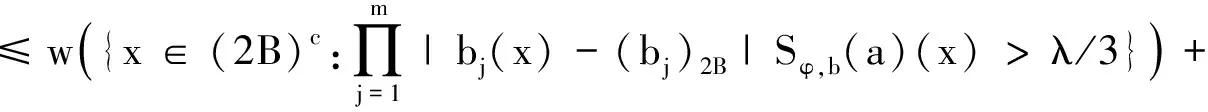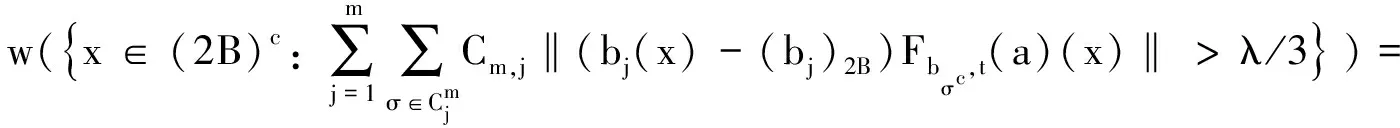Littlewood-Paley算子的多线性交换子在一类Block-Hardy空间上的加权有界性
曾甲生
(湖南商学院信息学院,湖南 长沙 410205)
1 引言
Littlewood-Paley 算子作为分析数学中一个十分重要的积分算子,本文提出了Littlewood-Paley 算子相关联的多线性交换子的概念,并将研究它们在Hardy型空间中的有界性.我们先给出一些记号和定义.
设B=B(x0,r)表示中心为x0半径为r的球.给定B和局部可积函数f,令
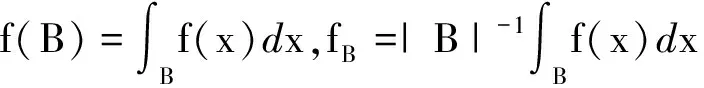
称f属于BMO,若f#∈L∞并且定义‖f‖BMO=‖f#‖L∞.
设m为正整数,bj(x)(j=1,…m)为可积函数,对任意的正整数1≤j≤m,我们记
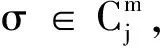
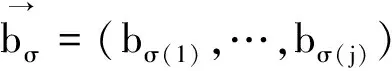
本文将要研究的Littlewood-Paley算子定义如下:
令ε≥0以及确定一个函数φ,满足如下条件:
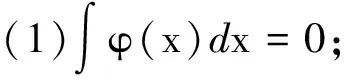
(2)|φ(x)|≤C(1+|x|)-(n+ε);
(3)|φ(x+y)-φ(x)|≤C|y|ε(1+|x|)-(n+1+ε).
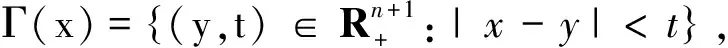
设m为正整数,bj(x)(j=1,…m)为可积函数,则由Littlewood-Paley算子和bj(x)生成的多线性交换子定义为:
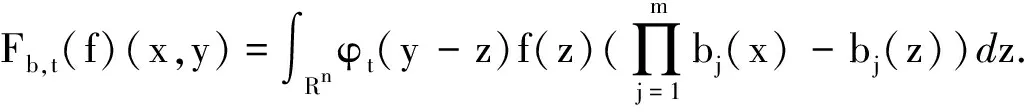
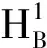
定义1设m为正整数,bj(x)(j=1,…m),w(x)为可积函数并且w(x)∈A1(即Mw(x) (i)suppa(x)⊂B=B(x0,r); 有了这两个定义,下节我们将叙述并证明本文的结论. 定理1的证明我们只需证明存在常数C>0,使对任意(w,b)原子a(x)满足 事实上,设a(x)为(w,b)原子,suppa(x)⊂B=B(x0,r),记 设给定q>1,运用Hölder’s不等式,以及Sφ,b(f)(x)的Lq-有界性[5]可得: 又可知 注意到2t+|x0-y|>2t+|x0-x|-|x-y|>t+|x0-x| 当|x-y| 由此可知 所以 对上面的估计,因为w∈A1,w满足逆Hölder’s不等式,对于任意的球Q,和某个1 所以上式会小于或等于 定理1证毕. 在证明定理2之前,首先阐述一个引理[7]: 定理2的证明根据引理,只要证明存在一个常数C,对于任意的w-原子a,suppa(x)⊂B=B(x0,r),有下式成立, 由 w({x∈(2B)c:Sφ,b(a)(x)>λ})≤w({x∈2B:Sφ,b(a)(x)>λ})+ w({x∈(2B)c:Sφ,b(a)(x)>λ})=Ⅰ+Ⅱ. 对于Ⅰ,根据Sφ,b(a)的Lq(q>1)有界性,可得: 因而,有 与定理1的证明类似,我们可以证得, 对于Ⅱ2,我们同理可得到: 对于Ⅱ3,由Hölder’s不等式,以及μΩ的Lq有界性,我们可得: 合并上述证明过程,可得: 定理2得证. 参考文献: [1] ALVAREZ J.Continuity properties for linear commutators of Calderon-Zygmund operators[J].Collect Math,1998,49(1):17-31. [2] GARCIA-CUERRA J.Weighted norm inequalities and related topics[M].Amsterdan:North-Holland Math Studies,1985. [3] KOMORI Y.Weighted hardy spaces estimates for commutators of singular integral operators[J].Far East J Math Sci,2001,3(6):889-898. [4] LIU L Z.Weighted weak type (H1,L1) estimates for commutators of Littlewood-Paley operators[J].Indian J Math,2003,45(1):71-78 . [5] LIU L Z.Continuity for commutators of Littlewood-Paley operators on certain Hardy spaces[J].J Korean Math Soc,2003,40(1):41-60. [6] PEREZ C.Sharp weighted estimates for multilinear commutators[J].J London Math Soc,2002,65(4):672-692. [7] STEIN E M.On convergence of poisson integrals[J].Trans Amer Math Soc,1969,140(1):35-54.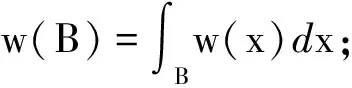
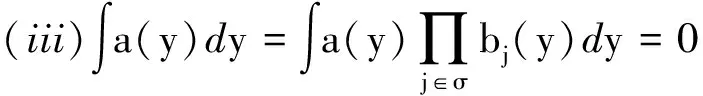
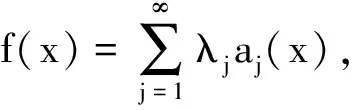
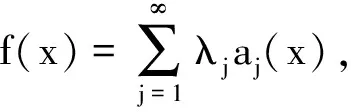
2 定理及其证明